7-3 プレートテクトニクスの幾何学:球面上のプレート
プレートの移動とオイラー回転: プレートテクトニクスを球面上で扱うときは,プレートは球殻状の板となります.球殻状の板が球面上を移動するとき,その運動はオイラー極と呼ばれる固定点の回りの回転運動で表わされ,これをオイラーの定理といいます.移動が複数回に渡って異なるオイラー極の回りに回転した場合も,全体としての移動を表わす1回のオイラー回転が存在します.
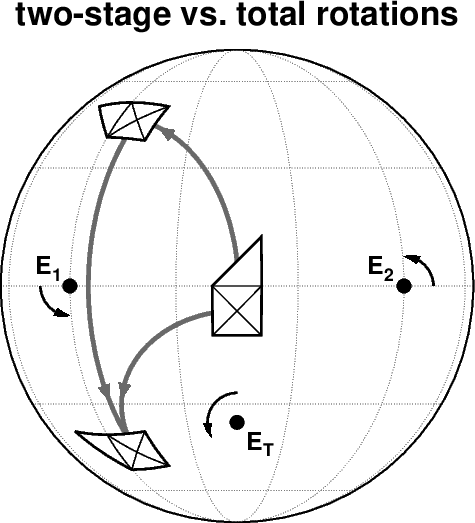
右図は連続した2回の段階的オイラー回転と1回の全回転が同等となる例です.オイラー極 E1 と E2 は赤道上で 90° 離れており,赤道付近のプレートが E1 の回りに 90° 回転して北半球に移動し,その後 E2 の回りに 90° 回転して南半球に移動しました.これと同じ結果が南半球に位置するオイラー極 ET の回りの 120° の回転で得られます.なお,回転の角度は地球中心から見て右ねじの進む方向,即ち地球外から見て反時計回りを正とします.
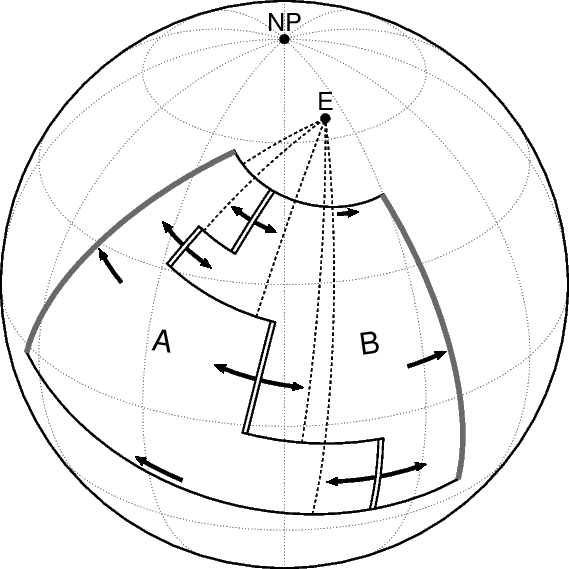
左図はオイラー回転による海洋底拡大の模式図です.二重線,実線,太い灰色の実線はそれぞれ海嶺,トランスフォーム断層,海溝で,プレート A と B がオイラー極 E の回りにそれぞれ時計回りと反時計回りに回転しています.点線は各トランスフォーム断層の走行に垂直な大円でオイラー極で交わります.また,プレートの移動速度はオイラー極から離れるに従い大きくなります.ある地点の移動速度(回転速度)は,その地点とオイラー極との角距離を \(\delta\) として \(\sin\delta\) に比例し,オイラー極から 90° の地点で最大です.
実際の観測では,トランスフォーム断層に垂直な大円は理論通りに1点で交わることは稀ですので,最小二乗法により誤差が最小になるようオイラー極を求めます.オイラー極の決定にはその他に,トランスフォーム断層沿いの地震のスリップベクトルを使用したり,地磁気縞状異常の等年代線から求まる各地の移動速度を \(\sin\delta\) 則に当てはめるなどがあります.なお,図ではプレートの相対速度ベクトルに垂直に海嶺や海溝を描いてあるので,これらの走行の延長線もオイラー極で交わりますが,実際には海嶺や海溝は速度ベクトルに垂直でないことが多く,これらはオイラー極の決定には使用されないようです.
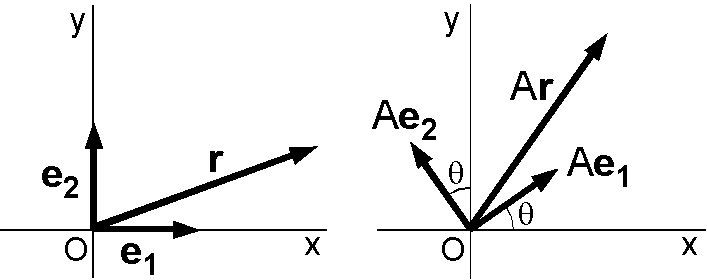
2次元の回転行列: 線形代数ではベクトルの回転は線形変換であり,行列で表わします.右図は2次元の回転行列を求める手順です(他の方法は → ここです).ベクトル \({\bf r}=(x,y)\) は基底ベクトル \({\bf e_1}=(1,0)\) と \({\bf e_2}=(0,1)\) を用いると, \begin{equation} {\bf r} = x{\bf e_1} + y{\bf e_2}, \label{eq01} \end{equation} と表わせます. \(A\) を回転の線形変換とすると,角度 \(\theta\) 回転後のベクトル \({\bf r'}=(x',y')\) は, \begin{equation} {\bf r'} = A{\bf r} = A(x{\bf e_1} + y{\bf e_2}) = xA{\bf e_1} + yA{\bf e_2}, \label{eq02} \end{equation} となります.また,回転後の基底ベクトル \(A{\bf e_1}=(\cos\theta,\sin\theta)\) と \(A{\bf e_2}=(-\sin\theta,\cos\theta)\) は, \begin{equation} A{\bf e_1} = \cos\theta{\bf e_1} + \sin\theta{\bf e_2}, \quad A{\bf e_2} = -\sin\theta{\bf e_1} + \cos\theta{\bf e_2}, \label{eq03} \end{equation} のように \({\bf e_1}\) と \({\bf e_2}\) を用いて表わされます. (3) を (2) に代入して, \[ {\bf r'} = [(\cos\theta)x - (\sin\theta)y]{\bf e_1} + [(\sin\theta)x + (\cos\theta)y]{\bf e_2}, \] となります. \({\bf r'} = x'{\bf e_1} + y'{\bf e_2}\) ですので, \[ x' = (\cos\theta)x - (\sin\theta)y, \quad y' = (\sin\theta)x + (\cos\theta)y, \] の関係を得ます.これをベクトルの縦表記で表わすと, \[ \left(\begin{array}{c} x' \\ y' \end{array}\right) = \left(\begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array}\right) \left(\begin{array}{c} x \\ y \end{array}\right), \] ですので,回転行列は次のようになります. \begin{equation} A = \left(\begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array}\right). \label{eq04} \end{equation} この行列は回転後の基底ベクトル \(A{\bf e_1}\) と \(A{\bf e_2}\) を縦表記にして横に並べた形になっています.一般に,回転後の基底ベクトルを \({\bf f_1}\) と \({\bf f_2}\) で表わすと回転行列は次にように表わせます. \[ A = \left(\begin{array}{cc} {\bf f_1} & {\bf f_2} \end{array}\right) = \left(\begin{array}{cc} f_{1x} & f_{2x} \\ f_{1y} & f_{2y} \end{array}\right). \]
3次元の回転行列: 3次元の場合も同様に,回転後の基底ベクトル \(A{\bf e_1}\), \(A{\bf e_2}\), \(A{\bf e_3}\) をそれぞれ \({\bf f_1}\), \({\bf f_2}\), \({\bf f_3}\) とおくと,回転後のベクトル \({\bf r'}\) は, \[ {\bf r'} = A{\bf r} = A(x{\bf e_1} + y{\bf e_2} + z{\bf e_3}) = x{\bf f_1} + y{\bf f_2} + z{\bf f_3}, \] ですので, \({\bf r'}\) や \({\bf r}\) を縦表記として,ベクトル \({\bf r}\) の回転は次式で表わせます. \begin{equation} {\bf r'} = \left(\begin{array}{ccc} {\bf f_1} & {\bf f_2} & {\bf f_3} \end{array}\right) {\bf r}. \label{eq05} \end{equation} これを成分で表示すると次のようになります. \begin{equation} \left(\begin{array}{c} x' \\ y' \\ z' \end{array}\right) = \left(\begin{array}{ccc} f_{1x} & f_{2x} & f_{3x} \\ f_{1y} & f_{2y} & f_{3y} \\ f_{1z} & f_{2z} & f_{3z} \end{array}\right) \left(\begin{array}{c} x \\ y \\ z \end{array}\right). \label{eq06} \end{equation}
3次元直交座標系でベクトルを1つの座標軸の回りに回転する場合,回転後の基底ベクトルは下図から分かりますので,回転行列の導出は容易です.
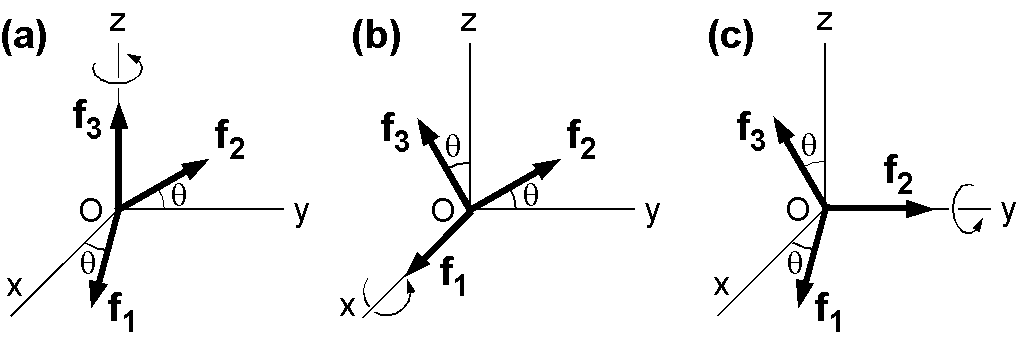
例えば,図(a)の z 軸の回りの回転では, \[ {\bf f_1} = (\cos\theta, \sin\theta, 0), \quad {\bf f_2} = (-\sin\theta, \cos\theta, 0), \quad {\bf f_3} = (0, 0, 1), \] ですので,回転行列 \(A_z\) は式(6)より, \[ A_z = \left(\begin{array}{ccc} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{array}\right), \] となります.同様にして, x 軸と y 軸の回りの回転行列は次のようになります. \[ A_x = \left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{array}\right), \quad A_y = \left(\begin{array}{ccc} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{array}\right). \]
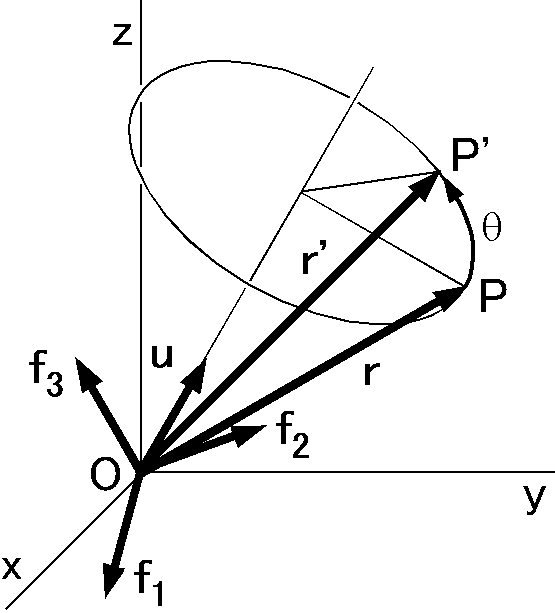
任意の軸の回りの回転: 右図はベクトル \({\bf r}\) が,単位ベクトル \({\bf u}\) で表わされる任意の軸の回りに角度 \(\theta\) 回転する様子を示します.この場合,回転後のベクトル \({\bf r'}\) は \({\bf u}\) と \({\bf r}\) を用いて次のロドリゲスの回転公式で表わされます(式の導出は → ここです). \begin{equation} {\bf r'} = (1-\cos\theta)({\bf r}\cdot{\bf u}){\bf u} + \cos\theta{\bf r} + \sin\theta({\bf u}\times{\bf r}). \label{eq07} \end{equation} ここに, \(\cdot\) と \(\times\) はそれぞれベクトルの内積と外積を表わします.この式の \({\bf r}\) に回転前の基底ベクトル \({\bf e_1}\), \({\bf e_2}\), \({\bf e_3}\) を代入すると, \({\bf r'}\) として回転後の基底ベクトル \({\bf f_1}\), \({\bf f_2}\), \({\bf f_3}\) が求まります.これらの回転後の基底ベクトルと式(6)から,任意の軸の回りの回転行列は次式となります. \begin{equation} \left(\begin{array}{lll} \scriptsize{u_xu_x(1-\cos\theta)+\cos\theta} & \scriptsize{u_xu_y(1-\cos\theta)-u_z\sin\theta} & \scriptsize{u_xu_z(1-\cos\theta)+u_y\sin\theta} \\ \scriptsize{u_yu_x(1-\cos\theta)+u_z\sin\theta} & \scriptsize{u_yu_y(1-\cos\theta)+\cos\theta} & \scriptsize{u_yu_z(1-\cos\theta)-u_x\sin\theta} \\ \scriptsize{u_zu_x(1-\cos\theta)-u_y\sin\theta} & \scriptsize{u_zu_y(1-\cos\theta)+u_x\sin\theta} & \scriptsize{u_zu_z(1-\cos\theta)+\cos\theta} \end{array}\right). \label{eq08} \end{equation}
有限回転の非可換性: 回転角度が微小ではない有限回転を,異なる軸の回りに2回行うとき,回転の順序を逆にすると結果は異なります.この有限回転の非可換性は線形代数で行列の積が一般には交換法則を満たさないことから分かります.よく挙げられる例は,机上に寝かせた本を直交する2方向に 90° 回転させる(起こす)とき,順番を逆にすると結果が異なることです.ここでは,冒頭に示したプレートの連続する2回のオイラー回転を逆にした例を下図に示します.
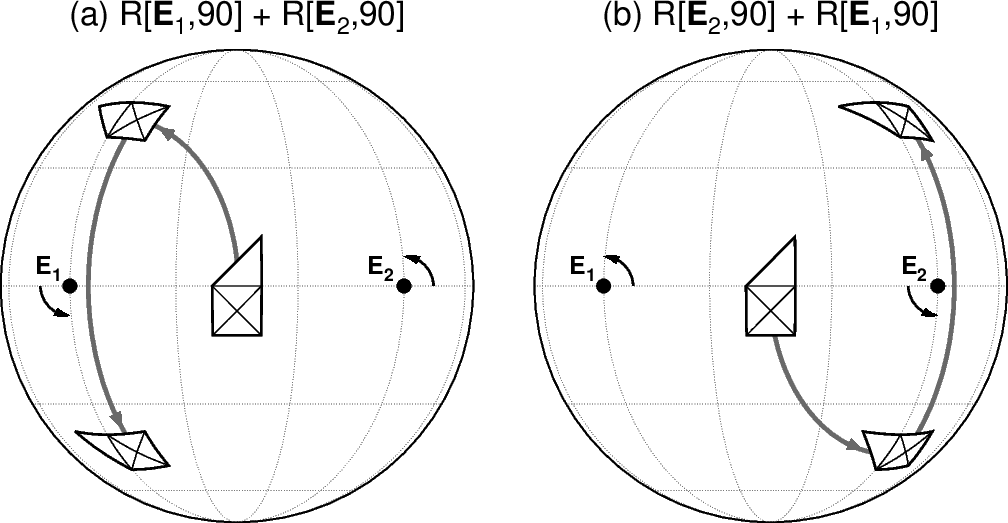
図 (a) の R[\({\bf E}_1\),90] + R[\({\bf E}_2\),90] は,オイラー極 \({\bf E}_1\) の回りに 90° 回転した後にオイラー極 \({\bf E}_2\) の回りに 90° 回転するという記号です.図 (b) はその逆ですが,プレートの最後の位置が異なります.また,冒頭の例では (a) の2回連続回転が次のように1回の全回転に等しいことを示しました.
しかし,これは全回転のオイラー極がベクトルの和で求まるということではありません.このことは有限回転の非ベクトル性とも言われています.なお,全回転のオイラー極とその回転角は,回転行列の積を電卓などで計算すれば,その成分から決定できます(計算式の詳細は → ここです).
上の回転の記号に添え字を加えて \(_AR_B[{\bf E},\theta]\) を,プレート A を固定してプレート B を現在の位置から過去のある時点の位置まで戻すときの回転(オイラー極 \({\bf E}\) と回転角 \(\theta\))を表わすとし,これを全復元回転といいます(通常は年代の範囲を \(_A^0R_B^t\) として添えますがここでは省略します).
いま,3つのプレート A, B, C があり, A を固定したときの C の全復元の回転を求めたいが, A と C の間には等年代線などがなくオイラー極が決められないとします.しかし, B に対する C の全復元回転 \(_BR_C[{\bf E}_1,\theta_1]\) と A に対する B の全復元回転 \(_AR_B[{\bf E}_2,\theta_2]\) は分かっているとします.そこで, A に対する C の全復元回転をプレート B を介して求めますが,その際の回転の順序は重要で次の通りです. \begin{eqnarray*} _AR_C[{\bf E},\theta] & = & _BR_C[{\bf E}_1,\theta_1] + {_A}R_B[{\bf E}_2,\theta_2], \\ & \not= & _AR_B[{\bf E}_2,\theta_2] + {_B}R_C[{\bf E}_1,\theta_1]. \end{eqnarray*}
2プレート間について,現在から過去の時点までの全復元回転が求まっても,実際には1回の回転ではなく異なるオイラー極で段階的に回転したことも考えられます.この途中の2つの年代間の回転を段階回転といいます.段階回転を求め過去のプレート配置を復元することはプレートテクトニクスの重要なテーマですが,有限回転の非可換性や非ベクトル性のためにその作業は大変複雑です.
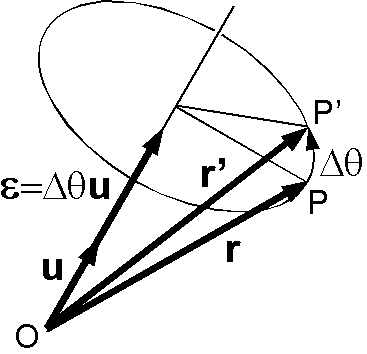
ベクトルとしての無限小回転: 有限回転に対して無限小回転はベクトルとして扱えます.図のようにベクトル \({\bf r}\) が微小角度 \(\Delta\theta\) 回転したとします.回転後の \({\bf r'}\) は式 (7) から求まりますが,その際に次のように近似します. \[ \cos\Delta\theta \approx 1, \quad \sin\Delta\theta \approx \Delta\theta. \] 近似後の式 (7) は次のようになります. \[ {\bf r'} = {\bf r} + \Delta\theta({\bf u}\times{\bf r}). \] ここで,単位ベクトル \({\bf u}\) の方向で大きさが \(\Delta\theta\) の無限小回転ベクトル, \[ \boldsymbol{\epsilon} = \Delta\theta{\bf u}. \] を導入します(一般に,回転ベクトル \({\bf v}\) はその向きが回転軸を,大きさ \(|{\bf v}|\) が回転角度を表わします).この無限小回転ベクトル \(\boldsymbol{\epsilon}\) を用いると式 (7) の近似式は次のようになります. \begin{equation} {\bf r'} = {\bf r} + \boldsymbol{\epsilon}\times{\bf r}. \label{eq09} \end{equation} いま,ベクトル \({\bf r'}\) が別の回転軸の回りに微小角度 \(\Delta\theta'\) 回転したとすると,回転後は, \[ {\bf r''} = {\bf r'} + \boldsymbol{\epsilon'}\times{\bf r'}, \] で表わされますが,これに式 (9) を代入すると, \begin{eqnarray*} {\bf r''} & = & {\bf r} + \boldsymbol{\epsilon}\times{\bf r} + \boldsymbol{\epsilon'}\times({\bf r} + \boldsymbol{\epsilon}\times{\bf r}), \\ & = & {\bf r} + \boldsymbol{\epsilon}\times{\bf r} + \boldsymbol{\epsilon'}\times{\bf r} + \boldsymbol{\epsilon'}\times(\boldsymbol{\epsilon}\times{\bf r}), \end{eqnarray*} となりますが,高次の項を省略して近似すると,次式を得ます. \[ {\bf r''} = {\bf r} + (\boldsymbol{\epsilon} + \boldsymbol{\epsilon'})\times{\bf r}. \] この式は式 (9) と同じ形をしており, \(\boldsymbol{\epsilon}\) と \(\boldsymbol{\epsilon'}\) で表わされる無限小回転を続けて行うと,それらのベクトル和の1回の無限小回転と同等であることを示します.また,明らかに交換法則も成り立ちます.
角速度ベクトル: ベクトル \({\bf r}\) が微小時間 \(\Delta t\) の間に微小角度 \(\Delta\theta\) 回転したとすると \(\Delta\theta/\Delta t\) はその時点の瞬間の角速度となります.そこで,次の角速度ベクトルを定義します. \[ \boldsymbol{\omega} = \boldsymbol{\epsilon}/\Delta t = (\Delta\theta/\Delta t){\bf u}. \] 角速度ベクトル \(\boldsymbol{\omega}\) はその方向が回転軸を,大きさが角速度を表わします.このように定義された角速度ベクトルは無限小回転ベクトルと同様に,ベクトルとしての分解や合成が可能で,交換法則も成り立ちます.この角速度ベクトル \(\boldsymbol{\omega}\) を用いて,微小時間 \(\Delta t\) の間のベクトル \({\bf r}\) の変位 \(\Delta{\bf r}\) は式 (9) より, \[ \Delta{\bf r} = {\bf r'} - {\bf r} = \boldsymbol{\omega}\times{\bf r}\Delta t, \] と表わせますので,ベクトル \({\bf r}\) の回転速度(線速度) \({\bf v}\) は次式となります. \begin{equation} {\bf v} = \frac{d{\bf r}}{dt} = \boldsymbol{\omega}\times{\bf r}. \label{eq10} \end{equation}
プレート運動と無限小回転: プレートのオイラー回転は最近百万年程度については,無限小回転として扱います.プレートの多くは百万年当たり 1° 前後で回転するので, 1° は 0.017453 ラジアンですが, sin(1°) は 0.017452, cos(1°) は 0.99985 で,式 (9) を導いた近似条件を満たします.そのため,プレート運動は主に角速度ベクトルを用いて解析します.
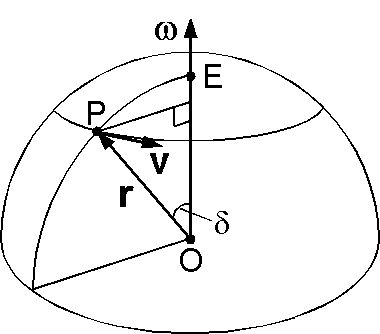
プレートが角速度 \(\omega\) で回転しているとき,オイラー極 E から角距離 \(\delta\) 離れた地点の移動速度 \(v\) は右図のように式 (10) を用いて次式となります. \begin{equation} v = \omega r\sin\delta. \label{eq11} \end{equation} オイラー極は主にトランスフォーム断層の走行に直交する複数の大円の交点から求め,角速度は地磁気異常の等年代線から求めた複数の地点の移動速度を式 (11) に合うように決定します.一旦,オイラー極と角速度が決まるとプレート上のあらゆる地点の移動速度が求まります.角速度ベクトルはオイラー極 E の緯度 \(\lambda\),経度 \(\phi\),角速度 \(\omega\) を用いて次のように表わします. \[ \boldsymbol{\omega} = (\lambda, \phi, \omega) \] 回転の向きは,右ねじがベクトルの向きに進むときのそれで,地球外から見て反時計回りです.この極に対して時計回りの回転は,対極をオイラー極として, \(\boldsymbol{\omega}=(-\lambda,\phi+180,\omega)\) とします.角速度を負として \((\lambda,\phi,-\omega)\) (\(\omega\) > 0) の表現も構いませんが前者が一般的です.また,地球中心が原点で赤道上で 0°E と 90°E 方向を x 軸と y 軸,自転軸の北極方向を z 軸とした地心直交座標系を用いて,次のように表わすこともできます.この表現は数値の計算に向いています. \begin{equation} \boldsymbol{\omega} = \left(\begin{array}{c} \omega_x \\ \omega_y \\ \omega_z \end{array}\right) = \left(\begin{array}{c} \omega\cos\lambda\cos\phi \\ \omega\cos\lambda\sin\phi \\ \omega\sin\lambda \end{array}\right). \label{eq12} \end{equation}
プレート運動の角速度はあくまで2プレート間の相対角速度です.そのため,プレート A に対するプレート B の角速度は \(_A\boldsymbol{\omega}_B\) と表わします(添字を逆にする教科書もあります).3つのプレート A, B, C があるとき, A に対する C の角速度 \(_A\boldsymbol{\omega}_C\) は A に対する B の角速度 \(_A\boldsymbol{\omega}_B\) と B に対する C の角速度 \(_B\boldsymbol{\omega}_C\) の和から求めることができます. \begin{equation} _A\boldsymbol{\omega}_C = {_A}\boldsymbol{\omega}_B + {_B}\boldsymbol{\omega}_C. \label{eq13} \end{equation} この式の右辺は,ベクトルですので有限回転と異なり和の順は可換ですが,隣り合う添字が和を取ると消える形が分かり易いと思われます.また, \(_A\boldsymbol{\omega}_C=-_C\boldsymbol{\omega}_A\) ですので変形すると次式が成立します. \begin{equation} _A\boldsymbol{\omega}_B + {_B}\boldsymbol{\omega}_C + {_C}\boldsymbol{\omega}_A = 0. \label{eq14} \end{equation} これらの式は多数のプレートについても成立します.
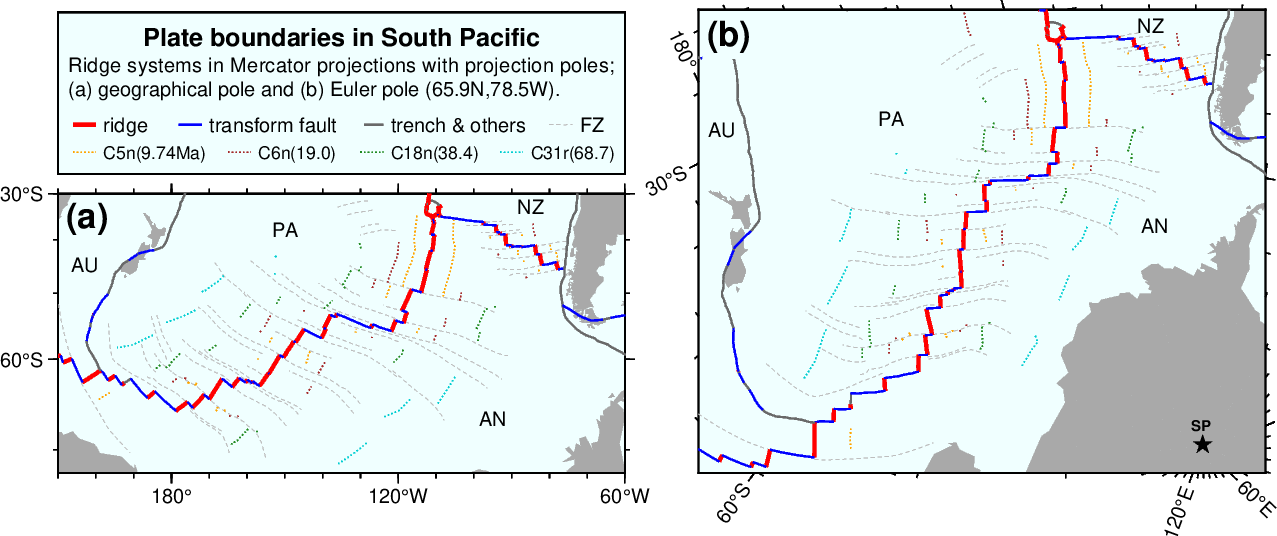
オイラー極によるメルカトール図法: プレート間の相対運動がオイラー回転で表せるならば,オイラー極を投影の極としたメルカトール図法ではトランスフォーム断層は水平に表わされるはずです.また,速度ベクトルが海嶺に垂直ならば,海嶺は垂直になるはずです. Le Pichon (1968) はこれを数例のプレート境界について示しました.このうちの1つである南太平洋について, DeMets et al. (2010) による最近のデータで下図に再現しました.
図 (a) は通常のメルカトール図法で,図 (b) では太平洋プレート(PA)に対する南極プレート(AN)の回転のオイラー極 (65.9°N, 78.5°W) が投影の極です.確かに,図 (b) ではトランスフォーム断層と海嶺が,ほぼ水平と垂直に見えます.しかし,図の下方にはかなり斜めのトランスフォーム断層もあり,完全には理論通りではないようです.また,回転の角速度 0.887°/My は 0.78 Ma (78万年前)の等年代線に基づいているので(遅いプレートは 3.16 Ma),図全体への適用はできません.オイラー極は時々別な地点に移動することが知られています.実際,緑色の点線で示した 38.4 Ma の等年代線付近で断裂帯は折れ曲がっています.これは,この頃にオイラー極が大きく移動したことを示し, 42 Ma 頃の太平洋プレートの移動方向の変化(ホットスポット起源のハワイ諸島-天皇海山列の屈曲)の現れと考えられます.
結局,図 (b) は教科書に載っている Le Pichon (1968) の図(例えば,上田 1989, p.74)が 1960 年代に与えたような大きなインパクトはないようです.それは,当時の海底地形や地磁気縞状異常などのデータは現在ほど詳細ではなく,図法の投影極を変えた効果が大きく現れたためと思われます.世界のプレート相対運動の研究は長年に渡り続けられ, RM-1 や NUVEL-1A などの幾つものモデルがより改善されながら提出されてきました.ここで使用した DeMets et al. (2010) のモデル MORVEL は GPS も含む新しい観測結果から 25 のプレートについて解析し,さらに上述の式 (14) やプレートの剛性などの基本原理がどの程度成立しているかも検討しています.
以下の演習問題で扱うデータは,少し古いモデルですが DeMets et al. (1990, 1994) によるプレート数が 14 で長年の標準モデルであった NUVEL-1A に基づいています.
問題7-3-1
下の図(右)はオイラー極 E と観測点 S の位置関係を示し, N は北極です.角 \(D\) と \(\delta\) は観測点に対するオイラー極の方位角と角距離です.図(左)は球面三角形の余弦定理と正弦定理を示します(球面三角法の説明は → ここにあります).
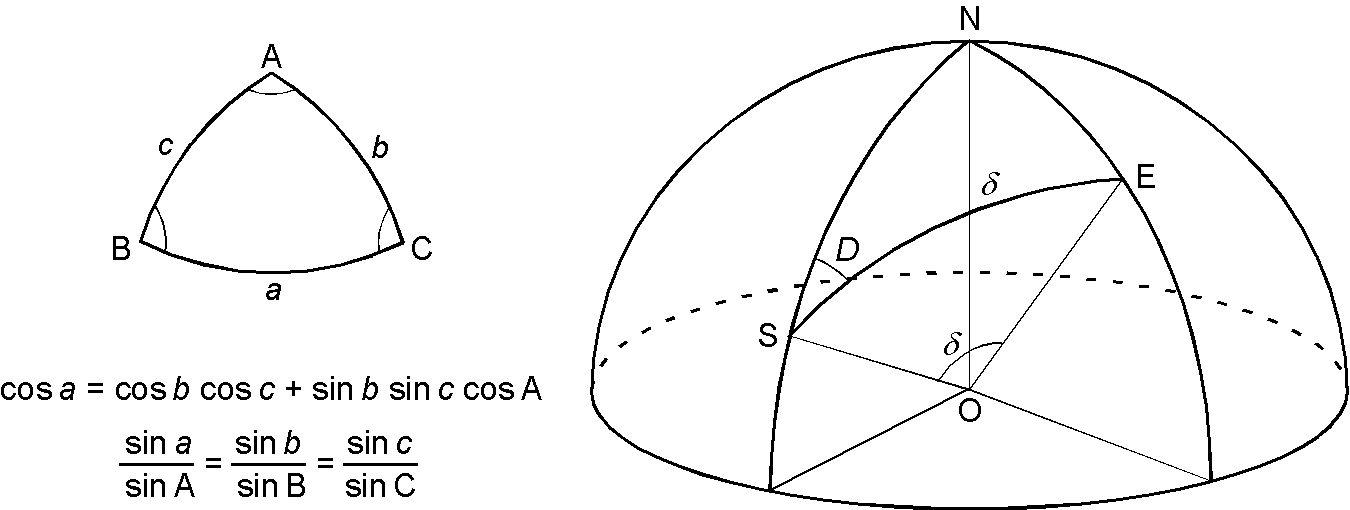
(1) オイラー極 E と観測点 S の (緯度,経度) を \((\lambda_E,\phi_E)\) と \((\lambda_S,\phi_S)\) とします.球面三角形の公式を適用して, \(\delta\) と \(D\) を求める次の式を導きなさい. \begin{eqnarray*} \cos\delta & = & \sin\lambda_E\sin\lambda_S + \cos\lambda_E\cos\lambda_S\cos(\phi_E-\phi_S), \\ \sin D & = & \frac{\cos\lambda_E\sin(\phi_E-\phi_S)}{\sin\delta}. \end{eqnarray*}
(2) 北米プレートに対するユーラシアプレートの回転運動は,オイラー極 (62.4°N, 135.8°E) と角速度 \(\omega\) = 0.21°/Myr で表わされます.では,アイスランド (65°N, 20°W) における,北米プレートに対するユーラシアプレートの相対速度の大きさ(cm/yr)と方向を求めなさい.地球半径を 6400 km とします.
(3) ユーラシアプレートに対する太平洋プレートの回転運動は, \(\boldsymbol{\omega}\) = (61.1°S, 94.2°E, 0.86°/Myr) で表わされます.では,東北沖 (38°N, 142°E) におけるユーラシアプレートに対する太平洋プレートの相対速度の大きさ(cm/yr)と方向を求めなさい.なお,この問いでは日本列島をユーラシアプレートの東端とします(現在主流の説は,東北日本をオホーツクプレートの一部や独立のマイクロプレートとするようです).
問題7-3-2
インド大陸が白亜紀以降北上しユーラシア大陸に衝突したことは古地磁気研究から分かります(→ 問題6-5-1を参照).現代もインドプレートが北上していることは地震の分布などから明らかです.しかし,ユーラシアプレートに対するインドプレートの回転運動の角速度は,両者の間に海嶺がないため測定できません.そこで,角速度が直接測定された他のプレート・ペアのデータから推定することにします.
ユーラシアプレート,北米プレート,アフリカプレート,インドプレートをそれぞれ EU, NA, AF, IN で表わします.次表で角速度ベクトルの添字は,例えば \(_{EU}\boldsymbol{\omega}_{NA}\) はユーラシアプレートに対する北米プレートの回転を示します. \((\lambda_E,\phi_E)\) はオイラー極の(緯度,経度)です. \(\omega\) の単位は地心直交座標 x-y-z での成分も含めて deg/Myr で,成分については計算中の桁落ち対策として小数点以下4桁表示としました.
| \(\boldsymbol{\omega}\) | \(\lambda_E\) (°N) | \(\phi_E\) (°E) | \(\omega\) (°/Myr) | \(\omega_x\) | \(\omega_y\) | \(\omega_z\) |
| \(_{EU}\boldsymbol{\omega}_{NA}\) | -63.2 | -45.5 | 0.22 | 0.0695 | -0.0707 | -0.1964 |
| \(_{NA}\boldsymbol{\omega}_{AF}\) | 73.7 | 94.8 | 0.21 | -0.0049 | 0.0587 | 0.2016 |
| \(_{AF}\boldsymbol{\omega}_{IN}\) | 25.5 | 26.8 | 0.39 |
(1) \(_{AF}\boldsymbol{\omega}_{IN}\) の地心直交座標系の各成分を本文の式 (12) を用いて計算しなさい.
(2) 本文の式 (13) を4つのプレートに拡大した式, \[ _{EU}\boldsymbol{\omega}_{IN} = {_{EU}}\boldsymbol{\omega}_{NA} + {_{NA}}\boldsymbol{\omega}_{AF} + {_{AF}}\boldsymbol{\omega}_{IN} \] を用いて \(_{EU}\boldsymbol{\omega}_{IN}\) の各成分を計算し,オイラー極の緯度・経度と角速度の大きさを求めなさい.
(3) インドの地点 S (\(\lambda_S\) = 20°N, \(\phi_S\) = 80°E) における,ユーラシアプレートに対するインドプレートの速度ベクトル \({\bf v}\) を,次の本文の式 (10) を用いて計算しなさい. \[ \left(\begin{array}{c} v_x \\ v_y \\ v_z \end{array}\right) = \left(\begin{array}{c} \omega_x \\ \omega_y \\ \omega_z \end{array}\right) \times\left(\begin{array}{c} r_x \\ r_y \\ r_z \end{array}\right) = \left(\begin{array}{c} \omega_yr_z - \omega_zr_y \\ \omega_zr_x - \omega_xr_z \\ \omega_xr_y - \omega_yr_x \end{array}\right). \] ここに, \({\bf r}\) は地点 S の距離ベクトルで,地球半径を \(a\) = 6400 km として次式となります. \[ \left(\begin{array}{c} r_x \\ r_y \\ r_z \end{array}\right) = \left(\begin{array}{c} a\cos\lambda_S\cos\phi_S \\ a\cos\lambda_S\sin\phi_S \\ a\sin\lambda_S \end{array}\right). \]
(4) 問い (3) で得た地心直交座標での速度ベクトル \({\bf v}\) を地点 S における局地座標 n-e-d (北-東-鉛直下)での表現 \({\bf v}_L\) に変換し,速度ベクトルの方向を求めなさい.変換式は次の通りです(導き方は → ここにあります). \[ \left(\begin{array}{c} v_n \\ v_e \\ v_d \end{array}\right) = \left(\begin{array}{ccc} -\sin\lambda_S\cos\phi_S & -\sin\lambda_S\sin\phi_S & \cos\lambda_S \\ -\sin\phi_S & \cos\phi_S & 0 \\ -\cos\lambda_S\cos\phi_S & -\cos\lambda_S\sin\phi_S & -\sin\lambda_S \end{array}\right) \left(\begin{array}{c} v_x \\ v_y \\ v_z \end{array}\right). \]
参考文献:
- DeMets, C., R.G. Gordon, D.F. Argus, and S. Stein, Current plate motions, Geophys. J. Int., 101, 425-478, 1990.
- DeMets, C., R.G. Gordon, D.F. Argus, and S. Stein, Effect of recent revisions to the geomagnetic reversal timescale on estimates of current plate motions, Geophys. Res. Lett., 21, 2191-2194, 1994.
- DeMets, C., R.G. Gordon, and D.F. Argus, Geologically current plate motions, Geophys. J. Int., 181, 1-80, 2010.
- Le Pichon, X., Sea-floor spreading and continental drift, J. Geophys. Res., 73, 3661-3697, 1968.
- 瀬野徹三, プレートテクトニクスの基礎, 200 pp., 朝倉書店, 東京, 1995.
- 上田誠也, プレート・テクトニクス, 268 pp., 岩波書店, 東京, 1989.