3-1 地球の形と大きさ
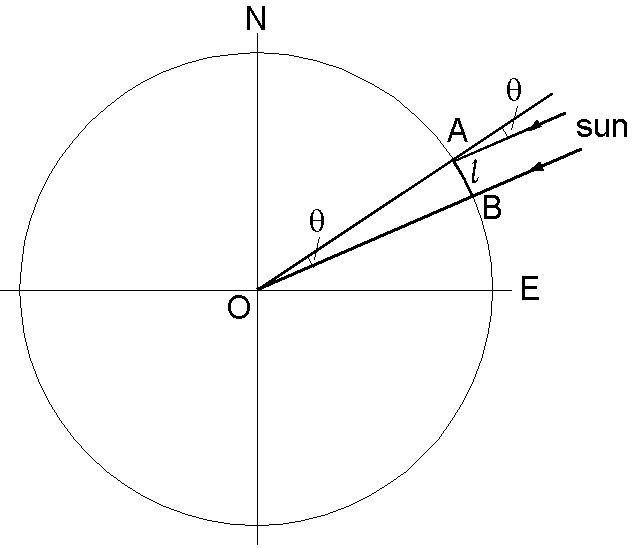
地球が球であることは人工衛星からの画像で容易に確認できますが,これを普通の生活で実感することは難しいです.例えば,異なる緯度での星空の見え方や太陽の動きの違いなどを観察して初めて地球が丸いことを推測できます.しかし,2千年以上も前にギリシャのエラトステネスは,地球の全周を測定しています.夏至の日にシェネの町(現アスワン)の深井戸に太陽が真上から照らすのに対して,北方のアレクサンドリアでは太陽が天頂から 7.2° 傾いていることから計算しました.右図で, A (アレクサンドリア)と B (シェネ)の距離を \(\ell\) とし, A での傾き角を \(\theta\) とすれば,地球の全周 \(L\) は次式で求まります. \[ L = \ell\times\frac{360}{\theta}, \] エラトステネスはおよそ 46000 km の値を得たといわれており,現代の測地学による子午線全周の値 40008 km より 15% 大きいだけです.
実際の地球は赤道の回りに膨らんだ楕円体に近い形をしています.このことは18世紀に,経度線に沿った緯度1度に相当する距離の測定が行われ,緯度が高いほど長いことから判明しました.地球の形は楕円を短軸のまわりに回転させた回転楕円体に近く,実際の地球に最も近いものを地球楕円体といいます.回転楕円体の扁平率 \(f\) は,赤道半径 \(a\) と極半径 \(b\) を用いて, \[ f = \frac{a - b}{a}, \] で定義され,地球楕円体では約 1/298 です (\(a\)=6378.137 km, \(b\)=6356.752 km).これは,赤道の直径が 30 cm の地球儀を考えると,自転軸方向の直径が 1 mm 短いだけとなり,ほとんど球に近いことが分かります.しかし,測地学では地球楕円体は地球表面の複雑な起伏を正確に記述するための基準として極めて重要です.なお,重力ポテンシャルによる扁平率を → 問題3-5-1 で考察します.
地球の形が回転楕円体に近いという事実は偶然ではないと考えられています.地球楕円体は仮に液体の地球が自転しているとした場合の形とほぼ等しいことが知られています.これは地球が自転による遠心力で膨らんだことを示唆し,地質学的時間スケールでは固体の地球も流体として振舞うためと考えられています.
問題3-1-1
地球を球として,ある高さから見渡すことのできる範囲を考えます.地球の半径を \(a\),目の高さを \(h\) として,その範囲の地球表面に沿って測った距離 \(\ell\) は次の近似式で表されることを示しなさい. \[ \ell = a\sqrt{\frac{2h}{a+h}}. \] 但し,次の小さい \(x\) についての \(\cos x\) の近似式を使用します. \[ \cos x \approx 1 - {\scriptsize \frac{1}{2}}x^2. \quad (|x| \ll 1) \] また,地球半径を 6400 km とすると,目の高さが 1 m,10 m,100 m の場合について \(\ell\) はそれぞれ何 km になるか?
問題3-1-2
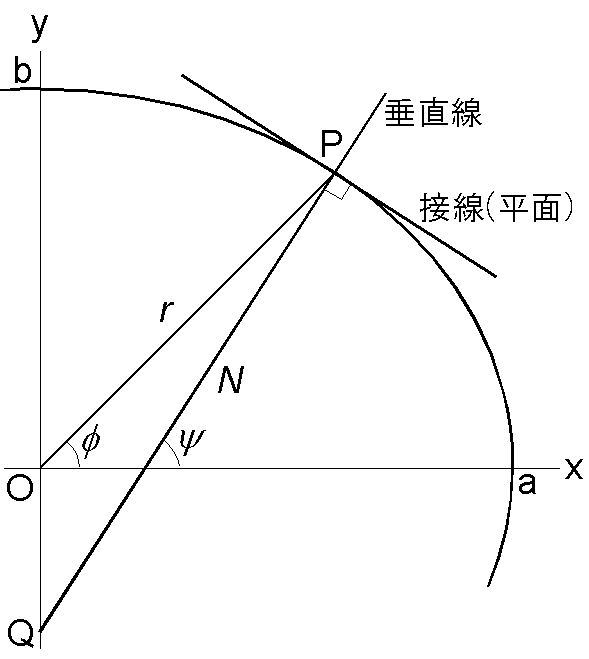
地球楕円体上で点 P の緯度を表す角度には2通りあります.右図で,点 P と地球中心を結ぶ線が赤道面となす角度 \(\phi\) を地心緯度,点 P での垂直線が赤道面となす角度 \(\psi\) を測地緯度(地理緯度)といいます.地図やナビゲーションなどで一般に使用されている緯度は後者の測地緯度です.
また,楕円の形状を表すパラメーターとして,上記の扁平率 \(f\) の他に,惑星の公転軌道などに広く使用される離心率 \(e\) があり,次式で定義されます. \[ e = \frac{\sqrt{a^2-b^2}}{a} \quad (a \geq b). \] 楕円では 0 < \(e\) < 1 で, \(e\) = 0 は真円を表します.
- (1) 点 P と地球中心との距離 \(r\) は,地心緯度 \(\phi\) を用いて次式で表されることを導きなさい. \[ r = \frac{b}{\sqrt{1-e^2\cos^2\phi}}. \]
- (2) 地心緯度 \(\phi\) と測地緯度 \(\psi\) との間の次の関係式を導きなさい. \[ \tan\phi = \frac{b^2}{a^2}\tan\psi. \]
- (3) 図のように,点 P での垂直線と自転軸との交点を Q とするとき, PQ の距離 \(N\) は測地緯度 \(\psi\) を用いて次式で表されることを導きなさい. \[ N = \frac{a}{\sqrt{1-e^2\sin^2\psi}}. \]