古地磁気学と岩石磁気学の基礎

an image of dinosaurその他：簡単な古地磁気計算機； pcalc

プログラム "pcalc" は双方向形式のユーティリティを提供し，単純な計算機として古地磁気データのマニュアル計算を可能にします．使用には， "pcalc" を "-A" オプションで起動します（"A" は "assorted" の略）．項目の一覧が表示されたら，使用したい項目の番号をタイプします．

フィッシャー統計の例

次のスナップショットは，"項目７番"による，８個の試料の磁化方向からのフィッシャー統計を示します．

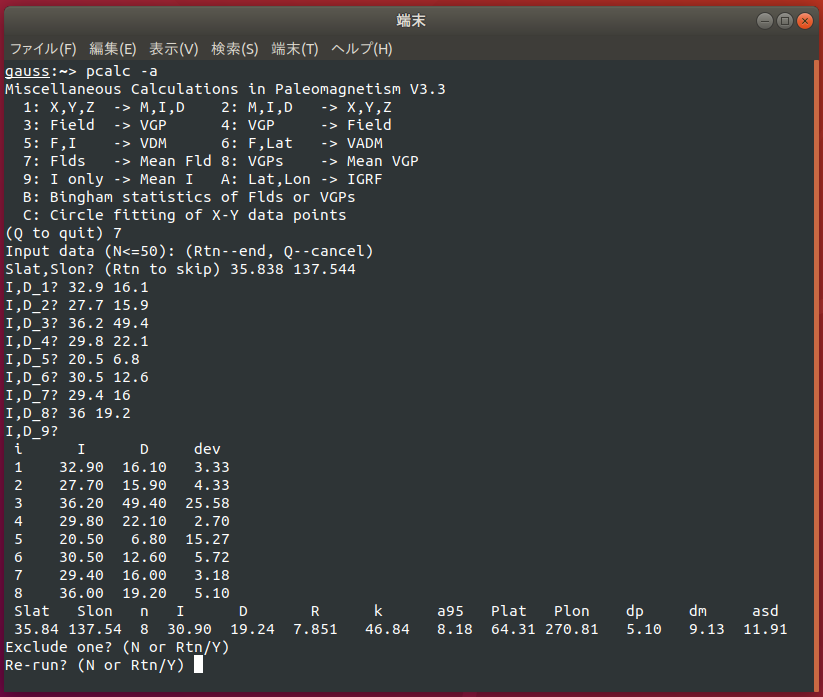
pcalc を使用したフィッシャー統計のマニュアル計算の例．

プログラムは統計結果からデータを１つ除外するかどうかを聞いてきます．しかし，この機能は都合の悪いデータを任意に消去することを推奨しているわけではありません． McFadden (1982) による outlier （外れ値）の統計検定を実施するべきで，プログラム "tmeandir" により可能です．

ビンガム統計の場合

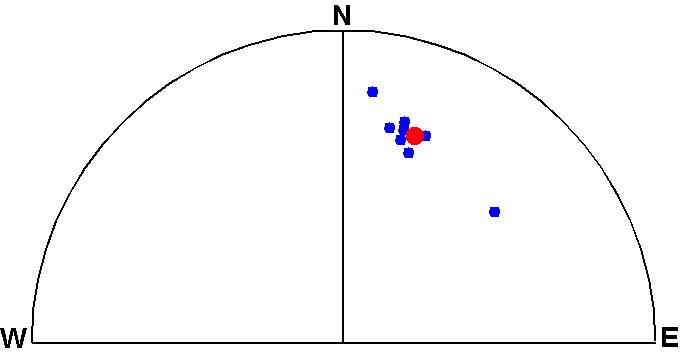
伸長した分布の８つの古地磁気方向．

上記の"項目７番"で入力したデータは図のようにかなり伸長した分布で，おそらく残留磁化の２次成分が十分に消去されていないと思われます． "項目 B" (Bingham statistics of Flds or VGPs) を選択し，同じデータを入力すると，次の統計結果が最後のフィッシャー統計とともに表示されます（最初に警告メッセージが表示されますが，"Return/Enter"キーを押して続行します）． 

Bingham statistics:
  n     k1     k2     tau1   tau2   tau3
  8  -214.49 -15.43   0.02   0.27   7.71
  I3(Lat3) D3(Lon3)  I2(Lat2) D2(Lon2)  I1(Lat1) D1(Lon1)
     30.83   18.95     21.51  122.56     50.93  241.61
  a31    a32    a21     Xu     Xcp     Xcg
  2.44   9.25  14.04   35.83   24.93   57.41
Fisher statistics:
  n Im(Latm) Dm(Lonm)   R       k     a95    Asd
  8   30.90   19.24    7.85   46.84   8.18  11.91

表示されたパラメーターのうち，固有ベクトル \({\bf t}_3\) の方向はタイトル "I3(Lat3) D3(Lon3)" の下に記されています．この方向は "項目７番" のフィッシャー統計で得られた平均方向（又は，タイトル "Im(Latm) Dm(Lonm)" の下に記された値）と大変良く一致しています．しかし，ビンガム統計は 95% 信頼域が大きく伸長していることを明らかにしました．それは， \(\alpha_{32}\) が \(\alpha_{31}\) よりもずっと大きいからです（タイトル "a31 a32" の下に記された値）．

IGRF による主磁場成分

"項目 A" は IGRF-13 を使用して n=m=10 までの和による主磁場成分の計算を提供します．期間は AD 1900~2025 です． 

geomagnetic elements of IGRF-13 up to n=m=10.
  ** Geodetic coordinate system WGS-84 (lat,lon) & altitude = 0 km. **
  ** Give the date in decimal year (ex.: 2020.3333 for 1 May 2020)  **
  ** For more options such as geocentric system, use program "igrf" **
Continue? (Rtn or Y/N) 
Decimal year? 2020.2
Year: 2020.20
Slat,Slon? -40.3 175.7
 Slat    Slon  F(nT)   I      D
-40.30  175.70 55180 -65.51  22.23
Slat,Slon?

標高を指定しての磁場成分や地心座標による観測点の値が必要な場合は，もう一つのプログラム "igrf" が利用できます．但し，計算は同じく n=m=10 までで行ってます．

円近似

"pcalc" のユニークな機能としては，２次元 X-Y データの Taubin 法による円近似です．これの元来の目的は古地磁気強度データ解析での使用ですが，次の例のように一般のデータにも応用できます． "項目C" を選び，４つのデータを入力した結果は次の通りです． 

Input X-Y data (3<=N<=50)
X,Y_1? 1.1 0.0
X,Y_2? 0.0 0.9
X,Y_3? -1.1 0.0
X,Y_4? 0.0 -0.9
X,Y_5? 
 i     X         Y         Error
 1    1.100     0.000     0.09501 
 2    0.000     0.9000   -0.1050  
 3   -1.100     0.000     0.09501 
 4    0.000    -0.9000   -0.1050  
 N   X0        Y0        R         k         SSE
 4  0.000     0.000     1.005     0.000     0.04010 
Exclude one? (N or Rtn/Y)

"(X0,Y0)" と "R" はそれぞれ近似した円の中心と半径です．注意すべき点として，半径 R が本来の値 1 より僅かに大きいことです．この理由は，プログラムが最小にする量は "代数学的" 距離 "\(r_i^2 - R^2\)" の二乗の合計であって， "幾何学的" 距離 "\(r_i - R\)" のそれではないからです．ここに \(r_i\) はデータ点の中心からの距離です．代数学的近似は幾何学的近似よりも正確さは劣りますが，前者のアルゴリズムがより単純な為に広く使用されています．理論の詳細は Chernov & Lesort (2005) にあります． "k" と "SSE" はそれぞれ曲率を表すパラメータと， \(r_i-R\) で表される誤差の二乗の合計です．これらは古地磁気強度データの評価に使用されるパラメーターで，一般のデータには不要です（"pmagt401.tar.gz" に含まれる "MEMOS_pmagt401.pdf" を参考にしてください）．

↑ ページ冒頭

ファイルからのデータ入力

"pcalc" はまた "-A" 以外のオプションで，入力データをファイルから読み込むことができます．この場合には，データ数に制限はありませんが， outlier を除外するような双方向の機能はありません．そのため，これらのオプション使用時には計算結果を Unix のリダイレクションを使用してファイルに保存することができます（"-A" オプションでは使用しないでください）．次の例は，オプション "-I" で "t-inc.d" から読み込んだデータについての伏角のみの統計結果です．入力データのリストを表示するためにオプション "-L" も使用しています． 

pcalc -i -l t-inc.d > result.txt

出力ファイル "result.txt" の内容は次の通りです． 

Inclination only statistics of t-inc.d:
Arith. mean: Im= 68.78, km= 36.42
MLE estimations:
 n   Im      km     a95   iteration
 9  71.85   32.45   9.17      43
Input data:
 i    I     dev
 1  66.10  -5.75
 2  68.70  -3.15
 3  70.10  -1.75
 4  82.10  10.25
 5  79.50   7.65
 6  73.00   1.15
 7  69.30  -2.55
 8  58.80 -13.05
 9  51.40 -20.45

このケースでは計算の収束は大変早く， 43 回で終了しました．しかし，データによっては収束が悪いこともあり，このような場合には警告のメッセージが表示されます．

プログラムのダウンロードとインストーレーション

→ このページにあります．

補足の説明

VGP から磁場方向を求める計算

VGP の位置 \((\lambda_P,\phi_P)\) が与えられたとして，観測点 \((\lambda_S,\phi_S)\) における磁場方向 \((I,D)\) は，球面三角形の公式を用いて求めることができ，磁場から VGP を求める場合の逆となります．しかし， "pcalc" は地心双極子と次数１のガウス係数の関係を使用しています．ガウス係数を求める際は， VGP は実際には S 極であることを考慮して，次のように反対称の極位置 \((-\lambda_P,\phi_P-180)\) を使用します． \begin{eqnarray*} g_1^0 & = & \frac{\mu_0 M}{4\pi a^3}\sin(-\lambda_P) = -\frac{\mu_0 M}{4\pi a^3}\sin\lambda_P, \\ g_1^1 & = & \frac{\mu_0 M}{4\pi a^3}\cos(-\lambda_P)\cos(\phi_P-\pi) = -\frac{\mu_0 M}{4\pi a^3}\cos\lambda_P\cos\phi_P, \\ h_1^1 & = & \frac{\mu_0 M}{4\pi a^3}\cos(-\lambda_P)\sin(\phi_P-\pi) = -\frac{\mu_0 M}{4\pi a^3}\cos\lambda_P\sin\phi_P, \end{eqnarray*} ここに \(\mu_0\)， \(M\)， \(a\) はそれぞれ真空の透磁率，双極子モーメント，地球の半径です．次数１の地磁気ポテンシャルを使用して，磁場の３成分 \(X\)， \(Y\)， \(Z\) （それぞれ NS， EW， 鉛直成分） は次式で与えられます． \begin{eqnarray*} X & = & -g_1^0\sin\theta_S + (g_1^1\cos\phi_S + h_1^1\sin\phi_S)\cos\theta_S, \\ Y & = & g_1^1\sin\phi_S - h_1^1\cos\phi_S, \\ Z & = & -2 g_1^0\cos\theta_S - 2(g_1^1\cos\phi_S + h_1^1\sin\phi_S)\sin\theta_S, \end{eqnarray*} ここに， \(\theta_S=90-\lambda_S\) です．

フィッシャー統計

→ このページにあります．

ビンガム統計

→ このページにあります．

↑ ページ冒頭

伏角のみの統計

真の方向 P0 の回りにフィッシャー分布する方向 P を極座標で表した図．

伏角のみの統計が古地磁気学に導入されたのは 1960 年代で，それは偏角の測定を欠くことが多いボーリングコアの古地磁気データを解析するためです．コンピュータのアルゴリズムとして使用可能な最初の研究は Kono (1980) により提出されました．続いて発表された幾つかの研究のうち， McFadden & Reid (1982) による方法が古地磁気分野で最も多く使用されました．しかし， "pcalc" は Arason & Levi (2010) による最近の方法を採用しました．以下は伏角のみの統計の簡潔な解説です．

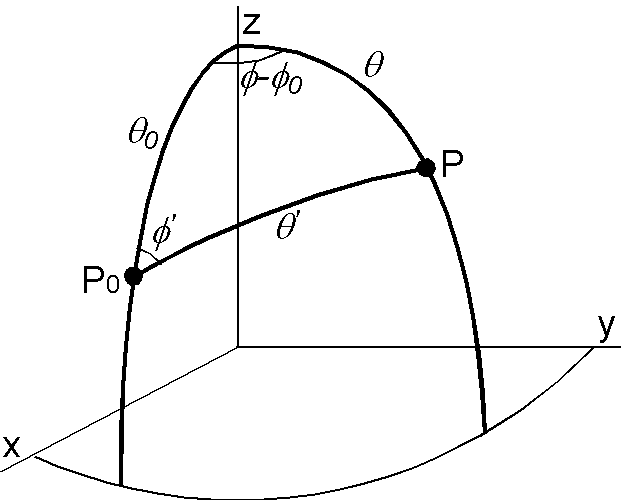
極座標を使用して，真の方向 P\(_0\)(\(\theta_0\),\(\phi_0\)) の回りにフィッシャー分布する方向 P(\(\theta\),\(\phi\)) を考えます． \(\theta^\prime\) と \(\phi^\prime\) をそれぞれ， P の P\(_0\) からの極角と P\(_0\) の回りの方位角とします． P の P\(_0\) の回りの確率密度関数は次式で与えられます． \[ f(\theta^\prime,\phi^\prime)d\theta^\prime d\phi^\prime = {\scriptsize \frac{\kappa}{4\pi\sinh\kappa} }\exp(\kappa\cos\theta^\prime)\sin\theta^\prime d\theta^\prime d\phi^\prime. \] 球面三角法を用いて（公式は → ここにあります），確率密度は次のように \((\theta,\phi)\) で表現されます． \[ f(\theta,\phi)d\theta d\phi = {\scriptsize \frac{\kappa}{4\pi\sinh\kappa} }\exp[\kappa\cos\theta_0\cos\theta + \kappa\sin\theta_0\sin\theta\cos(\phi-\phi_0)]\sin\theta d\theta d\phi. \] この式を \(\phi\) で積分すると， \(\theta\) の周辺分布（\(\phi\) の情報がない場合の \(\theta\) の確率密度）は次のようになります． \[ f(\theta)d\theta = {\scriptsize \frac{\kappa}{2\sinh\kappa} }\exp(\kappa\cos\theta_0\cos\theta)I_0(\kappa\sin\theta_0\sin\theta)\sin\theta d\theta, \] ここに， \(I_0(\cdot)\) は次数０の第１種変形ベッセル関数です． \(N\) 個の余緯度 \(\theta_i\) (\(i=1\cdots N\)) が与えられたとき， \(\theta_0\) と \(\kappa\) の最尤推定値は次の尤度関数を最大にすることで得られます． \begin{eqnarray*} h(\theta,\kappa) & = & \log\prod_{i=1}^N f(\theta_i), \\ & = & N\log\left({\scriptsize \frac{\kappa}{2\sinh\kappa} }\right) + \sum_{i=1}^N\log(\sin\theta_i) + \sum_{i=1}^N\kappa\cos\theta_0\cos\theta_i \\ & & + \sum_{i=1}^N\log(I_0(\kappa\sin\theta_0\sin\theta_i)). \end{eqnarray*}

これまでに出版された研究の主な違いは，上の尤度関数，特に変形ベッセル関数の近似の方法によります．ここでは， Arason & Levi (2010) が最も信頼性が高いと仮定しました．それは，方法の詳細な記述があることと，以前の方法による結果との徹底した比較検討がなされているからです．

国際標準地球磁場（International Geomagnetic Reference Field）

→ このページにあります．

円近似

→ このページにあります．

参考文献：

↑ ページ冒頭   → 次ページ