７-２ プレートテクトニクスの幾何学：平面上のプレート

プレートテクトニクスの概念は，地球表面は水平運動する何枚かのプレートで覆われており，地形・地震・火山などの地学現象はプレート境界で発生する，ということになります．プレートテクトニクスは誰にでも分かり易い概念ですが，個々の地学現象の理解には各分野の深い知識が必要です．このページでは，その基礎となるプレートの幾何学を平面上のプレートに限ってまとめます．

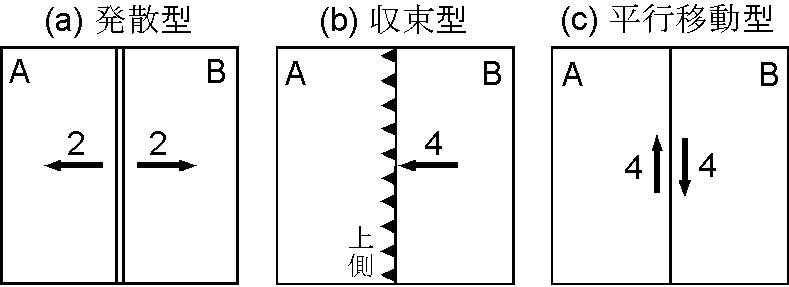
３種のプレート境界である，海嶺（a），海溝（b），トランスフォーム断層（c）の記号と速度表示の方法を右図に示します．（a）では片側拡大速度 2 cm/yr で海洋底が拡大する様子を，（b）ではプレート B が三角印が並んだ上盤のプレート A の下に向け相対速度 4 cm/yr で沈み込む様子を，（c）では２つのプレートが右横ずれ断層沿いに相対速度 4 cm/yr で移動する様子を示します．ここで，プレートの速度を表わす際に重要な概念は相対速度です．このページでは A に対する B の速度ベクトルを \(_A{\bf V}_B\) と表わします（添字を逆に表わす教科書もあります）．従って， \(_A{\bf V}_B = -_B{\bf V}_A\) の関係が常に成り立ちます．海嶺（a）の例では，片側拡大速度は 2 cm/yr ですが，相対速度ベクトルの大きさは，右向きを正とすると次のようになります． \[ _AV_B = -_BV_A = 4\ \mathrm{cm/yr}. \] 即ち，図（a）の発散型の場合だけ片側拡大速度を表示し，その他の場合には表示の速度は相対速度で，図（a）~（c）の全ての表示についてプレート A と プレート B の相対速度は 4 cm/yr です．

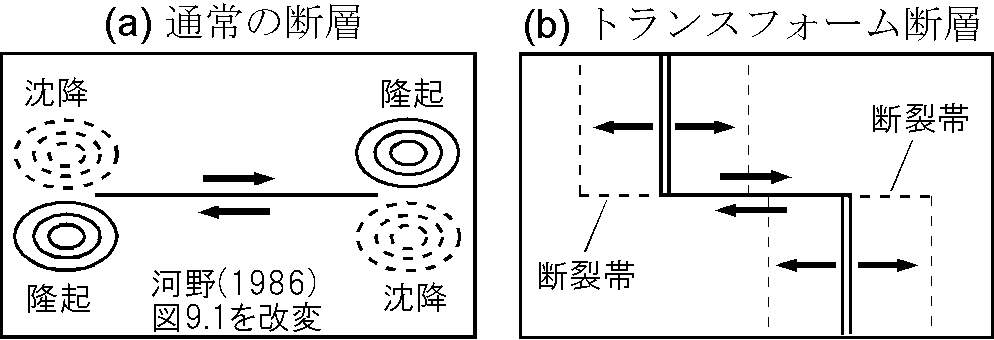
トランスフォーム断層： 海嶺は右図（b）のように所々で断層でずれていますが，断層の両端で特異な地形がないため発見当時は謎でした．それは，断層がずれ続けると両端で物質の過不足が生じ，（a）のような地形ができるからです．また，（b）で当初は一直線だった海嶺がずれたとすれば断層は左ずれですが，地震の発震機構（→ ４-３ 地震のメカニズム）からは右ずれでした．そこで，最初からずれて形成された海嶺から海洋底が両側に拡大していると考えれば解決します．この種の断層を Wilson (1965) がトランスフォーム断層と名付けましたが，それは断層が両端で海嶺や海溝に変容（transform）するという意味です．

また，上図（b）で海嶺で形成された海洋底が一定時間後に移動した位置を点線で示しましたが，これからこのトランスフォーム断層の長さは不変であることが分かります．なお，図で断層の延長線に示した太い破線は断裂帯（破砕帯）とよばれ，その両側で海洋底の年代が異なり，若い年代の海洋底ほど浅いために生じる断層のような地形です．

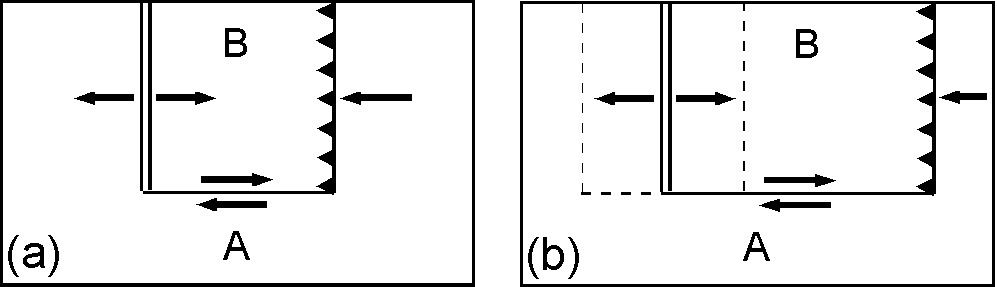
一方，時間とともに長さの増大するトランスフォーム断層もあり，右図にその例を示します．図の海溝ではプレート B が上盤で，プレート A が左に移動しながらプレート B の下に沈み込みます．一定時間経過後の（b）では，海洋底拡大で面積の増えたプレート B が上盤のため，海溝は右へ移動して断層の長さが増大することになります．

その他のトランスフォーム断層の例については，下の問題７-２-１で考察します．

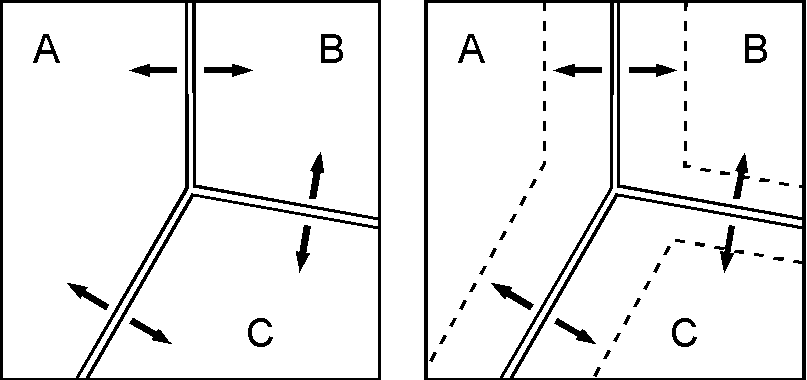
３重会合点： ３つのプレートが接する点を３重会合点（triple junction）といいます．右図は３つの海嶺（ridge）が交わる RRR 型の例で，ガラパゴス３重会合点（太平洋，ココス，ナスカの３プレート）やインド洋３重会合点（アフリカ，オーストラリア，南極の３プレート）が知られています． RRR 型では図（右）のように，時間が経過しても３重会合点の形は変わりません．但し，海洋底拡大の方向は海嶺に垂直で，速度は両側で等しいと仮定します（実際に多くの場合で成立します）．このように形の変わらない場合を安定な３重会合点といいますが，会合点が移動しても安定とします．それは，複数のプレートの位置関係はあくまで相対運動として表現されるからです．実際，上図では３重会合点はプレート A に対しては右から少し下向きの方向へ移動することになります．

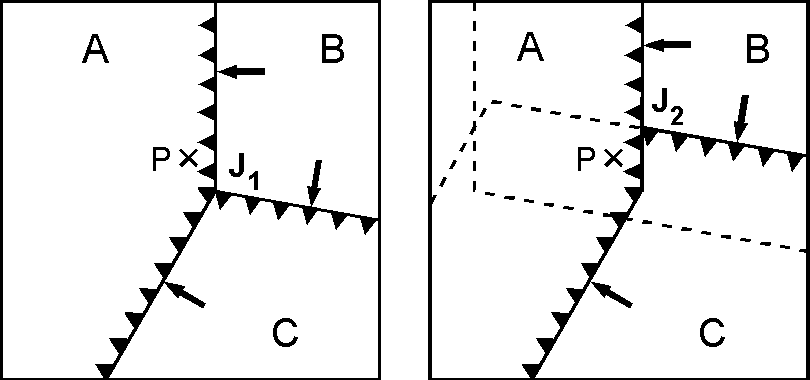
３つの海溝（trench）が交わる TTT 型の３重会合点とその時間変化を右図に示します（正確にはTTT(a)型）．この型は地球上で唯一の存在として房総沖に見られ，日本海溝，伊豆-小笠原海溝，相模トラフが交わっています（太平洋，北米，フィリッピン海の３プレート）．図（左）の３重会合点 J₁ は不安定で，時間の経過で図（右）のようになり，点線は沈み込んだプレートの端を示します．この図では各プレートは海溝に直角に沈み込むと仮定してますが，実際のプレートでは斜め沈み込みも多いです．一方，時間経過後の図（右）の J₂ もまた３重会合点です．しかし，ここでは３つの海溝のうち２つが一直線ですので安定となり， J₂ はプレート A に対して海溝に沿って上方に移動します．また， × 印で示した地点 P では当初はプレート B が海溝に直角に沈み込んでいたのが，時間経過後はプレート C が斜めに沈み込むことになります．このように，プレートが少し移動するだけで地学的に大きな変化が発生することもあります．

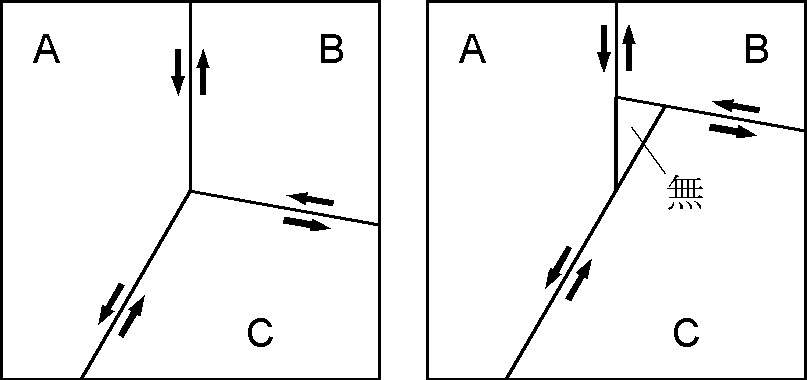
右図は３つのトランスフォーム断層が交わる３重会合点で，断層 fault の F から FFF 型といいます．この型の３重会合点は不安定で，地球上には存在しないようです．理論上は図のように時間の経過で何もない領域が発生してしまいます．

McKenzie & Morgan (1969) は 16 種類の３重会合点が存在するとし，その安定性を速度空間という概念を用いて議論しました．ここでは，そのうちの幾つかについて下の問題７-２-２と７-２-３で考察します．

↑ ページ冒頭

速度空間表示： プレート境界上で静止または移動する点の速度は，速度空間ではプレート境界の走行に応じた直線上の点となります．３重会合点は３つのプレート境界に同時に存在する点ですので，各プレート境界に対応する速度空間の３直線が１点で交われば３重会合点が存在することになります．また，交点の速度が３重会合点の移動速度となります．以下は Cox & Hart (1986) に基づいた説明です．

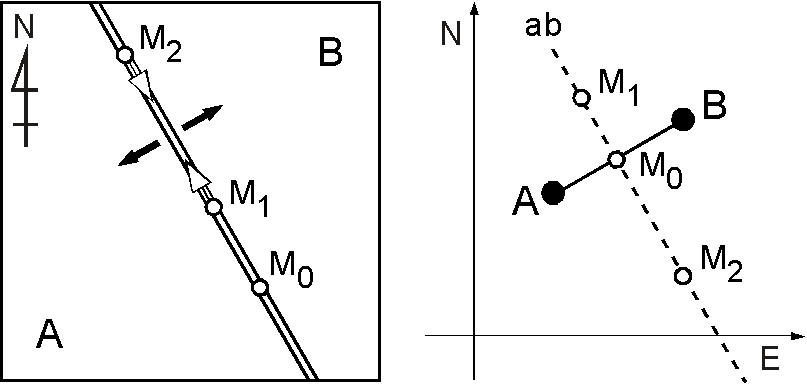
図（左）は海嶺の実空間表示で，プレート B はプレート A に対して東北東へ移動しています．また，白い丸印は海嶺上で静止（M₀）や移動（M₁とM₂）している点です．図（右）は速度空間表示で，横軸と縦軸はそれぞれプレートや海嶺上の点の移動速度の東西と南北の成分です．速度空間では海嶺の移動速度は A と B の中点となり， M₀ の速度も同様です． M₁ と M₂ の速度は，海嶺の実空間での走行と同じ直線，即ち線分 AB の垂直２等分線上となり，この直線を点線 ab で表わしています．

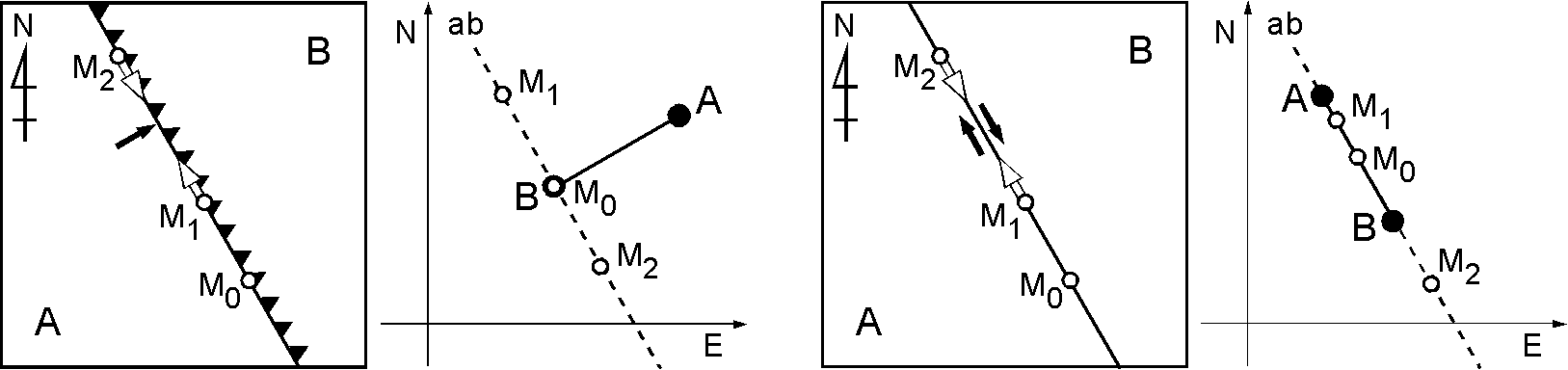
下図（左）の海溝ではプレート B が上盤ですので，海溝上で B の端で静止や移動する点について考えます．そのため速度空間では M₀ は B と一致します． M₁ や M₂ は海溝と同じ走行の点線 ab 上となります．図（右）のトランスフォーム断層も同様に考察して，速度空間では M₀~M₂ は線分 AB とその延長線の点線 ab 上となります．

速度空間作図例： 上の考察から，プレート A, B, C が交わるとき，速度空間で直線 ab, bc, ca を作図し，それらが１点で交われば３重会合点は安定となります．その例をこのページで最初に示した３重会合点について以下に示します．

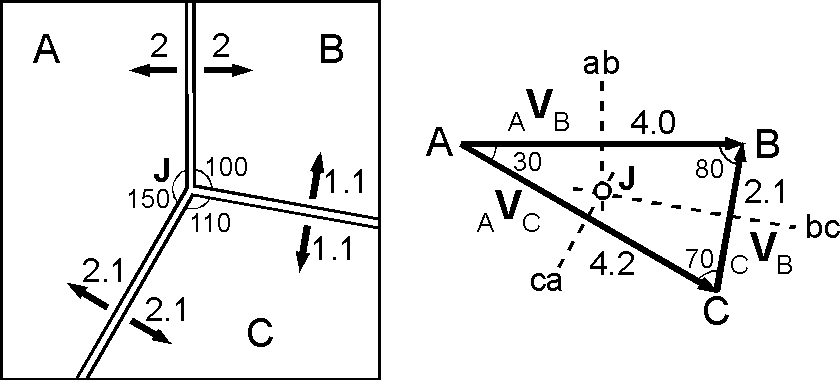
以下の図で上方を北とし，矢印の数字は cm/yr の拡大速度，小さい文字の数字は角度です．速度空間表示では，相対速度を問題とするので座標軸は省略します．右図の RRR 型３重会合点では，プレート A に対するプレート B の相対速度 \(_A{\bf V}_B\) は東向きで，その大きさをここでは 4 cm/yr とします．すると，海嶺の走行の角度からプレートの相対速度ベクトル間の角度が決まります．相対速度ベクトルについては， \[ _A{\bf V}_B + {_B}{\bf V}_C + {_C}{\bf V}_A = 0, \] ですので，図のような３ベクトルによる三角形が描けます．さらに正弦定理を用いて， \[ \frac{4}{\sin 70} = \frac{_AV_C}{\sin 80} = \frac{_CV_B}{\sin 30} = 2R, \] から \(_A{\bf V}_C\) と \(_C{\bf V}_B\) の大きさが求まります（R は外接円の半径）．三角形の各辺の垂直２等分線は１点 J で交わり３重会合点は安定です．さらに，三角形内の J の位置を計算することで，３重会合点 J はプレート A に対しては北から東回りに 110° の方角におよそ 2.1 cm/yr で移動することが分かります．なお，三角形の各辺の垂直２等分線は外心で１点で交わるので， RRR 型の３重会合点はこのような計算をするまでもなく常に安定です．

下図に TTT 型の３重会合点 J₁ と時間経過後の J₂ について，実空間と速度空間を示します．プレート A はプレート B と C に対して上盤ですので速度空間では直線 ab と ca は点 A を通り，プレート C は B に対して上盤ですので，直線 bc は点 C を通ります．３本の直線は１点で交わらず J₁ は不安定です．時間経過後の右図では，相対速度ベクトルの三角形は同じでも， ab と ca が一直線になったので，３本の直線は１点で交わり， J₂ は安定となります．速度空間での点 J₂ は点 A の真北方向で 1.46 離れているので，３重会合点 J₂ は海溝に沿って北向きに約 1.5 cm/yr で移動することが分かります．

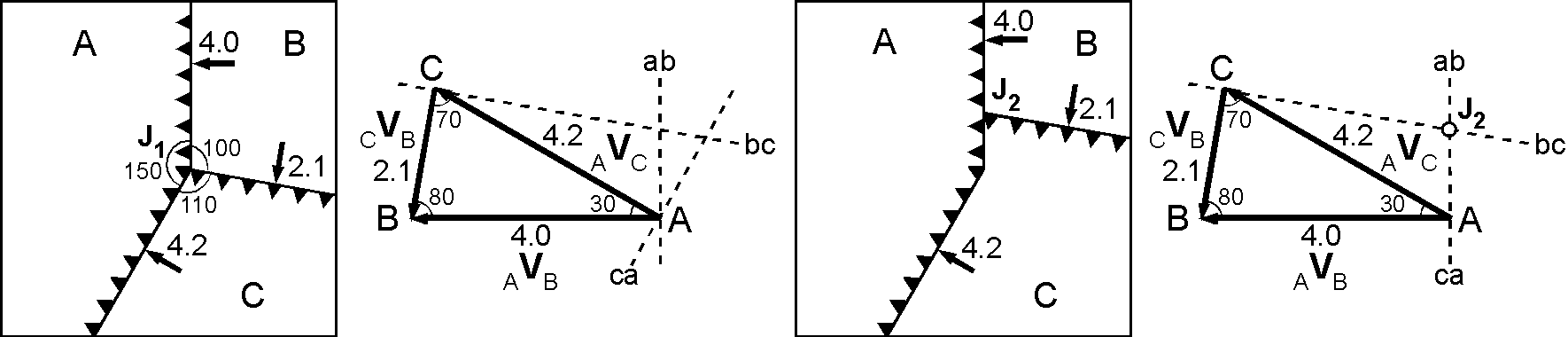
前述のように，房総沖の３重会合点は上図（左）の J₁ のような TTT 型です．不安定な３重会合点の存在理由については，現在が存在の一瞬であるとか，上図（右）の J₂ のようになっても地質構造の変化で（例えば陸側プレートが削られる） J₁ の形が保たれる等，専門レベルで議論があるようです．

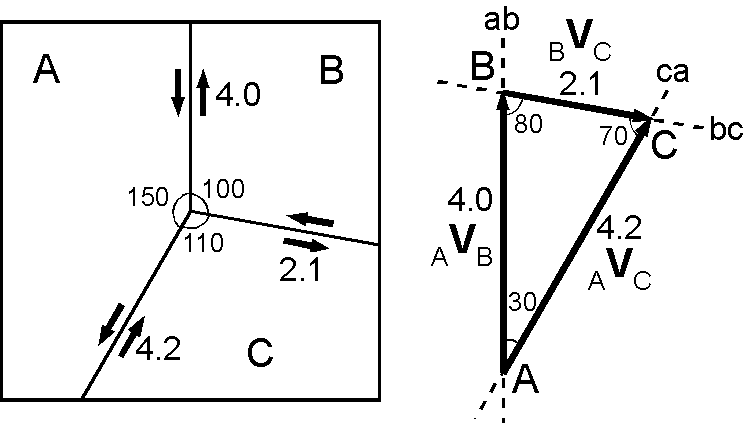
最後に FFF 型の３重会合点について，右図に実空間と速度空間を表示します．速度空間の３本の直線は相対速度ベクトルの三角形の辺と重なり，決して１点で交わることはなく， FFF 型はどんな場合にも不安定であることが分かります．

以上のような３重会合点の幾何学的考察が現実の地学現象の理解について役に立つのか疑問に思われるかも知れません．しかし，３重会合点の概念で初めて問題が解決された例は多く，その最大の成果は北米西海岸の長大なサンアンドレアス断層です．ここでは，その簡単なモデルについて下の問題７-２-３で考察します．

↑ ページ冒頭

問題７-２-１

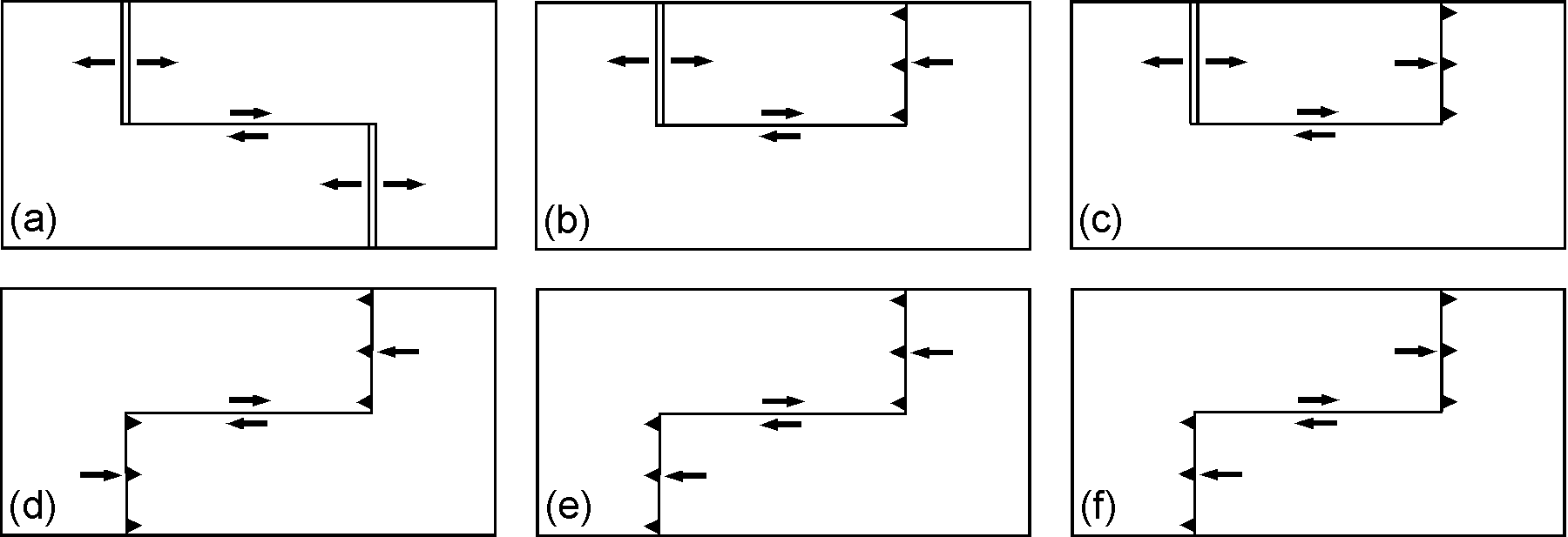
右横ずれのトランスフォーム断層には下図のように６種類あります（これらと鏡像対称の左ずれ断層も６種類あります）．それぞれの断層について，長さが不変，増大，減少のいずれになるかを調べなさい．

→ 解答

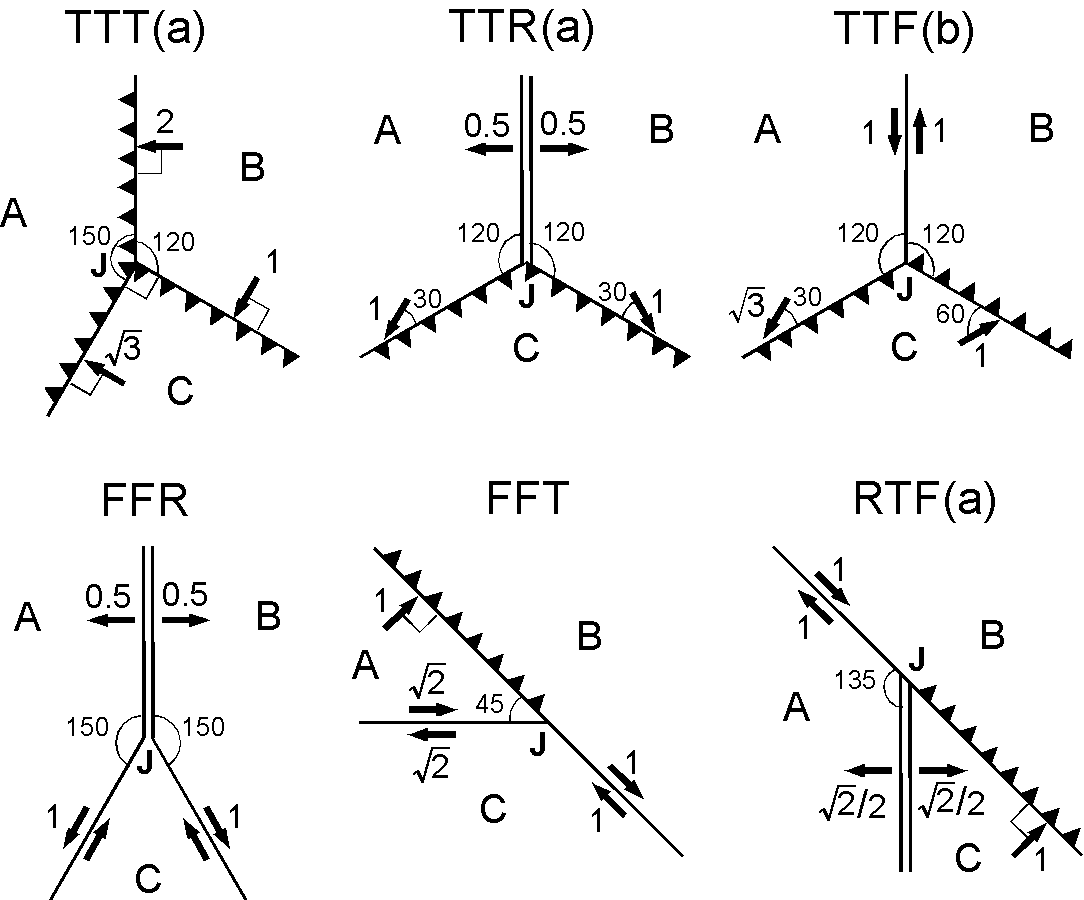
問題７-２-２

図は 16 の型がある３重会合点のうち任意に選んだ６個を示し，名称の一部の (a) などは同型に２種類ある場合を区別しています．図では上方が北で，矢印の数字は cm/yr 単位の相対速度（海嶺は片側拡大速度），小さい数字は角度を示します．３重会合点 J はいずれの場合も安定であることを速度空間表示を用いて示しなさい．また J の動きについて説明しなさい（例えば，「A に対して北へ移動」，「B に対して静止」，など）．

→ 解答

問題７-２-３

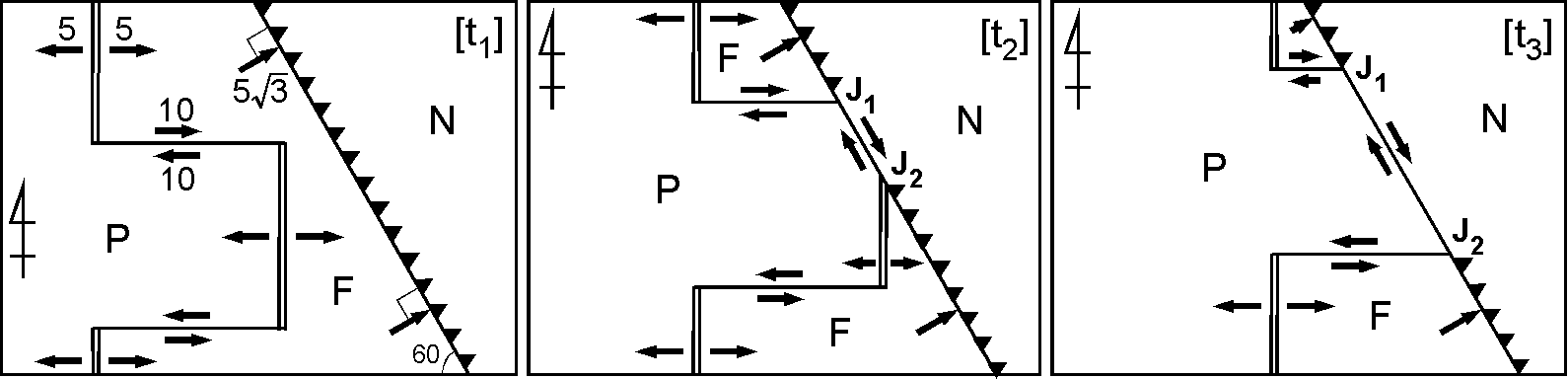
図は McKenzie & Morgan (1969) によるサンアンドレアス断層形成史のモデルです（cm/yr の速度や角度は改変しました）． P， N， F はそれぞれ太平洋プレート，北米プレート，ファラロンプレートです．時代 t₁~t₃ はおよそ 40~10 Ma で，海嶺が太平洋プレートに近づき，接触するとトランスフォーム断層が生じ，最後は消失した様子を示します．海嶺がトランスフォーム断層に変わる理由は，北米プレート（N）に対する太平洋プレート（P）の速度ベクトル \(_N{\bf V}_P\) が偶然に北米プレートとファラロンプレートの境界（北米の西海岸）に平行であったためです．なお，現在はファラロンプレートのほとんどは消失しましたが，その断片がファンデフカプレートとして残っていると考えられています．

では，３重会合点 J₁ と J₂ の北米プレート N に対する移動方向と移動速度を，時代 t₂ と t₃ のそれぞれについて求めなさい．

→ 解答

参考文献：

• Cox, A., and R.B. Hart, Plate Tectonics: How It Works, 392 pp., Blackwell Scientific Publications, Oxford, 1986.
• 河野長, 地球科学入門：プレート・テクトニクス, 195 pp., 岩波書店, 東京, 1986.
• McKenzie, D.P., and W.J. Morgan, Evolution of triple junctions, Nature, 224, 125-133, 1969.
• Wilson, J.T., A new class of faults and their bearing on continental drift, Nature, 207, 343-347, 1965.

↑ ページ冒頭   ← 前ページ   → 次ページ