ベクトルの回転:補足説明
2次元回転行列の導出(他の方法)
方法1:
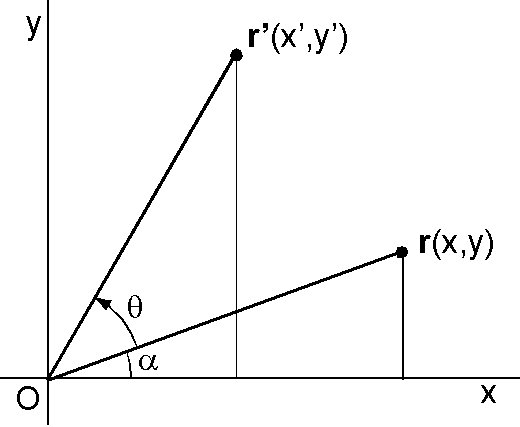
三角関数の加法定理による方法が最も簡単ですが,証明と言えるかは疑問です.それは,加法定理はこのような幾何学を用いて導かれているからです.しかし,三角関数の加法定理を覚えているときに便利です.図で,ベクトルの長さを1とすると, \begin{eqnarray*} x' & = & \cos(\theta+\alpha) = \cos\theta\cos\alpha - \sin\theta\sin\alpha, \\ & = & (\cos\theta)x - (\sin\theta)y, \\ y' & = & \sin(\theta+\alpha) = \sin\theta\cos\alpha + \cos\theta\sin\alpha, \\ & = & (\sin\theta)x + (\cos\theta)y. \end{eqnarray*} よって (x', y') は, \[ \left(\begin{array}{c} x' \\ y' \end{array}\right) = \left(\begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array}\right) \left(\begin{array}{c} x \\ y \end{array}\right), \] と表わされ,回転行列は \begin{equation} A = \left(\begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array}\right). \label{eq01} \end{equation}
方法2:
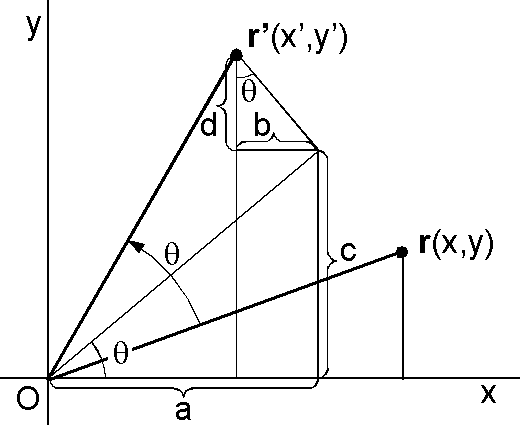
図には \({\bf r}\) の x 軸と y 軸への射影の長さ(x と y)を表わす線分を回転後の \({\bf r'}\) にも描いてあります(直角三角形が回転したように見える).回転角 \(\theta\) と同じ角度が2箇所ありますので,ベクトルの長さを1として, \begin{eqnarray*} x' & = & a - b, \\ & = & x\cos\theta - y\sin\theta, \\ y' & = & c + d, \\ & = & x\sin\theta + y\cos\theta. \end{eqnarray*} これより,式(1)と同じ回転行列となります. \[ A = \left(\begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array}\right). \]
方法3:
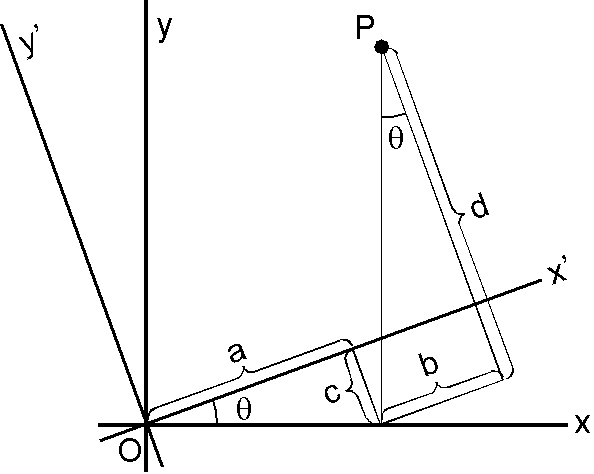
x-y 座標軸が \(\theta\) 回転して x'-y' 軸となった場合に,点 P の座標が (x, y) から (x', y') になるときの回転行列を求めます. \begin{eqnarray*} x' & = & a + b, \\ & = & x\cos\theta + y\sin\theta, \\ y' & = & -c + d, \\ & = & -x\sin\theta + y\cos\theta. \end{eqnarray*} よって (x', y') と (x, y) の関係は, \[ \left(\begin{array}{c} x' \\ y' \end{array}\right) = \left(\begin{array}{cc} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{array}\right) \left(\begin{array}{c} x \\ y \end{array}\right), \] となり,座標軸が回転するときの回転行列は \begin{equation} A = \left(\begin{array}{cc} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{array}\right). \label{eq02} \end{equation} この座標軸の回転行列(2)はベクトルの回転行列(1)とは異なることに注意する必要があります.但し,ベクトルの \(\theta\) 回転は座標軸の \(-\theta\) 回転と同等ですので,式(2)で \(\theta\) を \(-\theta\) で置き換えれば式(1)となります.