その他：サンコンパスによるオリエンテーション； sunpmag
古地磁気測定用の岩石試料は通常，携帯型エンジンドリルとサンコンパスによるオリエンテーション器具を用いて採取します．それはドリルとサンコンパスによる方法が最も正確で能率的だからです．このサンプリング方法は河野長博士（東工大および岡山大名誉教授）により日本に1960年代に導入されました．河野博士は太陽の方位角を計算するプログラムも導入しました．このプログラムは21世紀でも問題なく使用でき，誤差は ~0.1 度以下で古地磁気学の目的には十分に正確です．しかし， "sunpmag" は Yallop and Hohenkerk (2007) による最近の天文計算のアルゴリズムを導入しており，その誤差は 2000 BC から AD 2200 の間で ~0.6 分とのことです．"sunpmag" は夏原技研製作のオリエンテーター専用ですが，サブ関数の "sundir" は Yallop and Hohenkerk (2007) のアルゴリズムを正確に採用しており，一般的に太陽の方位角と高度を求めるのに役立つと思われます．
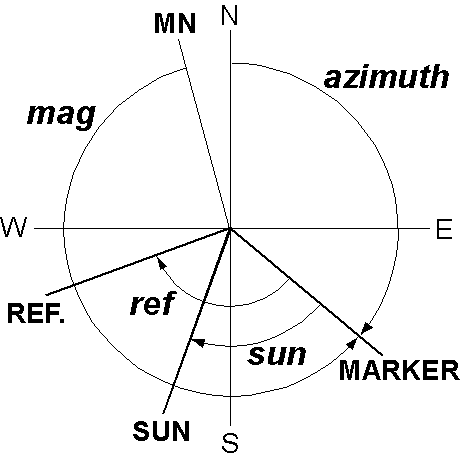右図は "sunpmag" で使用する測定のシステムです．ここで求めるべきは，コアのマーカーの真の北から時計回りに測定した方位角 azimuth です．しかし，フィールドで真の北を特定するのは困難ですので，１つないし３つの角度を測定します： mag, sun, ref です． mag はマーカーの角度で磁気的北から反時計回りに測定します． sun は太陽（太陽の影ではない！）の方向でマーカーから時計回りに測定します． ref はレファレンスの方向で，同様にマーカーから時計回りに測定します．試料採取地点における地磁気偏角が知れている場合はそれを測定データに含めますが，そうでない場合はプログラムは当該の日時と地点（標高 0 km）に対する IGRF または DGRF の値を計算します．
ある時刻における太陽の天球上での位置が分かれば，ある地点における太陽の方位角と高度は球面三角法を用いて求めることができます．その基本的な原理は以下の節で説明します．
プログラムのダウンロードとインストーレーション
球面三角法
以下に球面三角法の主な公式をまとめます．そのうちの幾つかは太陽の方位や高度を求めるのに使用されます．
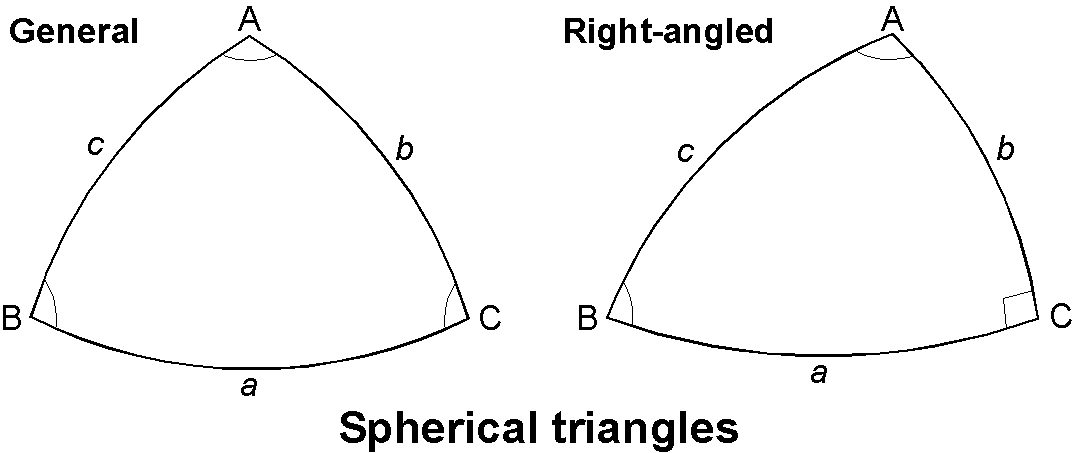
球面三角形は球面上の３本の大円によって囲まれた図形です．一般の球面三角形（左図）については， \begin{equation} \frac{\sin a}{\sin A} = \frac{\sin b}{\sin B} = \frac{\sin c}{\sin C}, \quad (\mathbf{正弦定理}) \label{eq01} \end{equation} \begin{equation} \cos a = \cos b \cos c + \sin b \sin c \cos A, \quad (\mathbf{余弦定理}) \label{eq02} \end{equation} \begin{equation} \cos A = -\cos B \cos C + \sin B \sin C \cos a, \quad (\mathbf{余弦定理}) \label{eq03} \end{equation} \begin{equation} \sin a \cos B = \cos b \sin c - \sin b \cos c \cos A, \quad (\mathbf{正弦余弦定理}) \label{eq04} \end{equation} \begin{equation} \cot a\sin b = \cos b\cos C + \sin C\cot A, \quad (\mathbf{余接定理}) \label{eq05} \end{equation} \begin{equation} \cot b\sin a = \cos a\cos C + \sin C\cot B, \quad (\mathbf{余接定理}) \label{eq06} \end{equation} 公式 (2)~(6) では，変数は順次並替え（輪環）が可能です．
\(\angle\)C = 90° の直角球面三角形（右図）については， (1) は次のようになります． \begin{equation} \frac{\sin a}{\sin A} = \frac{\sin b}{\sin B} = \sin c. \label{eq07} \end{equation} 公式 (4) において， \(a\)→\(b\), \(A\)→\(B\),\(\cdots\), などと記号を並替え， \(C\)=90° とすると，次の公式が得られます． \begin{equation} \tan a = \tan c \cos B. \label{eq08} \end{equation}
なお，球面三角形の内角の和は 180° より大きいです．このことは，球の半径を \(r\) として次式で表わされる三角形の面積 \(S\) が常に正であることから分かります． \begin{equation} S = (A+B+C-\pi)r^2. \label{eq09} \end{equation}
黄道座標から赤道座標への変換
太陽は天球上で黄道とよばれる大円の経路を１日当りおよそ１°移動します．太陽の天球上の位置を定める最初のステップとしては黄道座標が使用されます．黄道座標では，太陽の緯度（黄緯）は常にゼロで，それは太陽が黄道上に位置するからです．太陽の経度（黄経）は春分点から東向きに黄道に沿って測ります．天文学では黄経を表す記号として \(\lambda\) を使用しますが，ここでは \(\phi_E\) で表すことにします．それは，古地磁気学では前者は地理的緯度に使用されるからです．大雑把な近似としては，太陽の黄経 \(\phi_E\) は春分，夏至，秋分，冬至にはそれぞれ 0°， 90°， 180°， 270° となります．もちろん，ナビゲーションに十分な精度で太陽の黄経 \(\phi_E\) を見積もることは，このように単純ではありません．その理由は太陽の見かけの動きは一定ではないからです．これは地球の公転軌道が楕円で，自転も含めて種々の軌道要素が時間変動することに起因しています． Yallop and Hohenkerk (2007) のアルゴリズムはこれらの全てが考慮されています．但し，0.6分の精度に必要のない惑星の影響は除外されています．
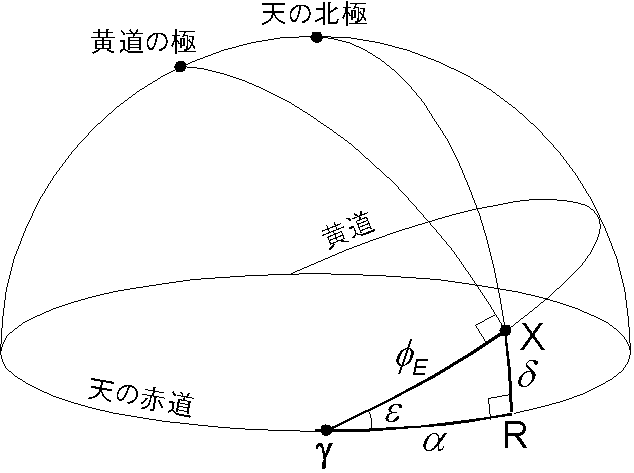
次のステップは太陽の位置を黄道座標から赤道座標へ変換することです．赤道座標では，緯度に相当する赤緯は天の赤道から北を正とし， \(\delta\) で表します．経度に相当する赤経は春分点から東向きを正とし， \(\alpha\) で表します．右図は春頃の太陽の位置を表し， X と \(\gamma\) はそれぞれ太陽と春分点です． R は天の北極と太陽を通る大円が天の赤道と交わる点です． \(\epsilon\) は黄道傾斜角で，およそ 23.5° です． \(\epsilon\) は時間的に変動しますが，プログラムは与えられた時間に対する値を計算します．
ある時刻に対する \(\phi_E\) と \(\epsilon\) が与えられれば， \(\alpha\) と \(\delta\) は直角球面三角形の公式を \({\scriptsize \triangle}\)X\(\gamma\)R に適用することで得られます．公式 (7) と (8) を使用して， \begin{eqnarray} \sin \delta & = & \sin \phi_E \sin \epsilon, \label{eq10} \\ \tan \alpha & = & \tan \phi_E \cos \epsilon. \label{eq11} \end{eqnarray} 式 (11) で得られた赤経 \(\alpha\) は，太陽が黄道のどの四分円に位置するかで値の調整が必要です．しかし， C 言語の関数 "atan2" を使用すればより簡単になります．
赤道座標から地平座標への変換
最後に，ある観測地点における太陽の方位角 \(A\) と高度 \(h\) を求めます．ここでは，天文学の慣習に従い，方位角 \(A\) は南から西向きを正とします．次の左図は北半球中緯度で夏の午後に観測される太陽 X を表しています．右図は同時刻における同経度の南半球中緯度の様子（冬の午後）を示します．
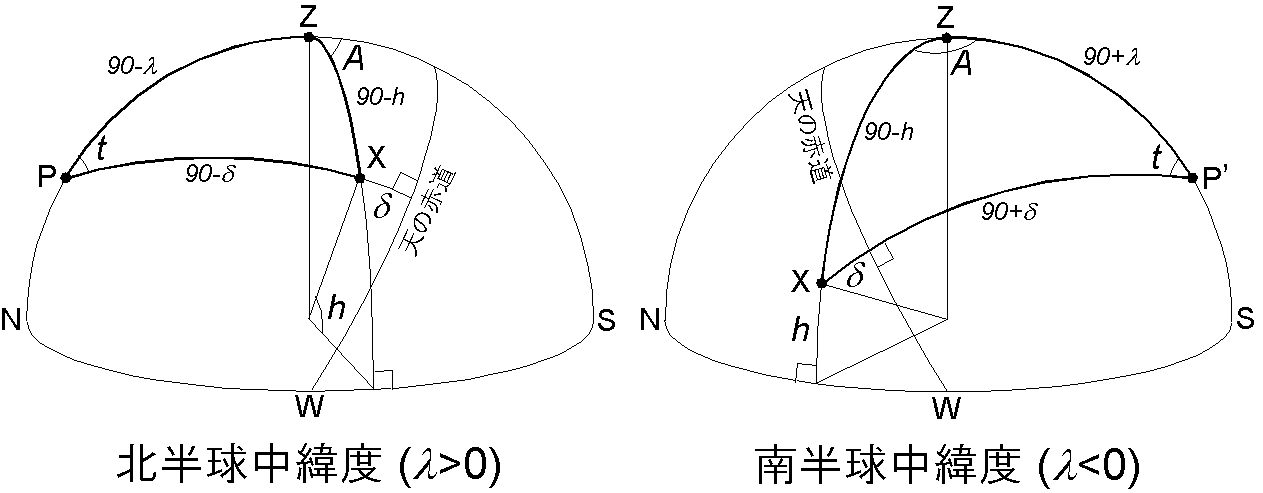
左図で P と Z はそれぞれ天の北極と天頂です．右図の P' は天の南極です． \(\lambda\) は観測地点の緯度で，左図（右図）では \(\lambda\)>0 （\(\lambda\)<0）です．太陽の赤緯 \(\delta\) は両図で同じ正の値です． \(t\) は観測地での太陽の時角で，子午線から西向きを正とします．天文学では通常 \(t\) を時間の単位で表しますが，ここでは角度の単位で表します．プログラムは指定された時刻におけるグリニッジでの太陽の時角 \(t_G\) をその時刻の赤経 \(\alpha\) やその他の軌道要素を用いて計算します．観測地での太陽の時角 \(t\) はグリニッジでの時角 \(t_G\) より観測地の経度 \(\phi\) だけ進んでいますので， \[ t = t_G + \phi. \] 左図で， \({\scriptsize \triangle}\)PXZ に式 (2) を適用することで次式が得られます． \begin{eqnarray} \cos(90-h) & = & \cos(90-\lambda)\cos(90-\delta) + \sin(90-\lambda)\sin(90-\delta)\cos t, \nonumber \\ \sin h & = & \sin\lambda\sin\delta + \cos\lambda\cos\delta\cos t. \label{eq12} \end{eqnarray} 方位角 \(A\) を求めるには，余接定理 (6) で記号を \(a\)→\(c\), \(b\)→\(a\), \(B\)→\(A\), \(C\)→\(B\) のように逆順に並替えた後に変形した次の式を用います． \[ \tan A = \frac{\sin B}{\sin c \cot a - \cos c \cos B}. \] この式を \({\scriptsize \triangle}\)ZPX に適用して， \begin{eqnarray} \tan(180-A) & = & \frac{\sin t}{\sin(90-\lambda)\cot(90-\delta) - \cos(90-\lambda)\cos t}, \nonumber \\ \tan A & = & \frac{\sin t}{\sin\lambda\cos t - \cos\lambda\tan \delta}. \label{eq13} \end{eqnarray} これらの太陽の方位角と高度を与える２つの式が右図や他の季節や時間についても成立することは容易に分かります．式 (13) による \(A\) の値は，球面三角形が鋭角三角形かどうかで調整が必要です．しかし，C 言語の "atan2" を使用すればより簡単になります．
参考文献：
- Yallop, B. D., and C. Y. Hohenkerk, Astronomical Algorithms for use with Micro-computers, NAO Technical Note No.67, HM Nautical Almanac Office, UK Hydrographic Office, 1989 (2007 updated). (→HM Nautical Almanac Office: Technical Notes)