２ 放射性元素と絶対年代

放射性崩壊と年代決定： 放射性元素(親元素)が崩壊して別な元素(子元素)が生成される放射性崩壊では熱エネルギーが発生し，固体地球の熱的現象として重要です．しかし，ここでは放射性元素が時間とともに減少することを利用して年代を決定する絶対年代決定の原理について学びます．

ある時刻における親元素の数を \(P\) とし，単位時間に崩壊する元素の割合(崩壊定数)を \(\lambda\) とすると， \(dt\) 時間内に崩壊する親元素の数 \(dP\) は，その時刻における親元素の数 \(P\) と時間 \(dt\) に比例するので， \[ dP = -\lambda P dt, \] で与えられます．これを微分方程式， \[ \frac{1}{P} dP = -\lambda dt, \] のように表し， \(C\) を積分定数として両辺を積分すると， \[ \log_e P = -\lambda t + C, \] となりますが，新たな定数， \(K = e^C\) ，を用いて変形すると， \[ P = K e^{-\lambda t}, \] となります．ここで， \(t=0\) における \(P\) を \(P_0\) とすると， \(P_0 = K\) ですので，一般に親元素の崩壊は次の指数関数で表されることになります． \begin{equation} P = P_0 e^{-\lambda t}. \label{eq01} \end{equation} また，親元素の数が最初の半分になる時間が半減期 \(T_{1/2}\) で， 次式で与えられます． \begin{equation} T_{1/2} = \frac{\log_e 2}{\lambda}. \label{eq02} \end{equation} 一方，子元素は親元素が減るのと全く同じ割合で増えることを利用して，時刻 \(t\) における子元素の数 \(D\) は， \(t = 0\) における子元素の数を \(D_0\) として，次式となることが分かります． \begin{equation} D = D_0 + P(e^{\lambda t} - 1). \label{eq03} \end{equation}

C-14 法： 自然に存在する炭素元素は ¹²C が 99%， ¹³C が 1% ですが，放射性元素の ¹⁴C が極微量だが一定の割合で CO₂ として存在します． ¹⁴C は宇宙線により生成された中性子 n が大気中の安定な窒素元素 ¹⁴N に衝突することで生成されます．生成された ¹⁴C は電子線のベータ線 β を放出して，半減期 5730 年で崩壊し元の ¹⁴N に戻ります．これらの反応は次式で表されます（p は陽子）．

大気中の ¹⁴C は放射性崩壊で減少する割合と宇宙線により生成される割合がバランスされ，常に一定であると仮定します．生物に含まれる ¹⁴C の存在比は呼吸活動により大気中と同じです．しかし，生物が死んだ時点で体内の ¹⁴C は外界との接触が断たれ，これを閉鎖系になったといいます．すると， ¹⁴C は時間の経過とともに減少するので，動植物の遺骸に含まれる ¹⁴C の量を測定すれば，死後の時間を求めることができます．即ち， C-14 法は親元素がどのくらい減っているかを測定することで年代を決定します．半減期が短いので，この方法は過去数万年程度の年代範囲に適用されます．但し， 1950 年以降の ¹⁴C 存在度が原水爆実験のために増加したので，AD 1950 年の値を初期値とします．年代は 3000 BP などと， AD 1950 から 3000 年前（Before Present）として表します．また，実際の測定では地磁気強度や太陽活動の変動の影響で ¹⁴C の存在度は変動するので，それらの効果の補正が必要となります．

↑ ページ冒頭

K-Ar 法： 自然に存在するカリウム元素は ³⁹K が 93%， ⁴¹K が 7% ですが，放射性元素の ⁴⁰K が約 0.01% 存在します． ⁴⁰K は半減期が約 12.5 億年で， 89% がベータ線 β を放出して ⁴⁰Ca へ， 11% が電子 e を捕獲して ⁴⁰Ar へと壊変します．

前者の ⁴⁰K → ⁴⁰Ca の系列は年代決定には使用されません．それは自然の ⁴⁰Ca が多量に存在するため，放射性崩壊により生じた分を正確に測定できないからです．後者の ⁴⁰K → ⁴⁰Ar の系列は，数万年前から数億年前の広い年代範囲で主に火成岩に適用されます．火成岩は固化した時点以降は外界と元素のやりとりがない閉鎖系ですので，一般に放射性年代決定は火成岩に適用されます．特にこの K-Ar 法では，火成岩形成時のマグマ中では，気体の ⁴⁰Ar の量はゼロですので式 (3) の \(D_0\) はゼロとなり，時刻 \(t\) における ⁴⁰Ar の量は式 (3) に係数 \(\lambda_\mathsf{e}/\lambda\) を掛けた次式となります（括弧は元素の量を表わします）． \[ (^{40}\mathsf{Ar}) = (\lambda_\mathsf{e}/\lambda)(^{40}\mathsf{K})(e^{\lambda t} - 1). \] ここに， \(\lambda_\mathsf{e}\) は ⁴⁰K → ⁴⁰Ar の壊変定数で， \(\lambda\) は ⁴⁰K 全体としての壊変定数です．結局， K-Ar 法は，現在における親元素と子元素の量を測定することで年代を決定します．

Rb-Sr法： その他の主な放射性年代決定法には U-Pb 法や Rb-Sr 法があり，ここでは後者を取り上げてアイソクロンという考え方を学びます． ⁸⁷Rb は 488 億年の半減期で放射性崩壊し， ⁸⁷Sr を生成します．半減期が長いので，一千万年前より古い年代に適用されます．時刻 \(t\) において式 (3) は， \[ (^{87}\mathsf{Sr}) = (^{87}\mathsf{Sr})_0 + (^{87}\mathsf{Rb})(e^{\lambda t} - 1), \] となりますが，通常は安定同位体 ⁸⁶Sr の量で割って次の形の式を利用します． \begin{equation} \left(\frac{^{87}\mathsf{Sr}}{^{86}\mathsf{Sr}}\right) = \left(\frac{^{87}\mathsf{Sr}}{^{86}\mathsf{Sr}}\right)_0 + \left(\frac{^{87}\mathsf{Rb}}{^{86}\mathsf{Sr}}\right)(e^{\lambda t} - 1). \end{equation}

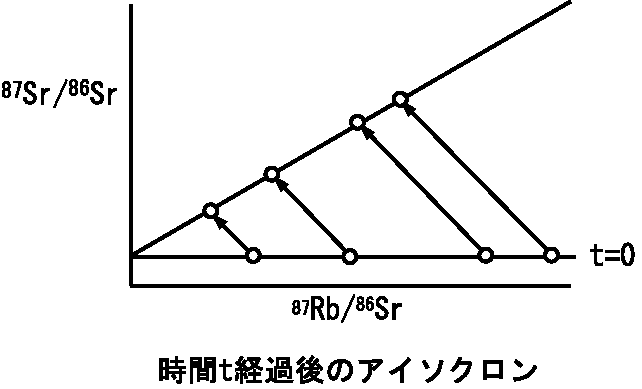
現在における， ⁸⁷Sr/⁸⁶Sr や ⁸⁷Rb/⁸⁶Sr の量を測定しても火山岩が生成された当時の (⁸⁷Sr/⁸⁶Sr)₀ がわからないと式 (4) は利用できません．しかし， (⁸⁷Sr/⁸⁶Sr)₀ が知られていなくても年代を決定できる方法があります．それは，同じ岩体の場所の異なる試料について測定し，横軸に ⁸⁷Rb/⁸⁶Sr を，縦軸に ⁸⁷Sr/⁸⁶Sr を取ってプロットすると，式 (4) が傾き \((e^{\lambda t}-1)\) の直線になることを利用します．この原理は，異なる元素の量比である ⁸⁷Rb/⁸⁶Sr は異なる岩体や鉱物では違った値を取り得るが，同じ元素である同位体の量比 ⁸⁷Sr/⁸⁶Sr は同じ値となることです．よって図のように，時刻 \(t=0\) では水平な直線が時間の経過とともに傾きが増大することになります．この直線を等時代線（アイソクロン）といいます．

↑ ページ冒頭

問題２-１

放射性元素による年代決定において， \(P_0\) と \(P\) をそれぞれ最初と現在の親元素の数， \(D_0\) と \(D\) をそれぞれ最初と現在の子元素の数，崩壊定数を \(\lambda\) とします．

• （１） 半減期が \(T_{1/2}=(\log_e 2)/\lambda\) となることを導きなさい．
• （２） \(P_0\) が分かっているとして， \(P\) の測定値から年代 \(T\) を求める式を導きなさい．
• （３） \(D_0\) が分かっているとして， \(P\) と \(D\) の測定値から年代 \(T\) を求める式を導きなさい．
• （４） ¹⁴C の含有量が初期値の 12.5% に減っている試料の年代を求めなさい．但し， ¹⁴C の半減期は 5730 年です．

→ 問題２-１ 解説

問題２-２

⁴⁰K の放射性崩壊は次の２系列あります．

時刻 \(t\) における各元素の量を \((^{40}\mathsf{K})\) などと表すとき，微小時間 \(dt\) において，親元素や子元素の増減は次式で表されます． \begin{eqnarray*} -d(^{40}\mathsf{K}) & = & d(^{40}\mathsf{Ca}) + d(^{40}\mathsf{Ar}), \\ d(^{40}\mathsf{Ca}) & = & \lambda_\beta(^{40}\mathsf{K})dt, \\ d(^{40}\mathsf{Ar}) & = & \lambda_\mathsf{e}(^{40}\mathsf{K})dt. \end{eqnarray*} これらの式を用い， \((^{40}\mathsf{Ar})\) の初期値がゼロであることを考慮して， \((^{40}\mathsf{K})\) と \((^{40}\mathsf{Ar})\) の測定値から年代 \(T\) を求める次式を導きなさい．但し， \(\lambda=\lambda_\beta + \lambda_\mathsf{e}\) とします． \[ T = \frac{1}{\lambda}\log_e\left(1 + \frac{\lambda}{\lambda_\mathsf{e}}\frac{(^{40}\mathsf{Ar})}{(^{40}\mathsf{K})}\right). \]

→ 問題２-２ 解説

問題２-３

SNC隕石と呼ばれる火星起源の隕石を Rb-Sr 法で測定した結果の一部を次表に示します．

データをプロットし，アイソクロンを描きなさい (→ グラフ用紙)．また， \(\lambda t\) は小さいので直線の傾きが次式で近似できることを利用して年代を求めなさい． \[ e^{\lambda t}-1 \approx \lambda t. \] 崩壊定数は， \(\lambda\) = 1.42\(\times\)10^-11 1/yr とします．

→ 問題２-３ 解説

問題２-４

放射性崩壊において，放射性元素の平均寿命は崩壊定数の逆数 \(1/\lambda\) となることを導きなさい．

→ 問題２-４ 解説

↑ ページ冒頭