1-1 ケプラーの法則
惑星の公転運動は一定の規則に従っており,地動説が唱えられて間もない17世紀初頭に次のケプラーの法則が発見されました.
- 第1法則:公転軌道は太陽を1つの焦点とする楕円である(楕円軌道の法則).
- 第2法則:太陽と惑星を結ぶ直線が一定時間に描く面積は一定である(面積速度一定の法則).
- 第3法則:公転周期の2乗は平均軌道半径の3乗に比例する(調和の法則).
次の表は第3法則を確認するために,惑星の公転周期 \(T\) と平均距離 \(a\) の単位をそれぞれ年と天文単位(au)として計算した結果です. \(T^2/a^3\) は有効数字3ケタ程度で一致していることが分かります.
| 惑星 | \(T\) | \(a\) | \(T^2\) | \(a^3\) | \(T^2/a^3\) |
| 水星 | 0.2409 | 0.3871 | 0.05803 | 0.05801 | 1.0005 |
| 金星 | 0.6152 | 0.7233 | 0.3785 | 0.3784 | 1.0002 |
| 地球 | 1 | 1 | 1 | 1 | 1 |
| 火星 | 1.8809 | 1.5237 | 3.5378 | 3.5375 | 1.0001 |
| 木星 | 11.862 | 5.2026 | 140.71 | 140.82 | 0.9992 |
| 土星 | 29.457 | 9.5549 | 867.71 | 872.33 | 0.9947 |
| 天王星 | 84.021 | 19.218 | 7059.5 | 7097.8 | 0.9946 |
| 海王星 | 164.77 | 30.110 | 27149 | 27298 | 0.9945 |
問題1-1-1
ケプラーの第3法則は,公転周期 \(T\) の2乗と公転軌道半径 \(a\) の3乗のグラフが傾き1の直線になることで確認できます.しかし,極端な値の大小のために,左図の普通のグラフは適当でなく,右図の両対数グラフを使う必要があります.
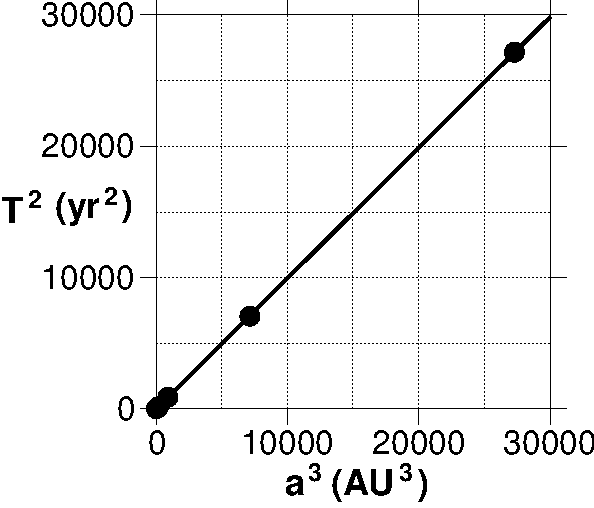
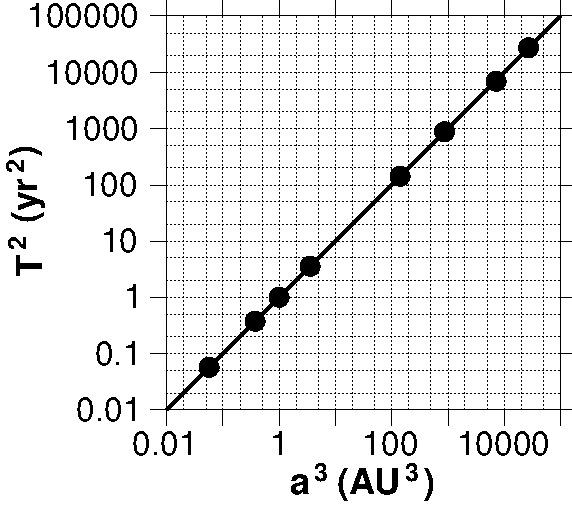
実は両対数グラフを使用すれば, \(T\) と \(a\) を直接プロットすることで(2乗や3乗をせずに),ケプラーの第3法則を確認できます.上の表に示した8つの惑星のデータをプロットし,得られた直線の傾きから \(T^2/a^3\) が一定であることを示しなさい.(→ 両対数グラフ用紙)
問題1-1-2
18世紀に提唱された,チチウス・ボーデの法則は惑星の平均軌道半径が単純な数列, \(a_n=0.4+0.3\times 2^n\),で表現できるとしたものです.但し, \(n\) は水星を \(n\) = -∞ とし,金星の \(n\) = 0 から1ずつ増やします.あくまで経験則ですが,歴史的には火星(\(n\) = 2)と木星(\(n\) = 4)の間に \(n\) = 3 の空席があったところ,ちょうどその場所に小惑星ケレスが発見された経緯があります.
実際,火星と木星の軌道は大きく離れていて,その間に存在する小惑星帯は,何らかの原因で(例えば木星の重力の影響)惑星への成長が止まったと考えられています.ここでは,原作の式とは異なりますが,軌道半径 \(a_n\) が次の等比数列に従うとして,小惑星ケレスの軌道半径を数列に含める場合と除外する場合でどちらが尤もらしいかを見ることにします. \[ a_n = a_0 p^n. \] 但し, \(a_0\) と \(p\) は定数です.片対数グラフを使用して,次の表の \(n\) と \(a_n\) をそれぞれ横軸と縦軸にとって,2つの場合をプロットし比較しなさい.(→ 片対数グラフ用紙)
| 惑星 | 水星 | 金星 | 地球 | 火星 | ケレス | 木星 | 土星 | 天王星 | 海王星 |
| \(n\) (ケレス除外) | 1 | 2 | 3 | 4 | - | 5 | 6 | 7 | 8 |
| \(n\) (ケレス含む) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| \(a_n\) (au) | 0.3871 | 0.7233 | 1 | 1.524 | 2.768 | 5.203 | 9.555 | 19.22 | 30.11 |
問題1-1-3
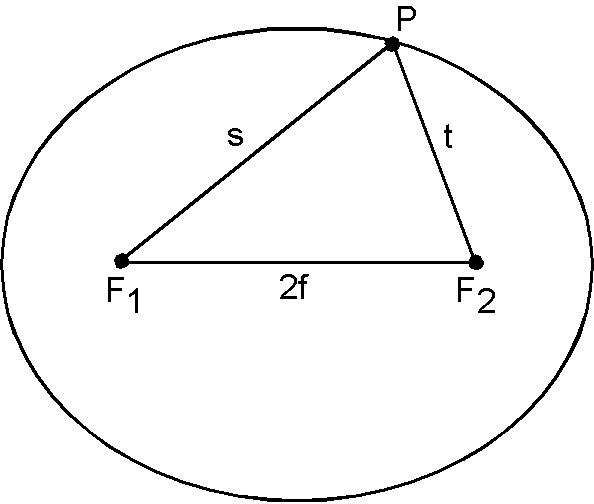
右図は楕円の作図法の1つを示します.2つの焦点 F\(_1\) と F\(_2\) からの距離の和が一定になるように点 P を動かすと,その軌跡が楕円となります.
- (1) 2焦点間の距離を 2\(f\) とし, \(a\) を定数として, \[ s + t = 2a \] の条件で作図した楕円の方程式は \[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \quad \left(b = \sqrt{a^2 - f^2}\right). \] で表されることを示しなさい.
- (2) 上の方程式の \(a\) と \(b\) はそれぞれ楕円の長半径と短半径になります.点 P と焦点との距離(\(s\) または \(t\))の平均は長半径 \(a\) に等しいことを導きなさい.即ち,太陽と惑星の平均距離は楕円軌道の長半径に等しくなります.