ロドリゲスの回転公式と回転行列
ベクトル表現の回転公式(本文の式(7))の導出
図(左)は OP で表わされるベクトル \({\bf r}\) が単位ベクトル \({\bf u}\) の方向の OQ の回りに角 \(\theta\) 回転する様子で,回転後のベクトル \({\bf r'}\) は OP' です.図(右)は \({\bf u}\) を真上から見た様子で, QP と QP' をベクトル \({\bf d}\) と \({\bf d'}\) とします.ベクトル積 \({\bf u}\times{\bf d}\) は \({\bf u}\) と \({\bf d}\) に垂直で QPP' のなす平面内にあります.
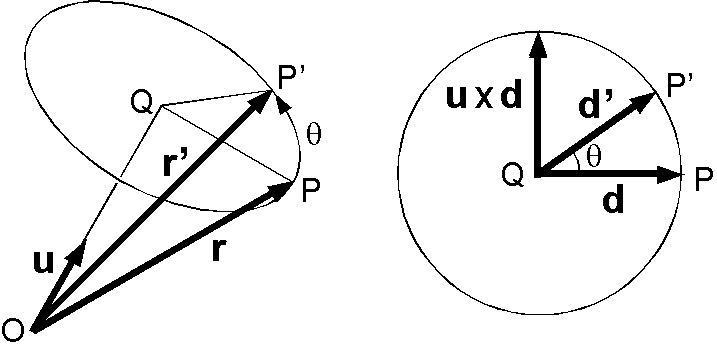
図(左)から, \begin{equation} {\bf r'} = \overrightarrow{\mathsf{OQ}} + \overrightarrow{\mathsf{QP'}}. \label{eq01} \end{equation} OQ は \({\bf r}\) の \({\bf u}\) への射影ですので, \begin{equation} \overrightarrow{\mathsf{OQ}} = ({\bf r}\cdot{\bf u}){\bf u}. \label{eq02} \end{equation} 図(右)のベクトル \({\bf d}\) は,図(左)の QP を OP と OQ で表わして, \begin{eqnarray} {\bf d} & = & \overrightarrow{\mathsf{QP}} = \overrightarrow{\mathsf{OP}} - \overrightarrow{\mathsf{OQ}}, \nonumber \\ & = & {\bf r} - ({\bf r}\cdot{\bf u}){\bf u}. \label{eq03} \end{eqnarray} 図(右)で, \(|{\bf d}|=|{\bf d'}|=|{\bf u}\times{\bf d}|\) であり, \({\bf d}\) と \({\bf u}\times{\bf d}\) は垂直ですので, \begin{eqnarray*} \overrightarrow{\mathsf{QP'}} & = & {\bf d'}, \\ & = & \cos\theta{\bf d} + \sin\theta({\bf u}\times{\bf d}). \end{eqnarray*} これに式 (3) を代入し, \({\bf u}\times{\bf u}=0\) に注意して変形すると, \begin{equation} \overrightarrow{\mathsf{QP'}} = \cos\theta{\bf r} - \cos\theta({\bf r}\cdot{\bf u}){\bf u} + \sin\theta({\bf u}\times{\bf r}), \label{eq04} \end{equation} となります.式 (2) と (4) を (1) に代入して,次のロドリゲスの回転公式を得ます. \begin{equation} {\bf r'} = (1-\cos\theta)({\bf r}\cdot{\bf u}){\bf u} + \cos\theta{\bf r} + \sin\theta({\bf u}\times{\bf r}). \label{eq05} \end{equation}
回転行列の導出
まず,直交座標系 x-y-z における基底ベクトル \({\bf e_1}\), \({\bf e_2}\), \({\bf e_3}\) を式 (5) に従って回転させ,回転後の基底ベクトル \({\bf f_1}\), \({\bf f_2}\), \({\bf f_3}\) とします.そして,次式に従って回転行列を決定します. \begin{equation} A = \left(\begin{array}{ccc} {\bf f_1} & {\bf f_2} & {\bf f_3} \end{array}\right) = \left(\begin{array}{ccc} f_{1x} & f_{2x} & f_{3x} \\ f_{1y} & f_{2y} & f_{3y} \\ f_{1z} & f_{2z} & f_{3z} \end{array}\right). \label{eq06} \end{equation} 式 (5) の \({\bf r}\) に \({\bf e_1}=(1,0,0)\) を代入し,次のベクトルの内積と外積の公式, \[ {\bf a}\cdot{\bf b} = \left(\begin{array}{c} a_x \\ a_y \\ a_z \end{array}\right) \cdot \left(\begin{array}{c} b_x \\ b_y \\ b_z \end{array}\right) = \left(\begin{array}{c} a_xb_x \\ a_yb_y \\ a_zb_z \end{array}\right), \quad {\bf a}\times{\bf b} = \left(\begin{array}{c} a_x \\ a_y \\ a_z \end{array}\right) \times \left(\begin{array}{c} b_x \\ b_y \\ b_z \end{array}\right) = \left(\begin{array}{c} a_yb_z-a_zb_y \\ a_zb_x-a_xb_z \\ a_xb_y-a_yb_x \end{array}\right). \] を利用して計算すると \({\bf r'}\) として \({\bf f_1}\) は次のようになります. \begin{eqnarray*} \left(\begin{array}{c} f_{1x} \\ f_{1y} \\ f_{1z} \end{array}\right) & = & (1-\cos\theta)u_x\left(\begin{array}{c}u_x \\ u_y \\ u_z\end{array}\right) + \cos\theta\left(\begin{array}{c}1 \\ 0 \\ 0\end{array}\right) + \sin\theta\left(\begin{array}{c}0 \\ u_z \\ -u_y\end{array}\right), \\ & = & \left(\begin{array}{l} u_xu_x(1-\cos\theta)+\cos\theta \\ u_yu_x(1-\cos\theta)+u_z\sin\theta \\ u_zu_x(1-\cos\theta)-u_y\sin\theta \end{array}\right). \end{eqnarray*} 同様にして, \({\bf e_2}\) と \({\bf e_3}\) から \({\bf f_2}\) と \({\bf f_3}\) を求め,式 (6) から回転行列は次のようになります. \[ \left(\begin{array}{lll} u_xu_x(1-\cos\theta)+\cos\theta & u_xu_y(1-\cos\theta)-u_z\sin\theta & u_xu_z(1-\cos\theta)+u_y\sin\theta \\ u_yu_x(1-\cos\theta)+u_z\sin\theta & u_yu_y(1-\cos\theta)+\cos\theta & u_yu_z(1-\cos\theta)-u_x\sin\theta \\ u_zu_x(1-\cos\theta)-u_y\sin\theta & u_zu_y(1-\cos\theta)+u_x\sin\theta & u_zu_z(1-\cos\theta)+\cos\theta \end{array}\right). \]