４-１ 地震のマグニチュード

マグニチュードとエネルギー： 地震のマグニチュード \(M\) は地震そのものの規模を表わす量で，ある地点での揺れの程度を表わす震度とは異なります．歴史的には，震央から 100 km 離れた標準地震計の記録の最大振幅の常用対数を取ってマグニチュードとしました．しかし，常に標準地震計が震央から 100 km の位置にあることはないので，実際には震央からの距離や地震計の種類によって補正をします．また，地震波の種類によっても地震波記録の振幅は異なり，後述のようにマグニチュードには幾つか種類があります．しかし，ここでは一般的に地震のマグニチュードと地震のエネルギーの関係を最初に説明します．

地震のエネルギーとマグニチュードの関係を求めるには，マグニチュードが決定された地震について，その震源を囲む球を通過した地震波のエネルギーを計算します．そのためには，全ての周波数の地震波エネルギーを時間と空間について積分する必要があり，膨大な計算となるようです．このこのようにして得られた地震のエネルギー \(E\) とマグニチュード \(M\) の関係は次の経験式で表わされます． \begin{equation} \log_{10}E = 4.8 + 1.5 M. \label{eq01} \end{equation} 但し， \(E\) の単位はジュール（J = N m）です．この式からは，マグニチュードの差が 2 の地震のエネルギーは 10³ 倍異なることが分かります．そのため一般には，地震のエネルギーはマグニチュードが 1 増えると約 30 倍になると言われています（正確には， 10^1.5 = 10√10 = 31.6 倍）．

マグニチュードと発生頻度： 地震の規模が小さいほど発生頻度が高いことは経験的に知られていて，微小地震（1 ≤ \(M\) < 3）や極微小地震（\(M\) < 1）といわれる小さい地震は頻繁に発生しています．ある一定地域である一定期間にマグニチュードが \(M\) と \(M+dM\) の間の地震が発生する回数を， \[ n(M)dM, \] で表わすとき， \(n(M)\) は次式で表わされることが経験的に知られています． \begin{equation} \log_{10}n(M) = a - bM. \label{eq02} \end{equation} また，この式を \(M\) から \(\infty\) まで \(M\) で積分することで，マグニチュードが \(M\) 以上の地震について積算した発生回数 \(N(M)\) は次の経験式で表わされ，同じ傾き \(b\) の直線となります． \begin{equation} \log_{10}N(M) = A - bM. \label{eq03} \end{equation} これらの式はグーテンベルグ-リヒターの式といわれ， \(a\)， \(A\)， \(b\) は地域に特有な定数で，一般に \(b\) は 1 に近い値となります．

下図に日本付近（緯度：25°N-48°N，経度：125°E-150°E）の \(M\) ≥ 5 の地震について，マグニチュードが \(M\) 以上の地震の積算発生回数 \(N(M)\) （黒丸）と， \(dM\) = 0.1 毎の発生回数 \(n(M)dM\) （白丸）を示します．左図は 1961〜2010 年の 50 年間，右図は 2011 年の１年間についてです．データは米国地質調査所のデータベース（USGS Search Earthquake Catalog）からダウンロードしました． 50 年間の左図ではデータ数 5254 で， \(N(M)\) も \(n(M)\) もその常用対数は完全ではないもののほぼ直線になります． \(b\) の値もおよそ１となり，グーテンベルグ-リヒター則は成立しているようです．しかし，右図の東北地方太平洋沖地震の発生した 2011 年では， \(M\) = 7 の上下でグラフの傾きがかなり異なります．このことは，千年に１度の巨大地震が発生した 2011 年は地震活動としては特殊な年だったためと考えられます．そもそも， 2011 年のデータ数が 866 と異常に多いことは，巨大地震後の余震が頻発したためです．

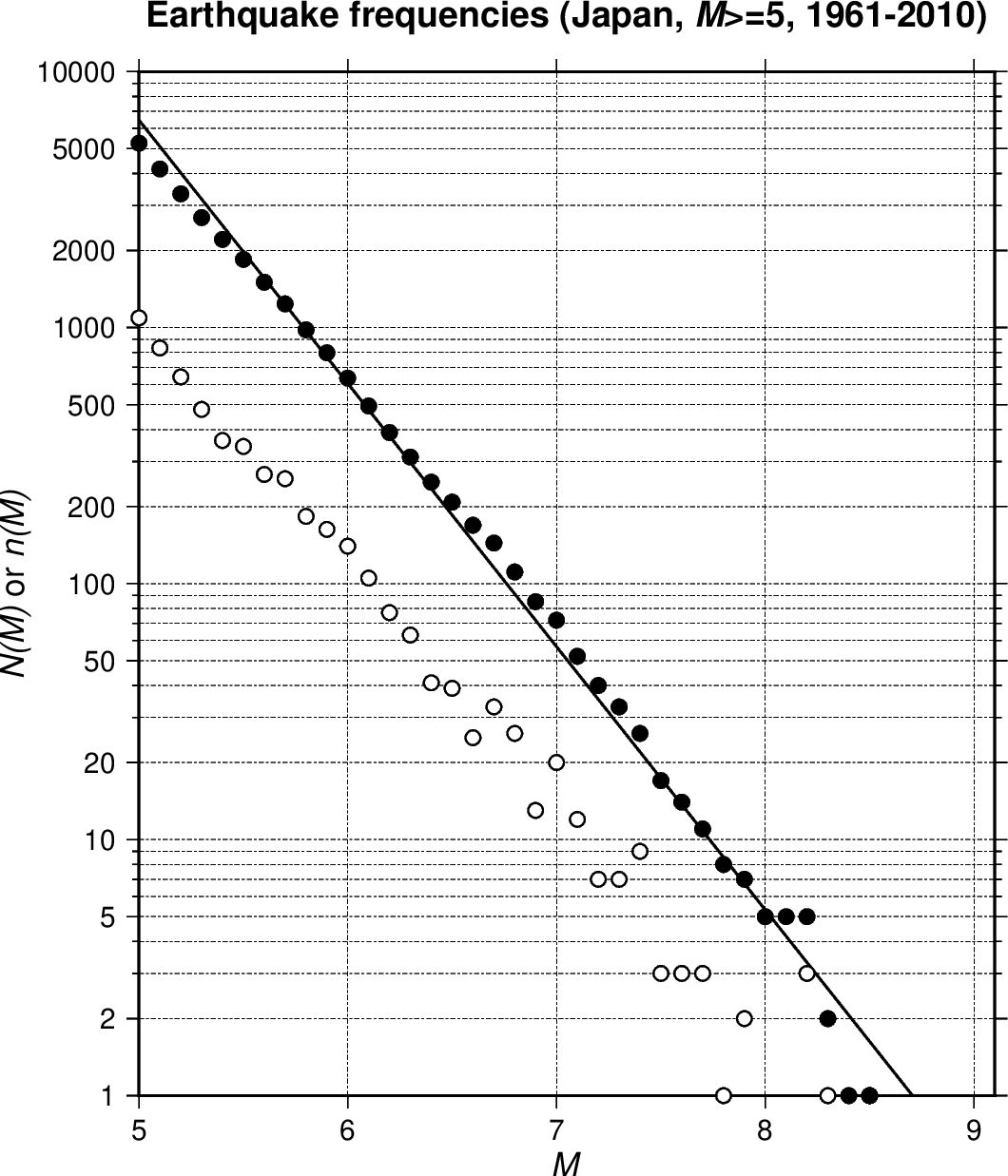
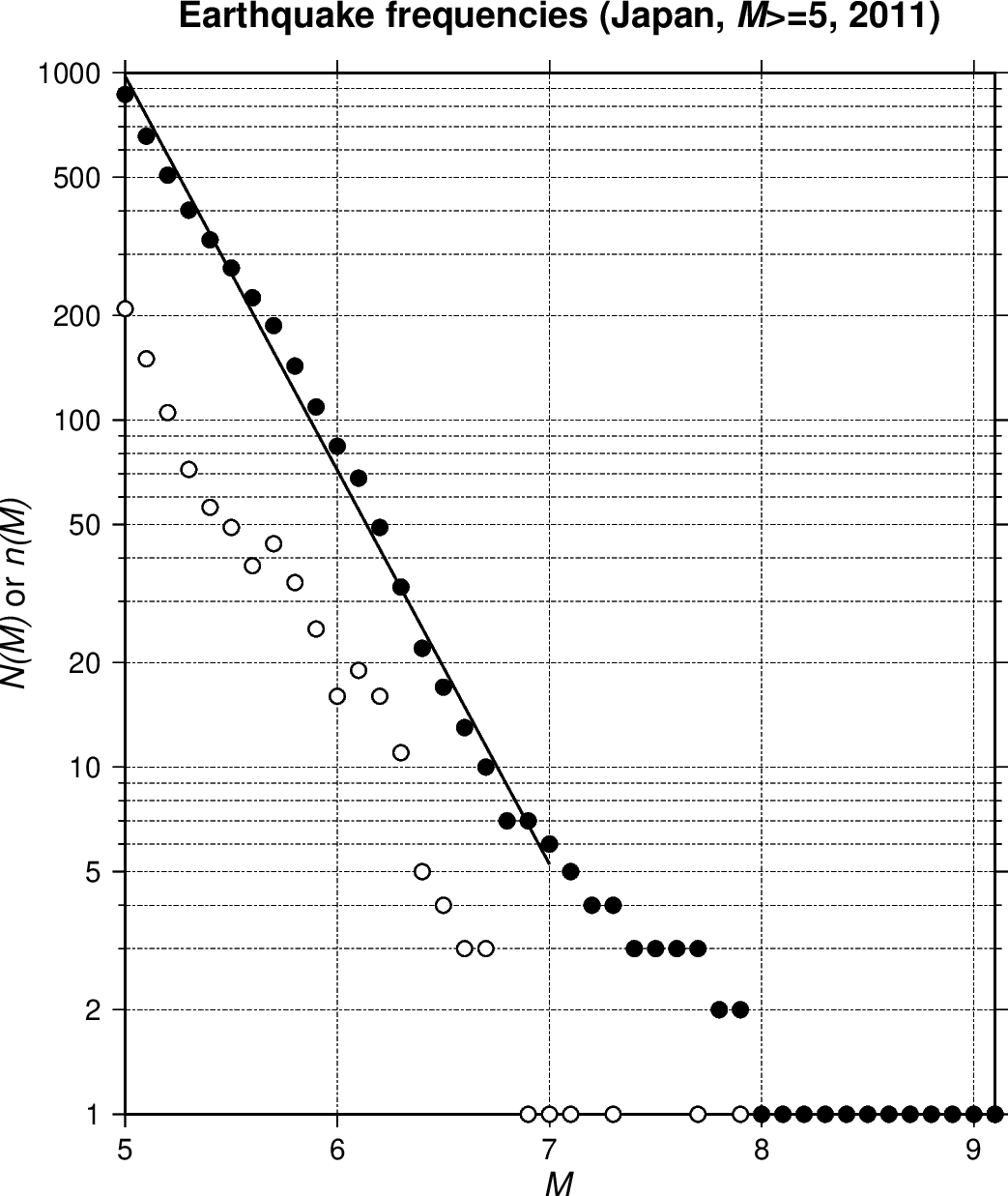
上図は \(M\) ≥ 5 の地震を全て含みます．しかし専門レベルでは，地震をその種類や発生する深さなどで分類した上で，グーテンベルグ-リヒター則を研究します．この経験則は提唱されてから何十年も経ちますが，カオスやフラクタルとの関わりで現在も地震学者や数理科学者により研究が続いています．

↑ ページ冒頭

モーメント・マグニチュード： 地震のマグニチュードは冒頭に記したように，地震波記録の最大振幅の常用対数から決定し，使用する地震波の種類によりいくつか種類があります．代表的なマグニチュードは表面波マグニチュード \(M_S\) と実体波マグニチュード \(m_b\) です．地震波は通常P波，S波，表面波の順に到達します．表面波マグニチュードは周期 20 s 程度の表面波から決定するのに対して実体波マグニチュードは周期 5 s 以下の実体波であるP波やS波から決定します．しかし，具体的な計算式は幾通りか提案されているようで，気象庁の発表する気象庁マグニチュード \(M_J\) もその一つです．

しかし，これらのマグニチュードは地震の規模が大きくなると，相応の大きな値を示さなくなり，地震学ではマグニチュードが飽和すると表現します．その理由は，断層運動の規模が大きいほど地震波は長周期の波を多く含むようになり，短い周期の地震波からは地震の規模を正しく決定できなくなるためです．そのため，実体波マグニチュードではおよそ 6 で，表面波マグニチュードと気象庁マグニチュードでは約 8.2 で頭打ちとなります．そこで，現在では Kanamori (1977) により提唱されたモーメント・マグニチュード \(M_W\) が広く使用されています．これは大きい地震にも適用でき，気象庁も顕著な地震については気象庁マグニチュードと併記しています．例えば東北地方太平洋沖地震（2011年）については， \(M_J\) = 8.4 に対して \(M_W\) = 9.0 と報告されています．

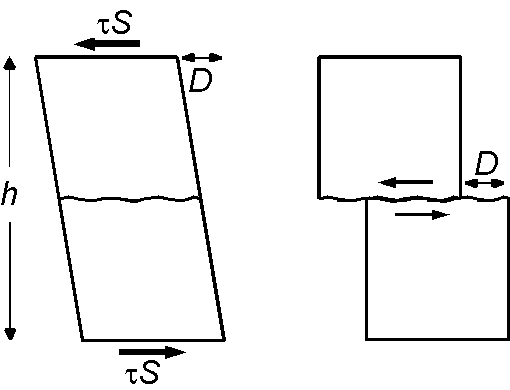
ここで地震発生時の断層運動の力のモーメントについて考えます．図（左）は面積が \(S\) の断層の近傍がずれ応力 \(\tau\) により横方向に距離 \(D\) 歪んでいる様子です．応力は単位面積当たりの力ですので，力 \(\tau S\) が断層に偶力として働いています．このとき断層近傍のずれ歪み \(\epsilon\) は「→ ４-４ 弾性体の力学と断層運動」の式 (3) より次式で表わされます． \[ \epsilon = \frac{1}{2}\frac{D}{h}. \] また，ずれ応力 \(\tau\) は同じページの式 (4) より，岩石の剛性率を \(\mu\) として次式となります． \[ \tau = 2\mu\epsilon = \mu\frac{D}{h}. \] 偶力のモーメントは「力\(\times\)腕の長さ」で次式となり，これが地震モーメント \(M_0\) です（単位は N m）． \begin{eqnarray} M_0 & = & \mu\frac{D}{h}S\times h, \nonumber \\ & = & \mu DS. \label{eq04} \end{eqnarray} この式の \(D\) と \(S\) は地震観測から正確に求められるので， \(M_0\) は地震の規模を直接表わす量です．

さらに，地震モーメントから地震で放出されるエネルギー \(W_0\) を見積もることができます．断層がずれ動くときの平均のずれ応力を \(\bar\tau\) とすると，エネルギーは「力\(\times\)作用距離」の次式で与えられます． \[ W_0 = \bar\tau S\times D. \] 平均応力 \(\bar\tau\) は弾性体理論などから地震前後の応力 \(\tau_0\) と \(\tau_1\) の差の半分になることが示されています． \(\Delta\sigma=\tau_0-\tau_1\) をストレス・ドロップといい， \(\bar\tau=\Delta\sigma/2\) と式 (4) から \(W_0\) は次式となります． \[ W_0 = \frac{1}{2}\Delta\sigma SD = \frac{\Delta\sigma}{2\mu}M_0. \] ストレス・ドロップは多くの地震でほぼ一定の 3 MPa であり，典型的な岩石の剛性率を 30 GPa としてこの式に代入すると，地震で放出されるエネルギーは次式となります（単位は J）． \begin{equation} W_0 \approx 0.5\times10^{-4}M_0. \label{eq05} \end{equation} 式 (5) は地震の放出するエネルギーを直接表わす量ですが，対数スケールで表わすと便利です．そこで次のように，従来のエネルギーとマグニチュードの関係を表わす式 (1)， \(\log_{10}E=4.8+1.5M\)，の \(E\) に式 (5) の \(W_0\) を代入して得られる \(M\) をモーメント・マグニチュード \(M_W\) としました． \begin{eqnarray} \log_{10}(0.5\times10^{-4}M_0) & = & 4.8 + 1.5 M_W, \nonumber \\ \log_{10}M_0 & = & 9.1 + 1.5 M_W. \label{eq06} \end{eqnarray} 式 (6) によるモーメント・マグニチュード \(M_W\) は従来の表面波マグニチュード \(M_S\) などと滑らかに繋がり，かつ巨大地震でも飽和しないスケールです．

↑ ページ冒頭

問題４-１-１

（１） 地震のエネルギー \(E\) とマグニチュード \(M\) との間には， \[ \log_{10}E = 4.8 + 1.5 M, \] の関係があります．但し， \(E\) の単位は J (joule) です．では，２つの地震のマグニチュードを \(M_1\) と \(M_2\)，エネルギーを \(E_1\) と \(E_2\) とするとき，エネルギーの比 \(E_2/E_1\) をマグニチュードの差 \(M_2-M_1\) で表わす式を導きなさい．この式を使って， \(M\) が２大きくなると \(E\) は千倍になることを示しなさい．

（２） \(M\) = 9.1 の東北地方太平洋沖地震（2011年）のエネルギーは \(M\) = 6.9 の兵庫県南部地震（1995年）のエネルギーの何倍か?（マグニチュードは米国地質調査所による \(M_W\) です）

（３） ある理論によると地震のエネルギーは，大きさが水平方向 \(l\times l\)，深さ方向 \(l/3\) の直方体で表わされる余震域の含むエネルギーに等しく， \[ E = 62.2\times l^3, \] で与えられるそうです．ただし，距離の単位は m でエネルギーの単位は J です．この式と上記の \(E\) と \(M\) の関係式を用いて，余震域の広さ \(S\)（単位は m²）とマグニチュード \(M\) の次の関係式を導きなさい． \[ \log_{10}S = 2 + M. \] また，余震域を正方形とするとき，余震域の１辺の長さは \(M\) = 7 と \(M\) = 9 の地震でそれぞれ何 km か?

→ 問題４-１-１ 解説

問題４-１-２

（１） 本文の式 (2) で示したグーテンベルグ-リヒターの式の \(n(M)\) は \(dM\) を掛けることで，マグニチュードが \(M\) から \(M+dM\) の地震の発生回数になります．ここでは \(dM\) は小さな一定値として省略し， \(n(M)\) をマグニチュード \(M\) の地震が一定期間に発生する回数と見なし， \(n\) で表わします．

そこで，日本付近の地震について，マグニチュード \(M\) の地震が 100 年間に発生する回数 \(n\) は \(b\) を 1 として次式で表わされるとします． \[ \log_{10}n = a - M. \] ２つの地震について，発生回数の比 \(n_2/n_1\) をマグニチュードの差 \(M_1-M_2\) で表す式を導きなさい．

では， \(M\) = 8.0 の南海地震（1946年）の発生頻度を 120 年に１度と仮定すると， \(M\) = 7.3 の兵庫県南部地震（1995年）は何年に１度発生することになるか? \(M\) = 9.0 の東北地方太平洋沖地震（2011年）についてはどうか? 但し，これらの地震で \(a\) は共通と仮定します．

（２） 次の \(n(M)\) を与える式， \[ \log_{10}n(M) = a - bM, \] を用いて， \(n(M)\) を \(M\) = \(M\) から \(M\) = \(\infty\) まで積分することで，マグニチュードが \(M\) 以上の地震の積算発生回数 \(N(M)\) が次式で与えられることを示しなさい． \[ \log_{10}N(M) = A - bM. \] 但し，定数 \(A\) は次式で表わされます (式中，\(\ln\) は \(\log_e\) です)． \[ A = a - \log_{10}(b\ln 10). \]

→ 問題４-１-２ 解説

問題４-１-３

ある地域で一定期間に発生したマグニチュードが \(M_1\) から \(M_2\) の地震の総エネルギーは，エネルギーとマグニチュードの関係式，及び発生頻度とマグニチュードの関係式から \[ E(M){\small \left|\frac{dN(M)}{dM}\right|}dM, \] を \(M_1\) から \(M_2\) まで \(M\) で積分して見積もることができます（\(E(M)n(M)dM\) の積分でも同じです）．

（１） 本文の図で示した，日本付近の 1961 年から 50 年間の地震発生頻度を次の式で近似します． \[ \log_{10}N(M) = 9.0 - 1.0M, \] \(M\) を 5.0 から期間の最大値 8.5 まで積分してエネルギーの総量 \(E_T\) と年平均値を計算しなさい．

（２） 期間中最大の地震は 1963 年に択捉島付近で発生した \(M_W\) = 8.5 の地震です．この地震１回のエネルギーを問い (1) で求めた 50 年間の地震エネルギーの総量と比較しなさい．また， \(M_W\) = 9.1 の東北地方太平洋沖地震についてはどうか．

→ 問題４-１-３ 解説

参考文献：

• Kanamori, H., The energy release in great earthquakes, J. Geophys. Res., 82, 2981-2987, 1977.
• USGS Search Earthquake Catalog (アメリカ地質調査所 地震検索カタログ), URL: https://earthquake.usgs.gov/earthquakes/search/, Earthquake Hazards Program, USGS (United States Geological Survey).

↑ ページ冒頭   → 次ページ