偏心双極子:ガウス係数と双極子の地球中心からのずれ
地球表面には電流がないと仮定すると,地球の磁場(磁束密度)はスカラーポテンシャル \(W\) の微分として与えられます. \[ {\bf B} = -\nabla W. \] \(\nabla\cdot{\bf B}=0\) であるので,ポテンシャル \(W\) はラプラス(Laplace)の方程式を満たします. \[ \nabla^2 W = 0. \] この方程式を球座標で解くと,地球内部起源の磁場に対する \(W\) は球関数を用いて次式で表されます. \begin{equation} W = a\sum_{n=1}^\infty\sum_{m=0}^n\left(\frac{a}{r}\right)^{n+1}P_n^m(\cos\theta)(g_n^m\cos m\phi + h_n^m\sin m\phi), \label{eq01} \end{equation} ここに \(a\) は地球半径, \((r,\theta,\phi)\) は観測点の球座標 (\(r\geq a\)), \(P_n^m(\cos\theta)\) は擬正規化されたシュミット(Schmidt)球関数(ルジャンドル陪関数)です. \(g_n^m\) と \(h_n^m\) はガウス係数と呼ばれ,磁束密度の単位(T)で表します. 1830 年代にカール・フリードリヒ・ガウス(Carl Friedrich Gauss)が初めて最小二乗法を用いてガウス係数を決定し,地磁気がほとんど内部起源であることと地球中心の(地心)双極子磁場に近いことを示しました. 1900 年からは,ガウス係数は国際標準地球磁場(International Geomagnetic Reference Field, IGRF)として5年毎に報告されています.次の表に, IGRF-13 (IAGA Working Group V-MOD, 2020) による 2020 年のガウス係数を \(n\)=1 から 3 まで nT (10\(^{-9}\)T) の単位で示しました.
| \(n\) | \(m\) | \(g\) | \(h\) | \(n\) | \(m\) | \(g\) | \(h\) | \(n\) | \(m\) | \(g\) | \(h\) | ||||
| 1 | 0 | -29404.8 | 0.0 | 2 | 0 | -2499.6 | 0.0 | 3 | 0 | 1363.2 | 0.0 | ||||
| 1 | 1 | -1450.9 | 4652.5 | 2 | 1 | 2982.0 | -2991.6 | 3 | 1 | -2381.2 | -82.1 | ||||
| 2 | 2 | 1677.0 | -734.6 | 3 | 2 | 1236.2 | 241.9 | ||||||||
| 3 | 3 | 525.7 | -543.4 |
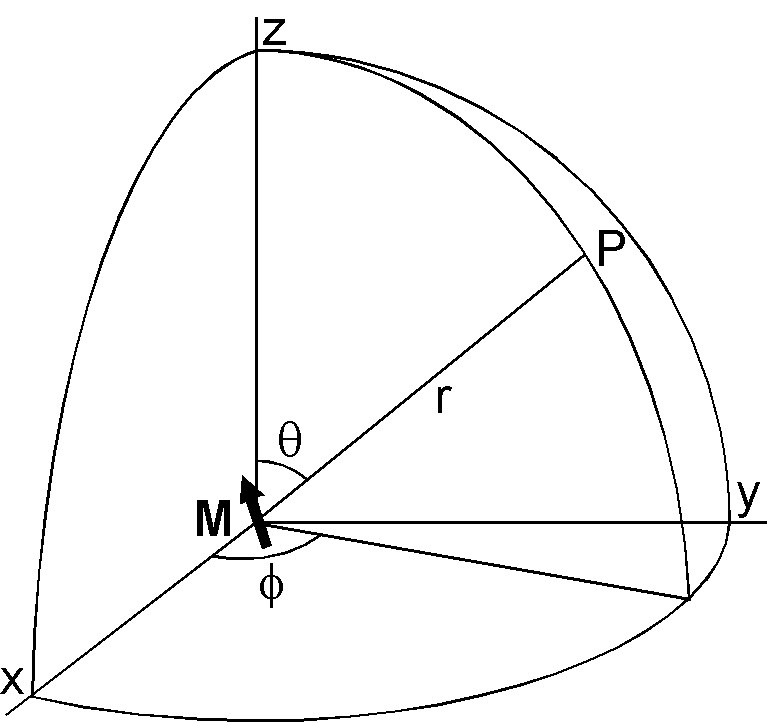
この表から分かるように, \(n\)=1 の項の地磁気への寄与は高次の項よりずっと大きいです. \(n\)=1 の項が地心双極子磁場に相当することは次のようにして示されます.右図のような地心双極子を考えると,磁気ポテンシャルは, \begin{eqnarray*} W & = & \frac{\mu_0}{4\pi}\frac{{\bf M}\cdot{\bf r}}{r^3} \\ & = & \frac{\mu_0}{4\pi r^2}\left(M_x\sin\theta\cos\phi + M_y\sin\theta\sin\phi + M_z\cos\theta\right), \end{eqnarray*} となります.ここで,\(P_1^0(\cos\theta)\)=\(\cos\theta\), \(P_1^1(\cos\theta)\)=\(\sin\theta\) を考慮すると, \eqref{eq01} において \(n\)=1 の項は, \[ W = \frac{a^3}{r^2}(g_1^0 \cos\theta + g_1^1 \sin\theta \cos\phi + h_1^1 \sin\theta \sin\phi), \] となり,これら2つのポテンシャルの式を比較することで, \(n\)=1 の項と地心双極子との関係が次のように求まります. \begin{equation} g_1^0 = \frac{\mu_0}{4\pi a^3}M_z, \quad g_1^1 = \frac{\mu_0}{4\pi a^3}M_x, \quad h_1^1 = \frac{\mu_0}{4\pi a^3}M_y. \label{eq02} \end{equation} よって,地磁気は地心双極子と高次の非双極子項を合計することで表しますが,これは数学の扱いとして便利だからです.この非双極子項を双極子の地球中心からのずれとして表すことができれば,より直感的に地磁気を理解できます.これは偏心双極子(eccentric dipole, offset dipole)と呼ばれます.
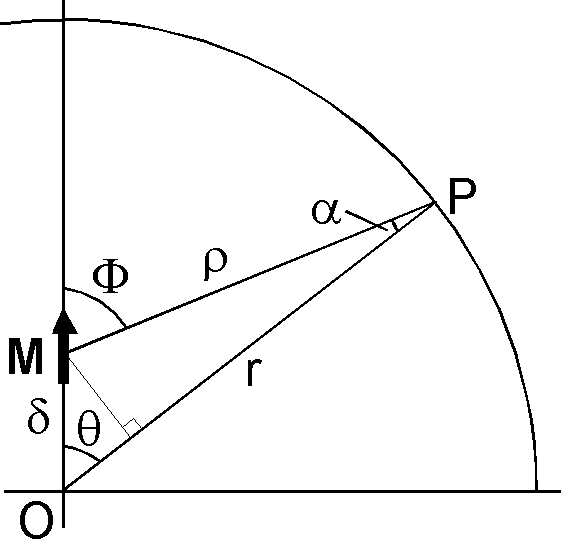
以下の偏心双極子の易しい解説は Lowrie (2011) に基づいています.最初に右図のような,地球の自転軸に沿って微小な距離 \(\delta\) ずれた軸双極子を考えます.この双極子による観測点 P におけるポテンシャルは, \begin{equation} W = \frac{\mu_0}{4\pi}\frac{M\cos\Phi}{\rho^2}, \label{eq03} \end{equation} となり,ここに \(\Phi\) と \(\rho\) は \(\theta\) と \(r\) に対して次の関係があります. \begin{eqnarray*} \cos\Phi & = & \cos(\theta+\alpha) = \cos\theta\cos\alpha - \sin\theta\sin\alpha, \\ \rho^2 & = & r^2 + \delta^2 -2r\delta\cos\theta. \end{eqnarray*} \(\delta\) と \(\alpha\) は微少量なので,次の近似が成立します. \[ \sin\alpha = \frac{\delta\sin\theta}{\rho} \approx \frac{\delta\sin\theta}{r}, \quad \cos\alpha \approx 1. \] これらの近似を用いると次式を得ます. \[ \cos\Phi \approx \cos\theta - \frac{\delta}{r}\sin^2\theta, \qquad \rho^2 \approx r^2\left(1 - \frac{2\delta}{r}\cos\theta\right). \] これらの近似式を \eqref{eq03} へ代入すると \(W\) は以下のように変形されます. \begin{eqnarray*} W & \approx & \frac{\mu_0}{4\pi}M\left(\cos\theta - \frac{\delta}{r}\sin^2\theta\right)\left/\left(r^2\left(1 - \frac{2\delta}{r}\cos\theta\right)\right)\right., \\ & \approx & \frac{\mu_0 M}{4\pi r^2}\left(\cos\theta - \frac{\delta}{r}\sin^2\theta\right)\left(1 + \frac{2\delta}{r}\cos\theta\right), \\ & \approx & \frac{\mu_0 M}{4\pi r^2}\left(\cos\theta - \frac{\delta}{r}\sin^2\theta + \frac{2\delta}{r}\cos^2\theta\right), \\ & \approx & \frac{\mu_0 M}{4\pi r^2}\cos\theta + \frac{\mu_0 M\delta}{4\pi r^3}(3\cos^2\theta - 1), \\ & \approx & \frac{\mu_0 M}{4\pi r^2}P_1^0(\cos\theta) + \frac{\mu_0 M\delta}{2\pi r^3}P_2^0(\cos\theta). \end{eqnarray*} 最後の式を \eqref{eq01} における \(n\)=1 と 2 の項と比較すると次式を得ます. \begin{equation} g_1^0 = \frac{\mu_0}{4\pi a^3}M, \qquad g_2^0 = \frac{\mu_0 \delta}{2\pi a^4}M. \label{eq04} \end{equation} よって,軸双極子が自転軸に沿って微小距離ずれると, \(g_2^0\) 項が現れます.
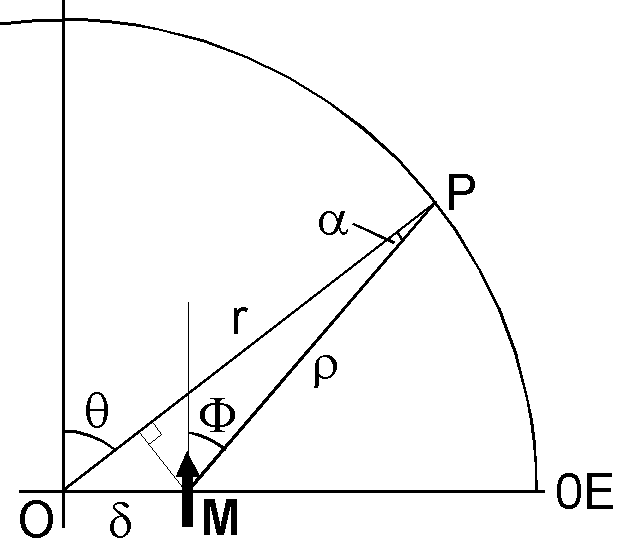
双極子が赤道面内でずれる場合も同様にして扱えます.右図は軸双極子が赤道面内で微小距離 \(\delta\) だけ 0°E の方向へずれた様子を示します.この場合の \(\Phi\), \(\theta\), \(\rho\), \(r\) の関係は, \begin{eqnarray*} \cos\Phi & = & \cos(\theta-\alpha) = \cos\theta\cos\alpha + \sin\theta\sin\alpha, \\ \rho^2 & = & r^2 + \delta^2 -2r\delta\sin\theta, \end{eqnarray*} となります.また,\(\sin\alpha\) と \(\cos\alpha\) の近似は, \[ \sin\alpha = \frac{\delta\cos\theta}{\rho} \approx \frac{\delta\cos\theta}{r}, \qquad \cos\alpha \approx 1, \] となり,以下の近似式を得ます. \[ \cos\Phi \approx \cos\theta + \frac{\delta}{r}\sin\theta\cos\theta, \qquad \rho^2 \approx r^2\left(1 - \frac{2\delta}{r}\sin\theta\right). \] 結局, \eqref{eq03} のポテンシャル \(W\) は以下のように変形されます. \begin{eqnarray*} W & \approx & \frac{\mu_0}{4\pi}M\left(\cos\theta+\frac{\delta}{r}\sin\theta\cos\theta\right)\left/\left(r^2\left(1-\frac{2\delta}{r}\sin\theta\right)\right)\right., \\ & \approx & \frac{\mu_0 M}{4\pi r^2}\left(\cos\theta+\frac{\delta}{r}\sin\theta\cos\theta\right)\left(1+\frac{2\delta}{r}\sin\theta\right), \\ & \approx & \frac{\mu_0 M}{4\pi r^2}\left(\cos\theta+\frac{3\delta}{r}\sin\theta\cos\theta\right), \\ & \approx & \frac{\mu_0 M}{4\pi r^2}P_1^0(\cos\theta) + \frac{\sqrt{3}\mu_0 M\delta}{4\pi r^3}P_2^1(\cos\theta). \end{eqnarray*} 最後の式を, \eqref{eq01} の \(n\)\(\leq\)2 の項(\(\phi\)=0)と比較すると次式を得ます. \begin{equation} g_1^0 = \frac{\mu_0}{4\pi a^3}M, \qquad g_2^1 = \frac{\sqrt{3}\mu_0 \delta}{4\pi a^4}M \label{eq05} \end{equation} 上の図では,偏心双極子も観測点もグリニッジ子午面内にあります.しかし,より詳細な導出(次ページ)によれば, 0°E と 90°E の方向へのずれにより,それぞれ \(g_2^1\) と \(h_2^1\) の項が現れることが示されます.一般に,軸双極子が赤道面内で微小距離ずれると, \(g_2^1\) と \(h_2^1\) の項が現れると結論できます.
参考文献:
- IAGA Working Group V-MOD, International Geomagnetic Reference Field: IGRF-13 is released, 2020. (URL: https://www.ngdc.noaa.gov/IAGA/vmod/igrf.html)
- Lowrie, W., A Student's Guide to Geophysical Equations, 281 pp., Cambridge University Press, Cambridge, 2011.