ビンガム分布
我々が観測する古地磁気方向は時々伸長した分布をしていますが,通常は360度対称な分布を仮定してフィッシャー統計で解析します.単位球上の伸長した分布を記述する統計の一つが Bingham (1974) により提出されました.ビンガム統計は非常に難解な理論ですが,数値計算の方法を用いれば古地磁気学への応用は容易です (Onstott, 1980).ビンガム統計の数値計算法に対する簡単な解説は Tanaka (1999) にもあります.
ある程度の分散を持った \(N\) 個の古地磁気方向を仮定して,それぞれの方向を単位ベクトル \({\bf L}_i=(x_i,y_i,z_i)\) で表します.まず最初に,データ点の分布を次の行列 \({\bf T}\) で解析します. \begin{equation} {\bf T} = \left(\begin{array}{ccc} \sum_{i=1}^N x_i^2 & \sum_{i=1}^N x_i y_i & \sum_{i=1}^N x_i z_i \\ \sum_{i=1}^N x_i y_i & \sum_{i=1}^N y_i^2 & \sum_{i=1}^N y_i z_i \\ \sum_{i=1}^N x_i z_i & \sum_{i=1}^N y_i z_i & \sum_{i=1}^N z_i^2 \end{array}\right). \label{eq01} \end{equation} 主成分解析と同様に行列 \({\bf T}\) の固有値 \(\tau_1\), \(\tau_2\), \(\tau_3\) (\(\tau_1 \leq \tau_2 \leq \tau_3\), \(\tau_1 + \tau_2 + \tau_3 = N\)) と対応する固有ベクトル \({\bf t}_1\), \({\bf t}_2\), \({\bf t}_3\) からデータ点の分布の構造が分かります.典型的な中程度のバラつきを持った古地磁気方向の場合 (\(\tau_1 \leq \tau_2 \ll \tau_3\)),\({\bf t}_3\) が平均方向となり,\(\tau_2\) と \(\tau_1\) の差が大きいほど伸長した分布を示し \({\bf t}_2\) が伸長の方向となります.帯状で同一平面上の分布の場合は (\(\tau_1 \ll \tau_2 \leq \tau_3\)),\({\bf t}_1\) が帯の平面に対する極を与えます.
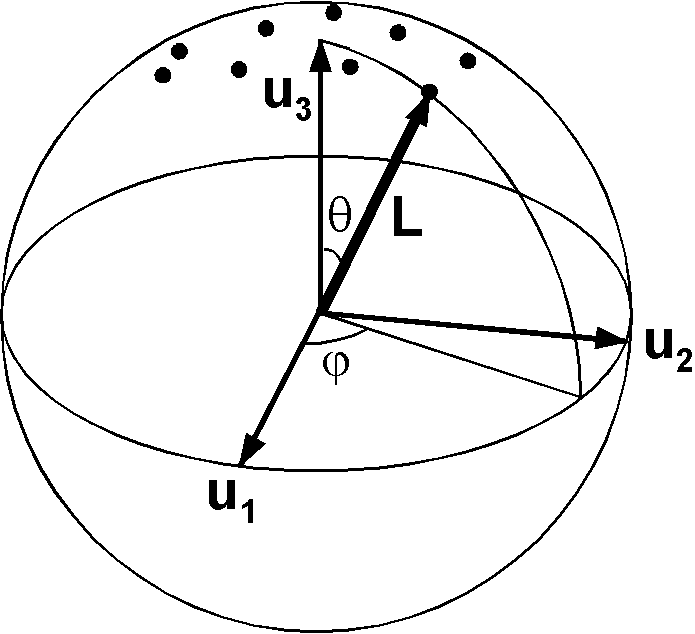
ビンガム分布の確率密度は次式で与えられます. \[ b = \frac{1}{4\pi d(k_1,k_2,k_3)} e^{k_1({\bf L}\cdot{\bf u}_1)^2} e^{k_2({\bf L}\cdot{\bf u}_2)^2} e^{k_3({\bf L}\cdot{\bf u}_3)^2}, \] ここに \({\bf u}_1\), \({\bf u}_2\), \({\bf u}_3\) は真の固有ベクトル,\(k_1\), \(k_2\), \(k_3\) は集中度パラメータ,\(d(k_1,k_2,k_3)\) は正規化係数です.一方,\(\tau_1\), \(\tau_2\), \(\tau_3\) と \({\bf t}_1\), \({\bf t}_2\), \({\bf t}_3\) がそれぞれ真の固有値と固有ベクトルの最良推定値であることが示されています.また,\(k_3\) をゼロとしても一般性を失わないことも示されました.図のような座標系,\(\theta\) と \(\varphi\),を取ればビンガム分布関数は次式のように簡単化されます. \begin{equation} b(\theta,\varphi) = \frac{1}{4\pi d(k_1,k_2)} e^{(k_1\cos^2\varphi + k_2\sin^2\varphi)\sin^2\theta}, \label{eq02} \end{equation} ここに \(d(k_1,k_2)\) は \begin{equation} d(k_1,k_2) = \frac{1}{4\pi} \int_0^{2\pi}\int_0^\pi e^{(k_1\cos^2\varphi + k_2\sin^2\varphi)\sin^2\theta} \sin\theta d\theta d\varphi, \label{eq03} \end{equation} で与えられます.\eqref{eq03}の解析解は存在しないので,\(d(k_1,k_2)\) は数値的に決定します.
\(k_1\) と \(k_2\) の最尤推定値(maximum likelihood estimate)はビンガム分布の次の尤度関数を最大にすることで得られます. \begin{eqnarray*} F & = & \log \prod_{i=1}^N \frac{1}{4\pi d(k_1,k_2)} e^{(k_1\cos^2\varphi_i + k_2\sin^2\varphi_i)\sin^2\theta_i} \\ & = & -N\log 4\pi - N\log d(k_1,k_2) + k_1\sum_{i=1}^N \cos^2\varphi_i\sin^2\theta_i + k_2\sum_{i=1}^N \sin^2\varphi_i\sin^2\theta_i. \end{eqnarray*} 最後の2つの項に関しては,\(\cos\varphi_i\sin\theta_i\) と \(\sin\varphi_i\sin\theta_i\) はそれぞれ固有ベクトル \({\bf u}_1\) と \({\bf u}_2\) の方向の \({\bf L}_i\) の成分です.固有ベクトルに沿った成分の二乗の和は対応する固有値に等しいので,尤度関数は次のようになります. \begin{equation} F = -N\log 4\pi - N\log d(k_1,k_2) + k_1\tau_1 + k_2\tau_2. \label{eq04} \end{equation} 条件\eqref{eq03}のもとで尤度関数\eqref{eq04}を最大にする \(k_1\) と \(k_2\) を見つけることはプログラミングの最大ルーチンを利用すれば難しくはありません.Bingham (1974) はまた,固有ベクトル \({\bf t}_3\) の回りの 95\(\%\) 信頼限界半径が次式で与えられることを示しました. \begin{equation} \alpha_{31} = 2.45\sigma_{31}, \quad \alpha_{32} = 2.45\sigma_{32}, \label{eq05} \end{equation} ここに \(\alpha_{31}\) と \(\alpha_{32}\) はそれぞれ \({\bf t}_1\) と \({\bf t}_2\) 方向の半径で,\(\sigma_{ij}\) は次式で与えられます. \begin{equation} \sigma_{ij}^2 = \frac{1}{2(k_i - k_j)(\tau_i - \tau_j)}. \label{eq06} \end{equation}
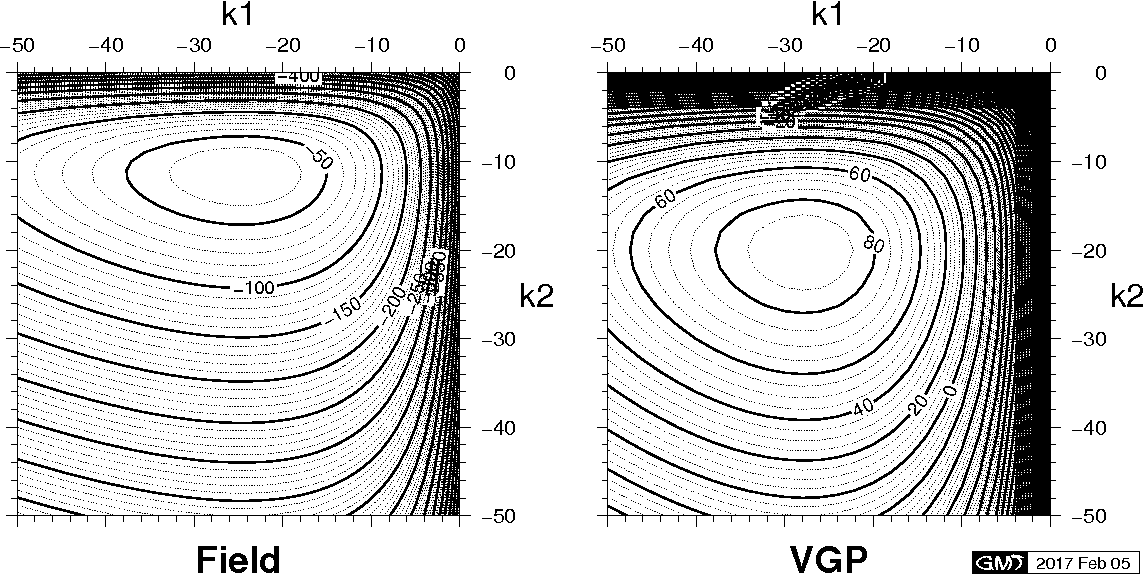
過去 500 万年間にハワイ島で観測された古地磁気方向の 324 のデータ(→図を表示)をビンガム統計で解析しました.ビンガム分布の \(\sin^2\theta\) 依存性のために両極性のデータを同時に解析することができました.結果をまとめたテーブルからは,磁場方向の分布が子午線方向に沿って伸長しているのに対して,VGP の分布はほとんど円状であることが分かります.最後の図はハワイデータの解析における \(k_1\) と \(k_2\) に対する等しい \(F\) のコンター図で,いかなる局所的な最大値も見られません.
| \(k_1\) | \(k_2\) | \(\tau_1\) | \(\tau_2\) | \(\alpha_{31}\) | \(\alpha_{32}\) | |
| Field | -24.6 | -11.3 | 6.74 | 15.12 | 1.16° | 1.74° |
| VGP | -27.8 | -20.0 | 5.95 | 8.34 | 1.08° | 1.28° |
ビンガム統計の解析における \(k_1\) と \(k_2\) に対する等しい \(F\) のコンター図.
参考文献:
- Bingham, C., An antipodally symmetric distribution on the sphere, Ann. Statistics, 2, 1201-1225, 1974.
- Onstott, T. C., Application of the Bingham distribution function in paleomagnetic studies, J. Geophys. Res., 85, 1500-1510, 1980.
- Tanaka, H., Circular asymmetry of the paleomagnetic directions observed at low latitude volcanic sites, Earth Planets Space, 51, 1279-1286, 1999. (→doi:10.1186/BF03351601)