円近似: 古典的 Kasa (1976) の方法
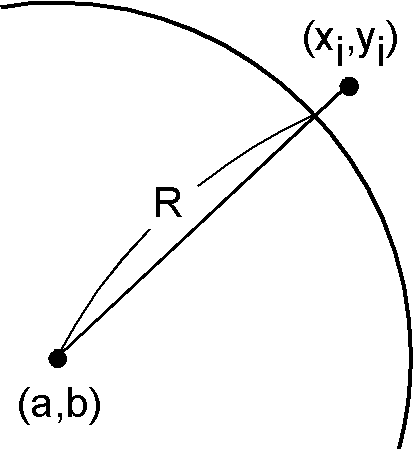中心 \((a,b)\)，半径 \(R\) の円による \(n\) 個の観測点 \((x_i,y_i)\) (\(i=1,\cdots,n\)) の近似を考えます．観測点の円弧からの"幾何学的"距離は，
\[ d_i = r_i -R, \]
で表されます．ここに，
\[ r_i = \sqrt{ (x_i - a)^2 + (y_i - b)^2 }, \]
です．幾何学的方法では，次式で表される距離 \(d_i\) の二乗の合計を最小にする \(a\)， \(b\)， \(R\) を決定します．
\[
\sum_{i=1}^n d_i^2 = \sum_{i=1}^n \left(\sqrt{(x_i-a)^2 + (y_i-b)^2} - R\right)^2.
\]
しかし，この方法は非線形問題のため解くのはかなり困難です．ここでは，正確さは劣りますが，より単純で広く使用されている"代数学的"方法を紹介します．このページでは古典的 Kasa (1976) の方法を，次ページでは改良された Taubin (1991) の方法を扱います．
Kasa (1976) の方法では， 代数学的距離を次式で定義します． \[ f_i = r_i^2 - R^2. \] 最小にする量は， \begin{eqnarray*} {\cal F_K} & = & \sum_{i=1}^n f_i^2, \\ & = & \sum_{i=1}^n (x_i^2 + y_i^2 - 2ax_i - 2by_i + a^2 + b^2 - R^2)^2 \end{eqnarray*} となります．ここで，次の新しいパラメーターを導入します． \begin{eqnarray} B & = & -2a, \nonumber \\ C & = & -2b, \label{eq01} \\ D & = & a^2 + b^2 - R^2. \nonumber \end{eqnarray} 記号 "\(A\)" を使用しないのは次ページの理論との整合性のためです．すると， \[ {\cal F_K} = \sum_{i=1}^n (z_i + Bx_i + Cy_i + D)^2, \] 但し， \[ z_i = x_i^2 + y_i^2. \] です． \( \partial {\cal F_K}/\partial B = \partial {\cal F_K}/\partial C = \partial {\cal F_K}/\partial D =0 \) より次式を得ます． \begin{equation} \begin{array}{ccccccc} M_{xx}B & + & M_{xy}C & + & M_xD & = & -M_{xz} \\ M_{xy}B & + & M_{yy}C & + & M_yD & = & -M_{yz} \\ \label{eq02} M_xB & + & M_yC & + & nD & = & -M_z \end{array} \end{equation} 但し， \(M_x = \sum_{i=1}^n x_i, M_{xx} = \sum_{i=1}^n x_i^2, M_{xy} = \sum_{i=1}^n x_i y_i\) 等です． LU 分解法等の数値的方法で \eqref{eq02} を解けば， \(a\)， \(b\)， \(R\) は \eqref{eq01} で与えられます.
残念ながら，この方法は時々答えとして小さな \(R\) を与える傾向があります． Al-Sharadqah and Chernov (2009) によると， \[ f_i = (r_i - R)(r_i + R) = d_i(2R + d_i) \approx 2Rd_i. \] 故に， Kasa 法は次式を最小にすることになります． \[ {\cal F_K} \approx 4 R^2 \sum_{i=1}^n d_i^2, \] そして，この方法はしばしば \(\sum_{i=1}^n d_i^2\) よりも \(R^2\) を最小にするようです．これを改良するには， \[ {\cal F} = \frac{1}{4R^2} {\cal F_K} \] を最小にすると良く，次頁で示します．
参考文献:
- Al-Sharadqah, A., and N. Chernov, Error analysis for circle fitting algorithms, Elect. J. Stat., 3, 886-911, 2009.
- Kasa, I., A curve fitting procedure and its error analysis, IEEE Trans. Inst. Meas., 25, 8-14, 1976.