古地磁気学と岩石磁気学の基礎

主成分解析

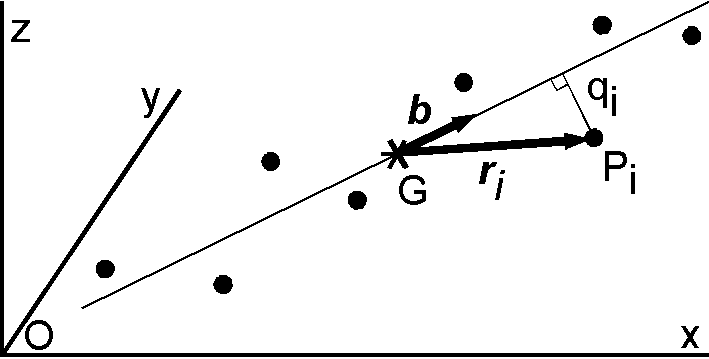慣性モーメント最小によるベストフィットの直線． 古地磁気データの解析には主成分解析 (principal component analysis; PCA) が有効です (Kirschvink, 1980)．図は主成分解析の残留磁化方向の決定への応用を示し，データ点は段階消磁における残留磁化ベクトルの端点を表します．残留磁化方向はデータ点の慣性モーメントの合計 (\(I\)) が最小になる軸として求められます．各データ点 \(P_i\) に単位質量を仮定すると， \(I\) は次式で与えられます． \begin{eqnarray*} I & = & \sum_{i=1}^N 1 \times q_i^2 \\ & = & \sum_{i=1}^N \{|{\bf r}_i|^2 - ({\bf b}\cdot{\bf r}_i)^2\} = \sum_{i=1}^N |{\bf r}_i|^2 - \sum_{i=1}^N ({\bf b}\cdot{\bf r}_i)^2 \end{eqnarray*} ここに \(q_i\) は \(P_i\) の軸からの距離， \({\bf r}_i\) は重心 \(G\) から各データ点 \(P_i\) へのベクトル， \({\bf b}\) は軸に沿った単位ベクトルです． \(I\) を最小にする \({\bf b}\) を求めることは第２項を最大にする \({\bf b}\) を求めることと同値です．ここでは通常の主成分解析に従って，条件 \(|{\bf b}|=1\) のもとで \(\frac{1}{N}\sum_{i=1}^N({\bf b}\cdot{\bf r}_i)^2\) を最大にすることを考えます．ラグランジュ乗数 \(\lambda\) を用いて次式を最大にします． \[ {\cal F} = \frac{1}{N}\sum_{i=1}^N({\bf b}\cdot{\bf r}_i)^2 - \lambda({\bf b}\cdot{\bf b}-1) \] ここで次の行列 \({\bf A}\) を導入します． \[ {\bf A} = \left(\begin{array}{lll} \frac{1}{N}\sum_{i=1}^N(x_i-\bar x)^2 & \frac{1}{N}\sum_{i=1}^N(x_i-\bar x)(y_i-\bar y) & \frac{1}{N}\sum_{i=1}^N(x_i-\bar x)(z_i-\bar z) \\ \frac{1}{N}\sum_{i=1}^N(x_i-\bar x)(y_i-\bar y) & \frac{1}{N}\sum_{i=1}^N(y_i-\bar y)^2 & \frac{1}{N}\sum_{i=1}^N(y_i-\bar y)(z_i-\bar z) \\ \frac{1}{N}\sum_{i=1}^N(x_i-\bar x)(z_i-\bar z) & \frac{1}{N}\sum_{i=1}^N(y_i-\bar y)(z_i-\bar z) & \frac{1}{N}\sum_{i=1}^N(z_i-\bar z)^2 \end{array}\right) \] 但し， \({\bf r}_i = (x_i-\bar x,y_i-\bar y,z_i-\bar z)\) です． \({\bf A}\) を用いて \({\cal F}\) は次式で与えられます． \[ {\cal F} = {^t{\bf b}} {\bf A} {\bf b} - \lambda(^t{\bf b}{\bf b} - 1). \] \(\partial{\cal F}/\partial{\bf b}=2{\bf A}{\bf b}-2\lambda{\bf b}=0\) として次式を得ます． \begin{equation} {\bf A}{\bf b} = \lambda{\bf b}. \label{eq01} \end{equation}

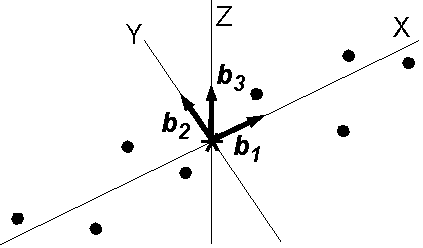
３つの固有ベクトルと主軸．

固有値問題である方程式 \eqref{eq01} を解くと，３つの固有値 (\(\lambda_1 \geq \lambda_2 \geq \lambda_3\)) とそれぞれの固有ベクトル (\({\bf b}_1,{\bf b}_2,{\bf b}_3\)) が求まります．これらの結果は総じて，データ点の分布形状を推測するのに役立ちます．図のような直線状の残留磁化の場合は (\(\lambda_1 \gg \lambda_2 \geq \lambda_3\))， \({\bf b}_1\) がベストフィットの残留磁化方向を与え， \(\lambda_1\) は \({\bf b}_1\) 方向の分散 (\(\sigma_1^2\)) となります．実際， \(X\) 軸を \({\bf b}_1\) に沿って取り，原点 \(O\) を重心 \(G\) に取れば， \(X\) の分散は次のように \(\lambda_1\) となります． \begin{eqnarray*} \sigma_1^2 & = & \frac{1}{N}\sum_{i=1}^N X_i^2 = \frac{1}{N}\sum_{i=1}^N ({\bf b}_1\cdot{\bf r}_i)^2 \\ & = & {^t{\bf b}}_1{\bf A}{\bf b}_1 = {^t{\bf b}}_1(\lambda_1{\bf b}_1) = \lambda_1(^t{\bf b}_1{\bf b}_1) = \lambda_1. \end{eqnarray*} \(Y\) 軸と \(Z\) 軸をそれぞれ \({\bf b}_2\) と \({\bf b}_3\) に沿って取ると，異なる軸の共分散はゼロになります．実際， \(X\) と \(Y\) の共分散（\(\gamma_{12}\)）は次のようにゼロとなります． \begin{eqnarray*} \gamma_{12} & = & \frac{1}{N}\sum_{i=1}^N X_i Y_i = \frac{1}{N}\sum_{i=1}^N ({\bf b}_1\cdot{\bf r}_i)({\bf b}_2\cdot{\bf r}_i) \\ & = & {^t{\bf b}}_1{\bf A}{\bf b}_2 = {^t{\bf b}}_1(\lambda_2{\bf b}_2) = \lambda_2(^t{\bf b}_1{\bf b}_2) = 0. \end{eqnarray*} 固有値は対応する固有ベクトルの軸に沿った標準偏差の二乗 (\(\sigma^2\)) ですので， Kirschvink (1980) はそれらをベストフィットの直線の誤差を表すのに使用することを提唱しました．この目的のために，次の MAD (Maximum Angular Deviation) が導入されました． \begin{equation} MAD = \arctan\left(\frac{\sqrt{\sigma_2^2+\sigma_3^2}}{\sigma_1}\right) = \arctan\left(\sqrt{\frac{\lambda_2+\lambda_3}{\lambda_1}}\right). \label{eq02} \end{equation}

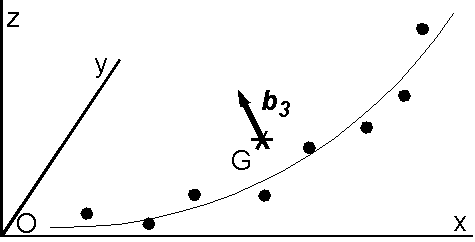
３番めの固有ベクトルとベストフィットの平面．

残留磁化が２成分を含む場合は，図のように段階消磁に従って残留磁化ベクトルの端点が平面上の円弧のような軌跡を辿ることがしばしばあります．このような場合は１つの固有値が他の２つの固有値に比べて格段に小さく (\(\lambda_3 \ll \lambda_2 \leq \lambda_1\))，最小の固有値 \(\lambda_3\) に対応する固有ベクトル \({\bf b}_3\) が平面に対する極を表します．このような場合に平面の極の誤差を表す角度として， Kirschvink (1980) は次の MAD を使用することを提唱しました． \begin{equation} MAD = \arctan\left(\sqrt{\frac{\sigma_3^2}{\sigma_2^2}+\frac{\sigma_3^2}{\sigma_1^2}}\right) = \arctan\left(\sqrt{\frac{\lambda_3}{\lambda_2}+\frac{\lambda_3}{\lambda_1}}\right). \label{eq03} \end{equation}

参考文献:

↑ ページ冒頭