流線関数による磁力線
静磁場 \({\bf H}\) は磁気ポテンシャル \(W\) の勾配として与えられます. \begin{equation} {\bf H} = -\nabla W. \label{eq01} \end{equation} 2次元の場合を考えると, \({\bf H}\) は等ポテンシャルの曲線(\(W = \mathsf{const.}\))に垂直です.それ故, \(W\) に直交するスカラー関数 \(\phi\) が分かれば,等しい \(\phi\) の曲線(\(\phi = \mathsf{const.}\))が磁力線となります. \(\phi\) は流線関数(stream function)と呼ばれます.ここでは,その原理の平易な入門と磁気双極子の磁力線への応用を解説します.
真空中の静磁場を考えると次式が成立します. \[ \nabla\cdot{\bf H} = (1/\mu_0)\nabla\cdot{\bf B} = 0. \] この式を2次元直交座標に適用すると次式を得ます. \[ \nabla\cdot{\bf H} = \frac{\partial H_x}{\partial x} + \frac{\partial H_y}{\partial y} = 0. \] この式に \eqref{eq01} を代入,即ち, \(H_x=-\partial W/\partial x\) と \(H_y=-\partial W/\partial y\) を代入すると,次式となります. \begin{equation} \frac{\partial}{\partial x}\left(\frac{\partial W}{\partial x}\right) = -\frac{\partial}{\partial y}\left(\frac{\partial W}{\partial y}\right). \label{eq02} \end{equation} ここで,次式を満たす別なスカラー関数 \(\phi\) を導入します. \[ \frac{\partial W}{\partial x} = \frac{\partial \phi}{\partial y}, \qquad \frac{\partial W}{\partial y} = -\frac{\partial \phi}{\partial x}. \] 新しいスカラー関数 \(\phi\) は \eqref{eq02} を満たし, \(\nabla\phi\cdot\nabla W=0\) なのでポテンシャル \(W\) に直交します. \({\bf H}\) もまた \(\phi\) で与えることができます.即ち, \(H_x=-\partial\phi/\partial y\), \(H_y=\partial\phi/\partial x\) となります.
次に2次元の極座標系の場合を考えます; \[ \nabla\cdot{\bf H} = \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2H_r\right) + \frac{1}{r\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta H_\theta\right) = 0. \] よって,次式を得ます. \[ \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2H_r\right) = -\frac{1}{r\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta H_\theta\right). \] これに \eqref{eq01} を代入,即ち, \(H_r=-\partial W/\partial r\) と \(H_\theta=-(1/r)\partial W/\partial\theta\) を代入すると,次式となります. \begin{equation} \frac{\partial}{\partial r}\left(r^2\frac{\partial W}{\partial r}\right) = -\frac{1}{\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial W}{\partial\theta}\right). \label{eq03} \end{equation} \eqref{eq03} を吟味すると,流線関数 \(\phi\) は次式を満たす必要があることが分かります. \begin{equation} r^2\frac{\partial W}{\partial r} = \frac{1}{\sin\theta}\frac{\partial\phi}{\partial\theta}, \qquad \sin\theta\frac{\partial W}{\partial\theta} = -\frac{\partial\phi}{\partial r}. \label{eq04} \end{equation} \(\phi\) と \(W\) の直交性は次のようにして確認されます. \begin{eqnarray*} \nabla\phi\cdot\nabla W & = & \frac{\partial\phi}{\partial r}\frac{\partial W}{\partial r} + \frac{1}{r}\frac{\partial\phi}{\partial\theta}\frac{1}{r}\frac{\partial W}{\partial\theta} \\ & = & \frac{1}{r^2\sin\theta}\frac{\partial\phi}{\partial r}\frac{\partial\phi}{\partial\theta} - \frac{1}{r^2\sin\theta}\frac{\partial\phi}{\partial\theta}\frac{\partial\phi}{\partial r} = 0. \end{eqnarray*} また, \({\bf H}\) は次式のように \(\phi\) を用いることでも表すことができます. \begin{equation} H_r = -\frac{\partial W}{\partial r} = -\frac{1}{r^2\sin\theta}\frac{\partial\phi}{\partial\theta}, \qquad H_\theta = -\frac{1}{r}\frac{\partial W}{\partial\theta} = \frac{1}{r\sin\theta}\frac{\partial\phi}{\partial r}. \label{eq05} \end{equation}
ここからは上の結果を2次元の極座標系の原点に置かれた磁気双極子に応用します.\(\theta=0\) 方向を向いた磁気双極子 \({\bf m}\) の磁気ポテンシャル \(W\) は次式で与えられます. \begin{equation} W = \frac{m}{4\pi}\frac{\cos\theta}{r^2}. \label{eq06} \end{equation} 磁気ポテンシャル \eqref{eq06} を \(\phi\) が満たすべき \eqref{eq04} へ代入すると, \(\phi\) が次式で与えられることが分かります. \begin{equation} \phi = -\frac{m}{4\pi}\frac{\sin^2\theta}{r}. \label{eq07} \end{equation} 得られた \(\phi\) と \(W\) が直交することは \(\nabla\phi\cdot\nabla W\) がゼロになることから確かめられます. \eqref{eq07} を \eqref{eq05} へ代入することで \(H_r\) と \(H_\theta\) は次のようになります. \begin{equation} H_r = -\frac{1}{r^2\sin\theta}\frac{\partial\phi}{\partial\theta} = \frac{m}{2\pi}\frac{\cos\theta}{r^3}, \qquad H_\theta = \frac{1}{r\sin\theta}\frac{\partial\phi}{\partial r} = \frac{m}{4\pi}\frac{\sin\theta}{r^3}. \label{eq08} \end{equation} これらの式は磁気ポテンシャル \(W\) から導かれたものと同じです.
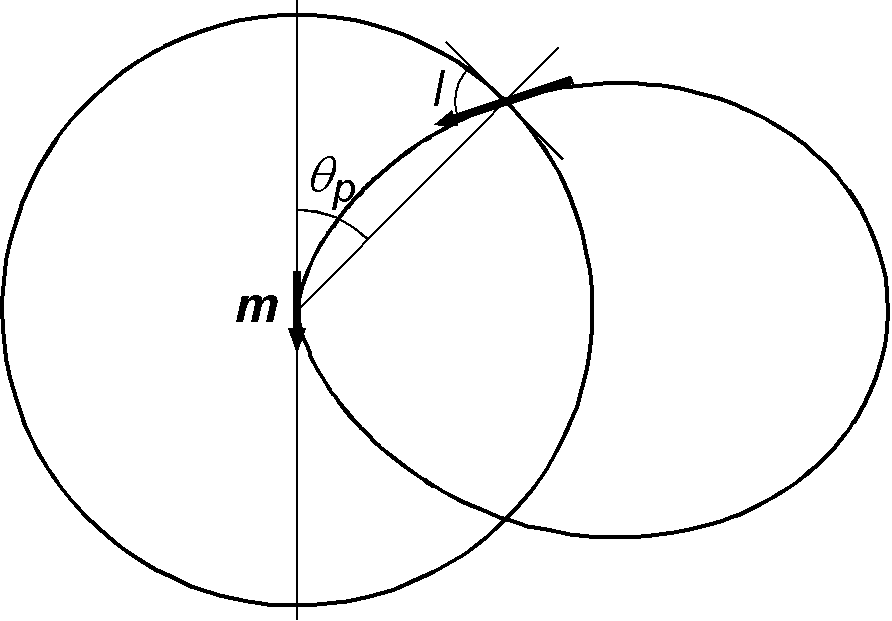
双極子磁場の磁力線は \eqref{eq07} を使用し, \(\phi\) を一定にしたまま \(\theta\) に対して \(r\) をプロットすれば容易に描くことができます.但し,磁力線は磁束密度 \({\bf B}\) を考慮して描かれるべきです.図のように,半径 1 の球面上で余緯度が \(\theta_p\) の点における磁束密度の密度関数 \(f(\theta_p)\) を考えます(\(m\) は地球の磁場を模して負とします).磁束密度は真空中では \(|{\bf H}|\) に比例するので, \eqref{eq08} で \(r=1\) と置いて, \[ f(\theta_p) \propto \sqrt{1 + 3\cos^2\theta_p}. \] 球面上では磁力線が傾いていることを考慮して,密度関数は磁束密度に \(\sin I\) を掛けたものとなります.ここに \(I\) は磁力線と球の接線との角度(inclination, 伏角)です.よって, \[ f(\theta_p) \propto \sin I \sqrt{1 + 3\cos^2\theta_p}. \] \(I\) は \(\theta_p\) と \(\tan I = 2\cot\theta_p\) という関係にあるので \(\sin I\) は次のようになります. \[ \sin I = 2\cos\theta \left/ \sqrt{1 + 3\cos^2\theta_p}\right.. \] 結局,磁束密度の密度関数は \(\cos\theta_p\) に比例することになります; \[ f(\theta_p) \propto \cos\theta_p. \] 磁束密度の密度関数 \(f(\theta_p)\) の累積分布関数 \(F(\theta_p)\) は次のようになります. \begin{eqnarray} F(\theta_p) & = & \int_0^{\theta_p}\cos\theta d\theta \left/ \int_0^{\pi/2}\cos\theta d\theta\right. \nonumber \\ & = & \sin\theta_p \quad (0 \leq \theta_p \leq \pi/2). \label{eq09} \end{eqnarray} 最後の式 \eqref{eq09} が示すことは,余緯度の 0° から 90° の間に \(N\) 本の磁力線を描く場合は \(i\) 番目の磁力線が次式で与えられる \(\theta_{p_i}\) の点を通るようにするということです. \[ \sin\theta_{p_i} = i/N. \quad (i=0, 1, \cdots, N-1) \]