古地磁気学と岩石磁気学の基礎

フィッシャー分布

古地磁気の方向は複数の岩石残留磁化方向の測定から決定しますが，測定結果には一定のばらつきがあります．これらの残留磁化方向を解析する統計学が Fisher (1953) によって提出されました．単位球面上の観測点の確率密度は次式で与えられます． \begin{equation} f(\theta) = \frac{\kappa}{4 \pi \sinh \kappa} e^{\kappa \cos \theta} \label{eq01} \end{equation} ここに \(\theta\) は真の方向からの角度であり， \(\kappa\) は精密度パラメーター（precision parameter）と呼ばれ，ゼロ（一様分布）から \(+\infty\) （一点集中）までの値を取ります． \(\kappa/4\pi\sinh\kappa\) の項は正規化係数です．実際， \eqref{eq01} を単位球の表面で積分すると次のように 1 になります． 単位球面上に投影した残留磁化ベクトルの偏角と伏角． \begin{eqnarray*} & & \int_0^{2\pi} \int_0^\pi \frac{\kappa}{4 \pi \sinh \kappa} e^{\kappa \cos \theta} \sin \theta d\theta d\varphi \\ & & = \frac{\kappa}{2\sinh \kappa}\left[-\frac{1}{\kappa}e^{\kappa \cos\theta}\right]_0^\pi \\ & & = \frac{\kappa}{e^\kappa - e^{-\kappa}}\frac{e^\kappa - e^{-\kappa}}{\kappa} = 1. \end{eqnarray*}

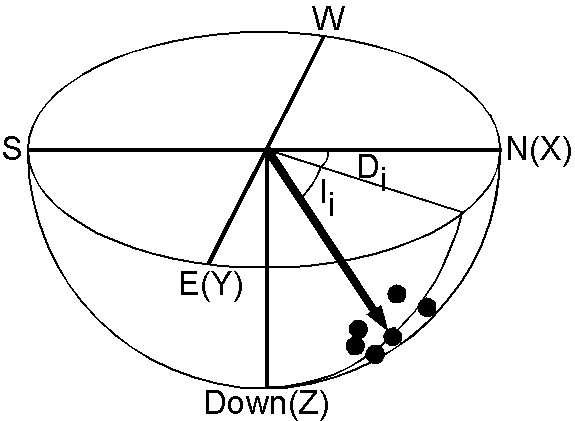
フィッシャー統計は非常に難解な理論ですが，古地磁気学への応用は単純です．偏角 \(D\) （declination）と伏角 \(I\) （inclination）を使用して，それぞれの方向は図のように単位ベクトルで表されます．真の方向の最良推定値（best estimate）は \(N\) 個の観測点のベクトル和 \({\bf R}\) （合成ベクトル, resultant vector）で与えられます． \begin{equation} {\bf R} = (\sum_{i=1}^N \cos D_i \cos I_i, \sum_{i=1}^N \sin D_i \cos I_i, \sum_{i=1}^N \sin I_i). \label{eq02} \end{equation} それ故，平均方向 \((D_m, I_m)\) は， \begin{equation} \tan D_m = \frac{R_Y}{R_X}, \quad \sin I_m = \frac{R_Z}{R}. \label{eq03} \end{equation} となります． \(\kappa\) の最良推定値 \(k\) は， \(\kappa\) > 3 のとき，次式で与えられます． \begin{equation} k = \frac{N - 1}{N - R}. \label{eq04} \end{equation} Fisher (1953) はさらに， \({\bf R}\) もまた精密度 \(\kappa R\) のフィッシャー分布に従うことを証明し，真の方向の確率 \((1 - P)\) の信頼限界の角度が次式で与えられることを示しました． \begin{equation} \cos \alpha_{(1-P)} = 1 - \frac{N-R}{R}\left[\left(\frac{1}{P}\right)^{\frac{1}{N-1}} - 1\right]. \label{eq05} \end{equation} 通常は \(P=0.05\) を取り， \eqref{eq05} は平均方向の回りの \(95\%\) 信頼限界円 \(\alpha_{95}\) （conficence circle）を表します．

角度標準偏差 \(S\) （angular standard deviation），または角度分散（angular dispersion），は次式で定義されます． \begin{equation} S^2 = \frac{1}{N-1} \sum_{i=1}^N \theta_i^2. \label{eq06} \end{equation} \(\theta \ll 1\) に対する近似式， \(\cos\theta \approx 1 - \frac{\theta^2}{2}\) ，を利用して， \eqref{eq06} は次のように近似されます． \begin{eqnarray*} S^2 & \approx & \frac{1}{N-1}\sum_{i=1}^N(2 - 2\cos\theta_i) \\ & = & \frac{1}{N-1}(2\sum_{i=1}^N 1 - 2 \sum_{i=1}^N \cos\theta_i) = 2\frac{N-R}{N-1} = \frac{2}{k}. \end{eqnarray*} それ故，大きな \(k\) に対する次の近似式を得ます． \begin{equation} S \approx \frac{81}{\sqrt{k}} \quad \mathsf{[deg.]}. \label{eq07} \end{equation}

↑ ページ冒頭

この角度はしばしば \(\theta_{63}\) と記されます．これは２次元正規分布に準じています．２次元正規分布では観測値の 63% が１標準偏差の中に含まれるからです（１次元では 68%）．このことは，次のように２次元正規分布の確率密度から示すことができます． \[ {\scriptsize \frac{1}{\sqrt{2\pi}\sigma}}e^{-x^2/2\sigma^2}{\scriptsize \frac{1}{\sqrt{2\pi}\sigma}}e^{-y^2/2\sigma^2}dxdy = {\scriptsize \frac{1}{2\pi\sigma^2}}e^{-r^2/2\sigma^2}rdrd\varphi, \] ここに， \(x=r\cos\varphi\) 及び \(y=r\sin\varphi\) です． \(r\) の分散は \(\sigma^2+\sigma^2=2\sigma^2\) ですので，確率密度を積分して， \[ \frac{1}{\sigma^2}\int_0^{\sqrt{2}\sigma}re^{-r^2/2\sigma^2}dr = \left[-e^{-r^2/2\sigma^2}\right]_0^{\sqrt{2}\sigma} = 1 - e^{-1} = 0.6321. \] この考えをフィッシャー分布に適用します．式 \eqref{eq01} を使用して， \[ \frac{\kappa}{2\sinh\kappa}\int_0^{\theta_{63}}e^{\kappa\cos\theta}\sin\theta d\theta = \frac{e^\kappa-e^{\kappa\cos\theta_{63}}}{e^\kappa-e^{-\kappa}} = 0.6321. \] この式を \(\cos\theta_{63}\) について解くと， \[ \cos\theta_{63} = 1 + \frac{\log\left(1 - 0.6321(1 - e^{-2\kappa})\right)}{\kappa} \] ここで， \(\kappa \gg 1\) と \(\theta_{63} \ll 1\) として近似すると次式が得られます． \begin{eqnarray*} 1 - \frac{\theta_{63}^2}{2} & \approx & 1 + \frac{\log 0.3679}{\kappa}, \\ \theta_{63}^2 & \approx & \frac{2}{\kappa}. \end{eqnarray*} さらに \(\kappa\) を \(k\) で近似すれば，式 \eqref{eq07} で与えられる角度標準偏差 \(S\) と同じ表現を得ます．

近似による表現は小さな \(\alpha_{95}\) に対しても有効です．式 \eqref{eq05} は以下のように近似されます． \[ 1 - \frac{\alpha_{95}^2}{2} = 1 - \frac{N-R}{R}\left(20^\frac{1}{N-1} - 1\right). \] \(x \ll 1\) に対する近似式， \(\log(1+x) \approx x\) ，を利用すると， \[ \log 20^\frac{1}{N-1} = \log\left[1 + \left(20^\frac{1}{N-1} -1\right)\right] \approx 20^\frac{1}{N-1} - 1. \] となります．この関係式を利用して次式を得ます． \[ \alpha_{95}^2 \approx \frac{2(N-R)}{R} \log 20^\frac{1}{N-1} = \frac{2(N-R)}{R(N-1)} \log 20. \] 故に， \[ \alpha_{95}^2 \approx \frac{2\log 20}{kR}. \] 最後に， \(R\) を \(N\) で近似し，小さな \(\alpha_{95}\) の次の近似式を得ます． \begin{equation} \alpha_{95} \approx \frac{140}{\sqrt{kN}} \quad \mathsf{[deg.]}. \label{eq08} \end{equation}

参考文献:

↑ ページ冒頭