問題７−２−１ 解答

プレートテクトニクスの幾何学を解くために便利な方法は模型を使用することです．プレートの配置を用紙に描きプレート境界に沿って切った紙片を実際に動かしてみると理解しやすいです．

しかし，ここではプレートに付けた目印が時間の経過でどこに移動するかを示すことで考察します．下の解答では，プレート境界付近の左と右のプレートにそれぞれ丸と四角の印を付けました．それらの印が時間経過後に移動した位置から断層の長さの変化について推測できるはずです．また，海溝では三角印の付いた側が上盤であることに留意する必要があります．なお，灰色の印は他のプレートの下に移動したことを示します．

６種類のトランスフォーム断層の断層長の変化

なお， (c) では断層の長さがゼロになった時点で，海嶺と海嶺のすぐ右側のプレートは消失し，全体が一つのプレートとなります．また， (f) では断層の長さがゼロになった後は (d) の鏡像の形となって断層は左ずれとなり，断層の長さの増大が始まります．

問題７−２−２ 解答

TTT(a)型： 通常は不安定なタイプですが，前問のように２つの海溝が直線をなすときと，この場合のようにプレート A に対するプレート C の速度ベクトル \({_A}{\bf V}{_C}\) が海溝 bc に平行な場合は安定となります．

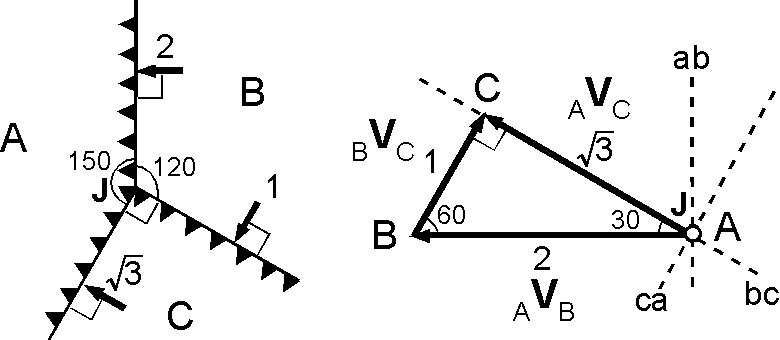
プレート C が海溝 bc に平行に移動しているTTT型３重会合点での速度空間表示

TTR(a)型： \({_A}{\bf V}{_C}\) と \({_B}{\bf V}{_C}\) が海嶺 ab に対して対称なために，３重会合点は安定となります．

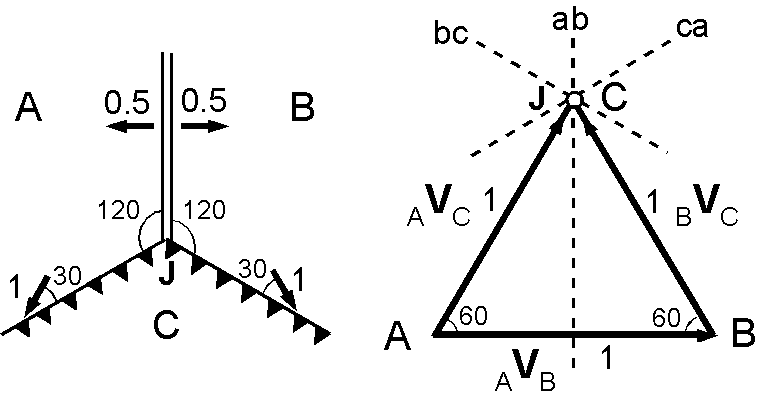
安定なTTR型３重会合点の例

TTF(b)型： \({_B}{\bf V}{_C}\) が海溝 ca に平行なため安定となります．

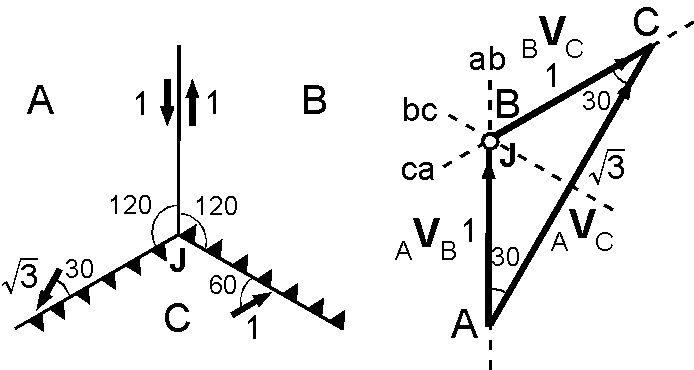
安定なTTF型３重会合点での速度空間表示

FFR型： \({_A}{\bf V}{_C}\) と \({_B}{\bf V}{_C}\) が海嶺 ab に対して対称なために，３重会合点は安定となります．

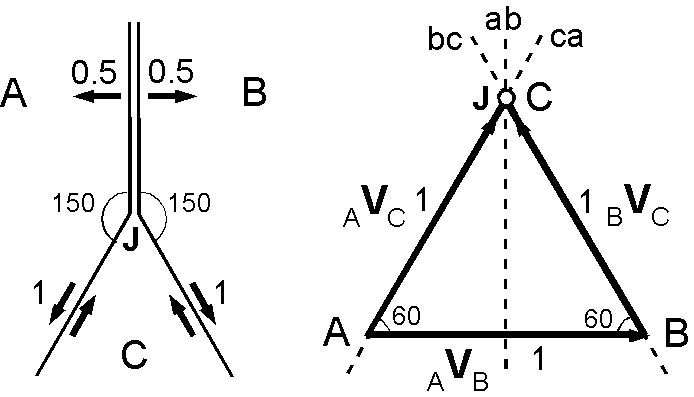
安定なFFR型３重会合点での速度空間表示

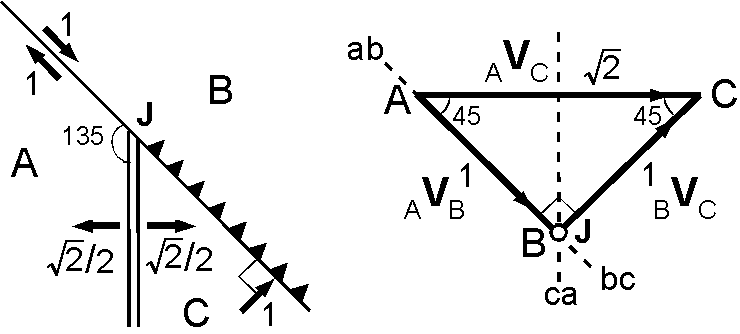
FFT 型： 海溝 ab とトランスフォーム断層 bc が直線をなすため３重会合点は安定となります．

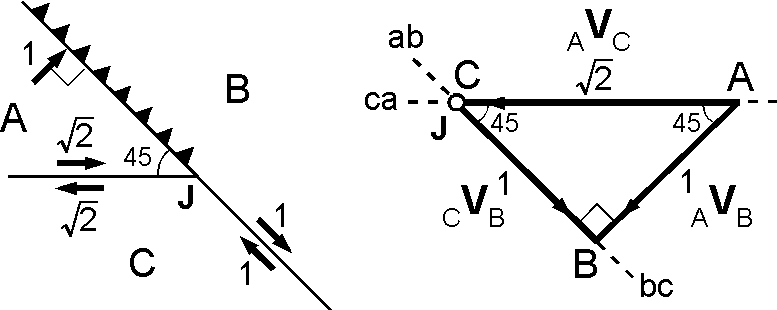
安定なFFT型３重会合点での速度空間表示

RTF(a)型： トランスフォーム断層 ab と海溝 bc が直線をなすため３重会合点は安定となります．

安定なRTF型３重会合点での速度空間表示

問題７−２−３ 解答

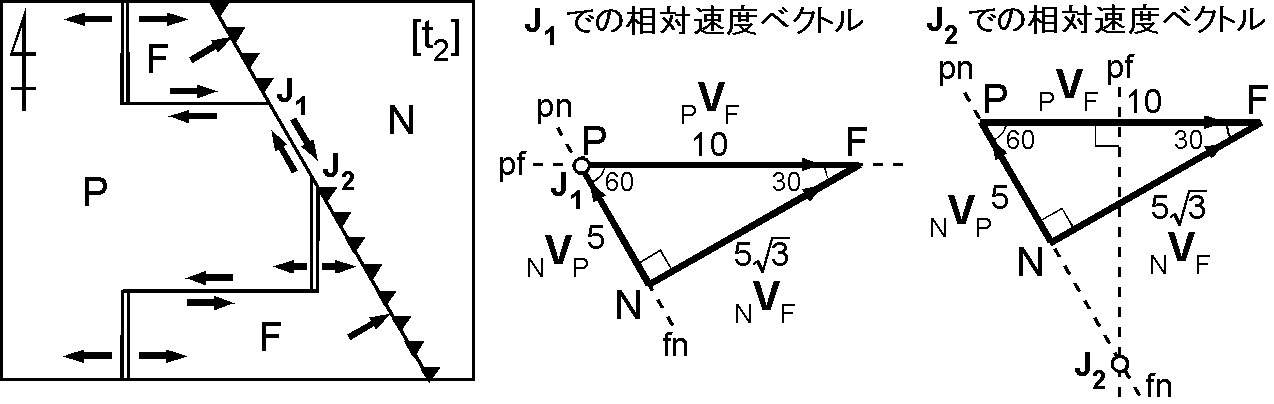
時代 t2： ３重会合点 J1 と J2 はそれぞれ前問の FFT 型と RTF 型に相当します．３つの相対速度ベクトルによる三角形は図のようになり， N に対する P の速度ベクトル \({_N}{\bf V}{_P}\) は西に 30° の方向で大きさは 5 cm/yr となります．この速度ベクトルは N の西の端に平行ですので，トランスフォーム断層が形成されます．３重会合点の移動方向などは図から次のようになります．

この時代にはサンアンドレアス断層は北米プレートから見ると，北の端は北上し南の端は南下して，その長さが増大し続けたことになります．

サンアンドレアス断層の時代t2における３重会合点での速度空間表示

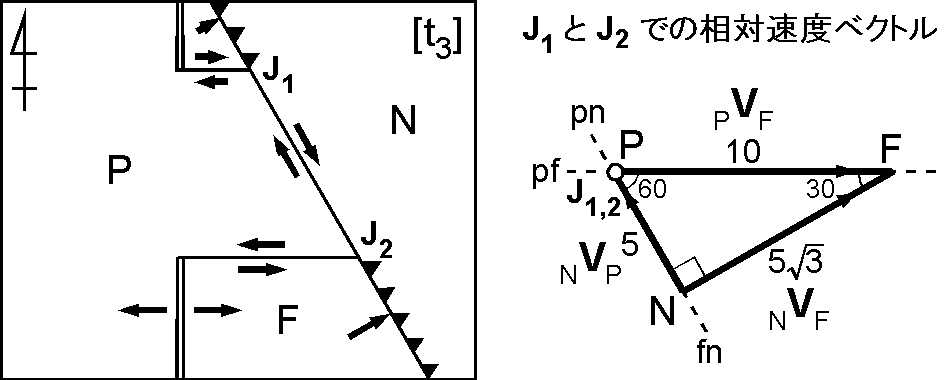
時代 t3： ２つの３重会合点における相対速度ベクトルの三角形は両者とも上の J1 と同じとなります．

この時代になると，サンアンドレアス断層は長さが一定のまま北米プレートの西端に沿って北へ移動を続けたことになります．

サンアンドレアス断層の時代t3における３重会合点での速度空間表示

→ ホーム