5-3 時間周期変動する地表温度の伝播 -- 非定常熱伝導方程式
1次元非定常熱伝導方程式: 前ページでは,微小距離 \(\delta x\) 離れた,2つの単位面積の平面で囲まれた空間から流出する熱が空間内の熱源により補充されるとして,熱伝導方程式を導きました.ここでは熱源はないとして,熱の流出は当該空間の温度低下で補充されます.単位時間に流出する熱エネルギーは熱伝導度を \(k\) として前ページの結果から, \[ -k\frac{\partial^2 T}{\partial x^2}\delta x, \] です (偏微分は変数が2つのため).一方,温度の低下で単位時間当たり発生する熱エネルギーは,密度と比熱を \(\rho\) と \(c\) とし,温度の時間微分が負であることを考慮して, \[ -\rho c \frac{\partial T}{\partial t}\delta x, \] となります.これらの2式を等置することで,次の1次元非定常熱伝導方程式を得ます. \begin{equation} \rho c \frac{\partial T}{\partial t} = k\frac{\partial^2 T}{\partial x^2}. \label{eq01} \end{equation} 通常は,熱拡散率とよばれる次のパラメーター, \begin{equation} \kappa = \frac{k}{\rho c}, \label{eq02} \end{equation} を導入して,1次元非定常熱伝導方程式は次式で表わされます. \begin{equation} \frac{\partial T}{\partial t} = \kappa \frac{\partial^2 T}{\partial x^2}. \label{eq03} \end{equation}
熱拡散の特徴的な距離スケールと時間スケール: 式 (2) の熱拡散率 \(\kappa\) は物質の熱伝導による熱の失われ易さを表わす量です.熱伝導度 \(k\),密度 \(\rho\),比熱 \(c\) の単位はそれぞれ W/m K, kg/m3, J/kg K ですので,熱拡散率の単位は, \[ \mathrm{ \left[\frac{W}{m\,K}\right]\cdot \left[\frac{kg}{m^3}\right]^{-1}\cdot\left[\frac{J}{kg\,K}\right]^{-1} = \left[\frac{J}{s\,m\,K}\frac{m^3}{kg}\frac{kg\,K}{J}\right] = \left[\frac{m^2}{s}\right] }, \] のように,距離の2乗を時間で割った形となります.そこで,熱拡散率が \(\kappa\) の物質中を熱が距離 \(\ell\) 伝わるのに要する時間 \(\tau\) の大まかな見積もりは次元解析により, \begin{equation} \tau =\ell^2/\kappa, \label{eq04} \end{equation} となり,これを熱拡散の特徴的時間スケールといいます.逆に,時間 \(\tau\) の間に熱が到達する特徴的距離スケールは次の式で得られます. \begin{equation} \ell = \sqrt{\kappa\tau}. \label{eq05} \end{equation} ここで典型的な熱拡散率の値として, \(k\) = 3.3 W/m K, \(\rho\) = 3300 kg/m3, \(c\) = 1000 J/kg とすると, \(\kappa\) = 1×10-6 m2/s を使用することにします.例として地球が熱伝導で冷却するに要する特徴的時間スケールを,特徴的距離を地球半径の 6400 km として計算してみると, \[ \tau = (6.4\times 10^6)^2\div 10^{-6}\div(365\times 24\times 3600) = 1.3\times 10^{12}\ \mathrm{yr}. \] この 1.3 兆年という非現実的な値は,地球などの天体の冷却は主に熱輸送効率の高い熱対流によることを示唆します.しかし,熱伝導だけによる現象については下記の問題5-3-1のように,式 (4) や (5) から特徴的距離や時間を正しく見積もることができます.
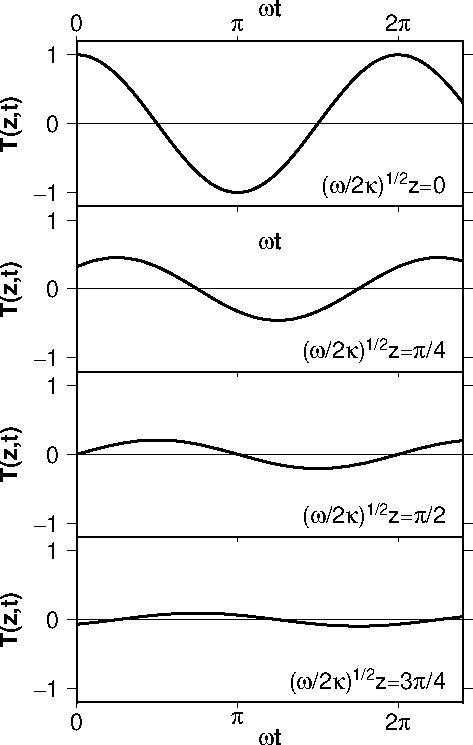
時間周期変動する地表温度の伝播: 地表温度が日変化や季節変化をするとき,地下温度の変化は地表ほど大きくないことはよく知られています.このような問題を1次元非定常熱伝導方程式を用いて解いた結果を右図に示します (パラメーターの詳細は後述).最上段は地表温度の変動で,下段は深さとともに変動の振幅が減少し,変動の位相も遅れることを示します.以下は Fowler (2005) に従った解析の詳細です.
地表温度が次式のように平均値のまわりに振幅 \(T_0\) で時間 \(t\) の余弦関数で変動しているとします. \begin{equation} T = T_0\cos\omega t. \label{eq06} \end{equation} 但し, \(\omega\) は角周波数で,周期は \(2\pi/\omega\) です.地表を原点とし,深さ方向に \(z\) 軸を取ると,地下の温度変動 \(T(z,t)\) は次の熱伝導方程式を解くことで得られます. \begin{equation} \frac{\partial T}{\partial t} = \kappa \frac{\partial^2 T}{\partial z^2}. \label{eq07} \end{equation} \(z\) = 0 での境界条件が式 (6) ですが,ここでは三角関数の指数関数表示, \(e^{i\theta} = \cos\theta + i\sin\theta\) (\(i=\sqrt{-1}\)),を使用します.複素関数は専門レベルの数学ですが,ここでは式の変形が楽になるので使用し,結果は単に実数部を採用すると簡単に考えます.従って, \(z\) = 0 と \(z\) = \(\infty\) での境界条件は次のようになります. \begin{eqnarray} T(0,t) & = & T_0e^{i\omega t}, \label{eq08} \\ T(\infty,t) & = & 0. \label{eq9} \end{eqnarray} 式 (7) の解法の1つとして, \(T(z,t)\) を \(z\) の関数 \(X(z)\) と \(t\) の関数 \(Y(t)\) との積で表わします. \begin{equation} T(z,t) = X(z)Y(t). \label{eq10} \end{equation} (10) を (7) へ代入して, \[ \frac{1}{Y}\frac{dY}{dt} = \kappa\frac{1}{X}\frac{d^2X}{dz^2}, \] となりますが, \(t\) だけの左辺と \(z\) だけの右辺が常に等しいので,この等式は定数である必要があります.定数を \(c\) として次の2つの微分方程式を得ます. \begin{eqnarray} \frac{dY}{dt} & = & cY, \label{eq11} \\ \frac{d^2X}{dz^2} & = & \frac{c}{\kappa}X. \label{eq12} \end{eqnarray} (11) の解は, \(a\) を定数として, \[ Y = ae^{ct}, \] ですが,境界条件 (8) と比較すると \(c=i\omega\) となり,次の \(Y\) を得ます. \begin{equation} Y = ae^{i\omega t}. \label{eq13} \end{equation} (12) の解は, \(c=i\omega\) ですので \(b_1\) と \(b_2\) を定数として, \[ X = b_1e^{-z\sqrt{i\omega/\kappa}} + b_2e^{z\sqrt{i\omega/\kappa}}, \] ですが, \(\sqrt{i} = (1+i)/\sqrt{2}\) の関係を利用して, \[ X = b_1e^{-(1+i)z\sqrt{\omega/2\kappa}} + b_2e^{(1+i)z\sqrt{\omega/2\kappa}}, \] となります.これを境界条件 (9) と比較すると \(b_2\) = 0 となり, \(X\) は次式となります. \begin{equation} X = b_1e^{-(1+i)z\sqrt{\omega/2\kappa}}. \label{eq14} \end{equation} (13) と (14) を (10) に代入して, \begin{eqnarray*} T(z,t) & = & ae^{i\omega t}b_1e^{-(1+i)z\sqrt{\omega/2\kappa}}, \\ & = & ab_1e^{-z\sqrt{\omega/2\kappa}}e^{i(\omega t-z\sqrt{\omega/2\kappa})}. \end{eqnarray*} となり,式 (8) から \(ab_1=T_0\) となり,実数部を取ることで次の地下温度変動を得ます. \begin{equation} T(z,t) = T_0e^{-z\sqrt{\omega/2\kappa}}\cos\left(\omega t-z\sqrt{\omega/2\kappa}\right). \label{eq15} \end{equation} 式 (15) の結果は地下温度の変動の振幅は深さの指数関数で減少し, \(\omega\) が大きいほど,即ち周期が短いほど速く減少することを示しています.振幅が \(1/e\) に減少する深さをスキンデプス(skin depth,表皮深さ)といい, \(d_\omega\) で表わすと, \begin{equation} d_\omega = \sqrt{\frac{2\kappa}{\omega}}. \label{eq16} \end{equation} となります.一方,地下温度の変動の周期は地表と同じですが時間の遅れがあることも式 (15) から分かります.上で示したグラフは \(z\sqrt{\omega/2\kappa}\) が \(\pi\)/4 ずつ増すときの様子を示しています.
問題5-3-1
地表の温度変化が, (a) 1日周期, (b) 1年周期, (c) 1万年周期の3つの場合について,スキンデプス(\(d_\omega\)),熱拡散の特徴的距離スケール(\(\ell\)),振幅が 1/10 に減少する深さ(\(d_1\)),位相が 180 度遅れる深さ(\(d_2\))を計算しなさい.地下の熱拡散率 \(\kappa\) は 1×10-6 m2/s とします.
問題5-3-2
地表温度の時間周期変動に起因する地表面の熱流を考えます.ここでは,本文の理論と同様,地球深部からの恒常的な熱流は考慮しません (正確には,地表温度変動による熱流が恒常的熱流に加わる).さて,地表面の熱流は地表温度が平均値より高い時期は下向きで,低い時期は上向きになると予想されます.しかし,実際には地表の熱流は地表の温度変動に先行します.
(1) 地下の熱伝導度を \(k\) として本文の式 (15) から \(-k\left[\frac{dT}{dz}\right]_{z=0}\) を計算することで,地表での熱流量 \(q_0\) が次式で表わされることを導きなさい. \[ q_0 = kT_0\sqrt{\frac{\omega}{\kappa}}\cos\left(\omega t + \frac{\pi}{4}\right). \]
(2) 上の式から,地表の熱流量がゼロとなるときの \(\omega t\) を求めなさい.
参考文献:
- Fowler, C.M.R., The Solid Earth: An Introduction to Global Geophysics, 685 pp., Cambridge University Press, 2005.