問題5−3−1 解答
- 角周波数 \(\omega\) は 2π を秒単位の周期で割って求めます.
- スキンデプス \(d_\omega\) は本文の式 (16) を計算します. \[ d_\omega = \sqrt{2\kappa/\omega}. \]
- 熱拡散の特徴的距離スケール \(\ell\) は本文の式 (5) で \(\tau\) に周期を代入します. \begin{eqnarray*} \ell & = & \sqrt{\kappa\tau} = \sqrt{\kappa(2\pi/\omega)}, \\ & = & \sqrt{\pi}d_\omega. \end{eqnarray*}
- 振幅が 1/10 に減少する深さ \(d_1\) は本文の式 (15) の振幅の項から計算します. \begin{eqnarray*} e^{-d_1\sqrt{\omega/2\kappa}} & = & 0.1, \\ d_1 & = & -\log_e(0.1)\sqrt{2\kappa/\omega}, \\ & = & 2.30 d_\omega. \end{eqnarray*}
- 位相が 180 度遅れる深さ \(d_2\) は本文の式 (15) の位相を表わす項から計算します. \begin{eqnarray*} d_2\sqrt{\omega/2\kappa} & = & \pi, \\ d_2 & = & \pi\sqrt{2\kappa/\omega}, \\ & = & \pi d_\omega. \end{eqnarray*}
これらの手順に従い, \(\kappa\) = 1×10-6 m2/s として計算した結果は次表の通りです.
| 周期 | \(\omega\) [1/s] | \(d_\omega\) [m] | \(\ell\) [m] | \(d_1\) [m] | \(d_2\) [m] |
| 1日 | 7.272×10-5 | 0.166 | 0.294 | 0.382 | 0.521 |
| 1年 | 1.992×10-7 | 3.17 | 5.62 | 7.30 | 9.95 |
| 1万年 | 1.992×10-11 | 317 | 562 | 730 | 995 |
1日周期の結果からは,地表温度の日変化の地下への影響はせいぜい数十センチであることが分かります.1年周期の結果では,位相が 180° 遅れる深さが約 10 m です.このことから,深さ 10 m 付近の地下水は夏は冷たく,冬は温かいことが考えられます.周期1万年の結果からは,氷期-間氷期などの気候変動の影響を受けない地殻熱流量や地下温度の測定には,随分と深い観測井戸を掘削する必要があることが分かります.深さ 730 m でも地表温度の変動幅の影響が 10% 残っていることになります.
問題5−3−2 解答
(1) 本文で得た結果より深さ \(z\),時間 \(t\) での温度は, \begin{equation} T(z,t) = T_0e^{-z\sqrt{\omega/2\kappa}}\cos\left(\omega t-z\sqrt{\omega/2\kappa}\right). \label{eq01} \end{equation} これを \(z\) で微分すると, \begin{eqnarray} \frac{dT}{dz} & = & \small{ -T_0\sqrt{\frac{\omega}{2\kappa}}e^{-z\sqrt{\frac{\omega}{2\kappa}}}\cos\left(\omega t - z\sqrt{\frac{\omega}{2\kappa}}\right) + T_0\sqrt{\frac{\omega}{2\kappa}}e^{-z\sqrt{\frac{\omega}{2\kappa}}}\sin\left(\omega t - z\sqrt{\frac{\omega}{2\kappa}}\right) }, \nonumber \\ & = & -T_0\sqrt{\frac{\omega}{2\kappa}}e^{-z\sqrt{\frac{\omega}{2\kappa}}}\left[\cos\left(\omega t - z\sqrt{\frac{\omega}{2\kappa}}\right) - \sin\left(\omega t - z\sqrt{\frac{\omega}{2\kappa}}\right)\right]. \label{eq02} \end{eqnarray} これを次の公式を用いて変形します. \begin{eqnarray*} & & a\cos\theta - b\sin\theta=\sqrt{a^2+b^2}\cos(\theta+\alpha), \\ \mathrm{where}, & & \quad \cos\alpha=\frac{a}{\sqrt{a^2+b^2}}, \quad \sin\alpha=\frac{b}{\sqrt{a^2+b^2}}. \end{eqnarray*} 式 (2) では, \(a\) = \(b\) = 1 より \(\alpha\) = π/4 で, \(\sqrt{a^2+b^2}\) = \(\sqrt{2}\) を考慮して熱流は次式となります. \begin{equation} q(z,t) = -k\frac{dT}{dz} = kT_0\sqrt{\frac{\omega}{\kappa}}e^{-z\sqrt{\frac{\omega}{2\kappa}}}\cos\left(\omega t - z\sqrt{\frac{\omega}{2\kappa}} + \frac{\pi}{4}\right). \label{eq03} \end{equation} この式は地下の熱流も地下温度と同様に深さとともに減少し,同じ周期で変動することを示しますが,変動の位相が 45° 進んでいることが分かります.地表での熱流量 \(q_0\) は \(z\) = 0 とおいて, \begin{equation} q_0 = kT_0\sqrt{\frac{\omega}{\kappa}}\cos\left(\omega t + \frac{\pi}{4}\right). \label{eq04} \end{equation}
(2) 式 (4) で, \(\cos(\omega t + \pi/4)\) がゼロとなる条件は \(n\) を整数として, \[ \omega t + \frac{\pi}{4} = \frac{\pi}{2} + n\pi, \] より, \begin{equation} \omega t = \frac{\pi}{4} + n\pi, \quad n=1,2,3,\cdots \label{eq05} \end{equation}
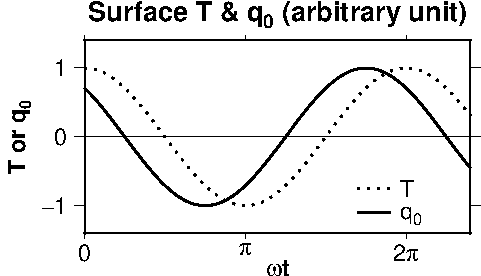
図は地表温度の変動(点線)に対する地表熱流量の変動(実線)を,両者とも縦軸を1として示します.熱流の変化が温度の変化に先行することは不思議に感じます.しかし,例えば温度の極大が時間遅れで地下に伝わって行く場合を想定すると,温度がゼロになる前に温度勾配が逆転することが考えられます.
なお,地表の温度変化による熱流は地球深部からの恒常的な熱流に比べて圧倒的に大きいです.\(T_0\) = 10 °C, \(k\) = 3 W/m K, \(\kappa\) = 10-6 m2/s として,
- 日変化では, \[ 3\times10\times\sqrt{7.2722\times 10^{-5}\div 10^{-6}} = 255\ \mathrm{W/m^2}. \]
- 年変化では, \[ 3\times10\times\sqrt{1.9924\times 10^{-7}\div 10^{-6}} = 13.4\ \mathrm{W/m^2}. \]
となり,年変化でさえ大陸における平均の地殻熱流量 65 mW/m2 の2百倍の大きさです.