3-4 自転とコリオリ力
フーコーの振り子: 地球の自転の証拠として,振り子の振動面が地面に対して回転することが 19 世紀にフーコーにより示されました.振子の振動面が回転する原理は北極や南極では容易に理解できます.それは,北極と南極では地面が鉛直線のまわりに1日で 360°,それぞれ反時計と時計方向に回転し,静止系に固定された振動面はその逆方向へ同じ角速度で回転するように見えるからです.しかし,極以外の地点では地面が鉛直線のまわりにどのように回転するかは自明ではありません.
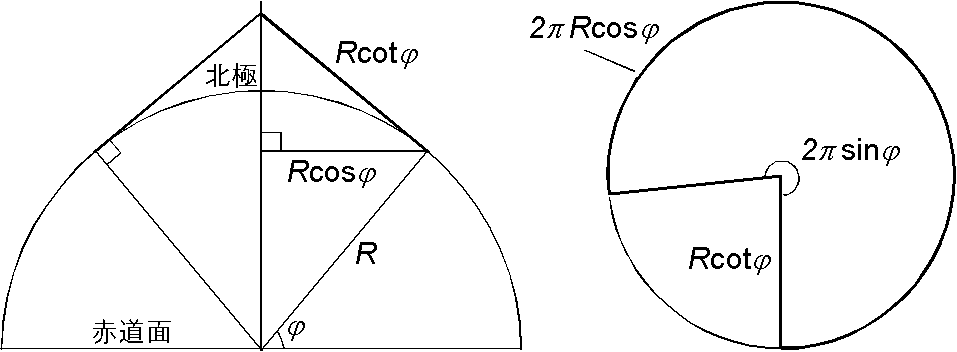
一般的な説明は,ある緯度線で地球に接する円錐を考え,その円錐を平面に展開すると,扇型の弧に対する中心角がその緯度の地面が1日で回転した角度になることです.よって図から,緯度 \(\varphi\) の地面の角速度 \(\omega^\prime\) と地球の自転の角速度 \(\omega\) の比は,弧の長さと円の全周との比ですので, \[ \omega^\prime = \omega\times(2\pi R\cos\varphi\div 2\pi R\cot\varphi) = \omega\sin\varphi. \] よって,振動面の回転速度は緯度が低いほど遅くなり,赤道では回転しないことになります.
角速度ベクトル: 物理学では回転の角速度をベクトルとして定義します.角速度ベクトル \(\boldsymbol{\omega}\) は大きさが \(\omega\) で,向きが右ねじの回転で進む方向に取ったベクトルです.1つの角速度ベクトルを成分に分解したり,幾つかの角速度ベクトルを合成することもでき,回転運動の記述に便利です.ここでは,地面の鉛直線のまわりの回転を角速度ベクトルを使用して考えます.
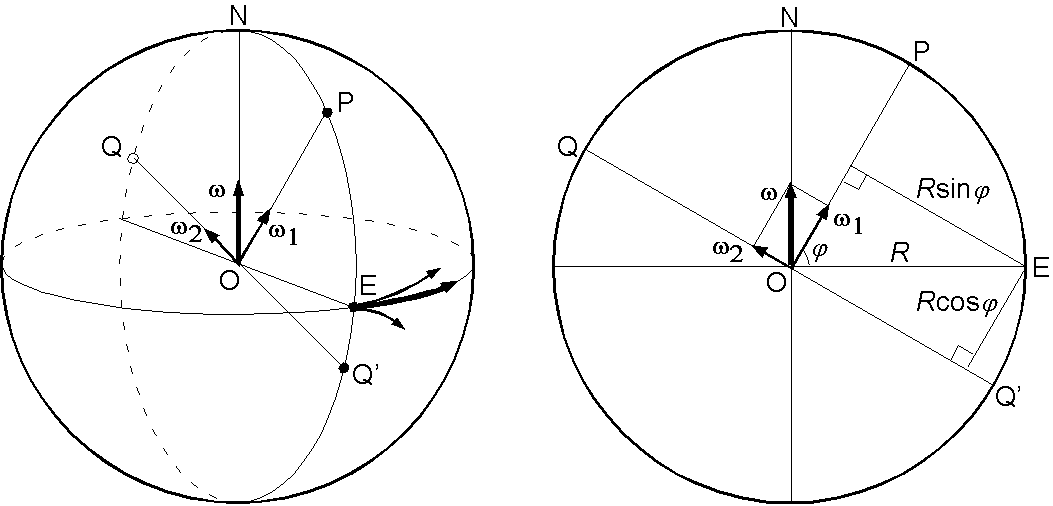
地球の自転の角速度ベクトル \(\boldsymbol{\omega}\) を,緯度 \(\varphi\) の地点 P の方向の成分 \(\boldsymbol{\omega}_1\) とそれに直角な成分 \(\boldsymbol{\omega}_2\) に分解します.すると,地点 P における水平面(地面)の回転の大きさは \(\omega_1\) で与えられるので,その大きさは図から, \[ \omega_1 = \omega\sin\varphi, \] となり,円錐による方法と同じ結果が得られました.
このように角速度ベクトルは分解や合成が可能であることは,無限小回転がベクトルとして扱えることから導かれます(→ 解説はここにあります).しかしこのページでは,直感的説明として赤道上の地点 E の動く方向と速度について図から考えます.左図で点 E はベクトル \(\boldsymbol{\omega}\) から地球半径 \(R\) の距離にありますので,その運動方向は太い矢印で示したように赤道に沿って東向きで,速度は \[ \omega R, \] です.一方,角速度ベクトルを \(\boldsymbol{\omega}_1\) と \(\boldsymbol{\omega}_2\) に分けた場合は,図の2つの細い矢印線で示した運動が重なります.点 E の \(\boldsymbol{\omega}_1\) による運動は P を中心とし E に接する小円で示され反時計回りです.点 E の \(\boldsymbol{\omega}_2\) による運動は Q' を中心とする小円で示され時計回りです.それらの速度の向きは赤道との接線ですのでいづれも赤道に沿って東向きです.右図から,点 E から \(\boldsymbol{\omega}_1\) と \(\boldsymbol{\omega}_2\) へ下ろした垂線の距離はそれぞれ, \(R\sin\varphi\) と \(R\cos\varphi\) ですので,合成した速度は東向きに, \[ \omega_1 R\sin\varphi + \omega_2 R\cos\varphi = \omega R \sin^2\varphi + \omega R \cos^2\varphi = \omega R, \] となり,自転の角速度ベクトル \(\boldsymbol{\omega}\) による回転速度と同じ結果となります.
北極点 N の速度がゼロであることも同様にして示されます.点 N の \(\boldsymbol{\omega}_1\) による P の回りの回転速度は,右図で紙面上向きを正として, \[ \omega_1 R\cos\varphi = \omega R\sin\varphi\cos\varphi, \] で, \(\boldsymbol{\omega}_2\) による Q の回りの回転速度は紙面に下向きで, \[ -\omega_2 R\sin\varphi = -\omega R\cos\varphi\sin\varphi, \] ですので,両者を加えるとゼロとなることが示されました.
回転座標系での見掛けの力: 静止座標系で,位置ベクトル \({\bf r}\) に位置する質量 \(m\) の質点に力 \({\bf F}\) が作用すると質点は次のニュートンの運動方程式に従って加速度を得ます. \begin{equation} m\frac{d^2}{dt^2}{\bf r} = {\bf F}. \label{eq01} \end{equation} この現象を一定の角速度 \(\boldsymbol{\omega}\) で回転する回転座標系で見ると,見掛けの力が加わった運動方程式となります.その導出を木村 (1983) に従い,以下にまとめます.
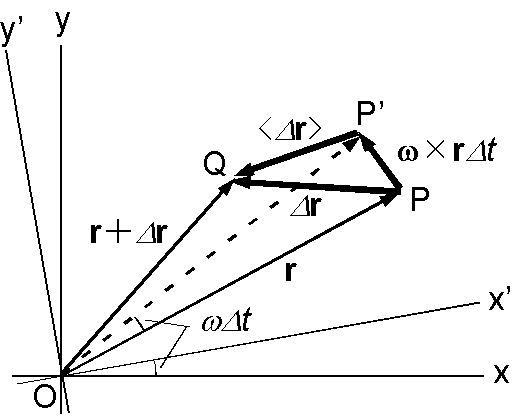
静止座標系 x-y-z の x-y 平面上の点 P (\({\bf r}\)) にある質点が微小時間 \(\Delta t\) の間に微小距離 \(\Delta {\bf r}\) 離れた点 Q (\({\bf r}+\Delta {\bf r}\)) へ移動したとします.これを原点 O のまわりに角速度 \(\omega\) で回転する回転座標系 x'-y' からはどう見えるかを考えます.いま,点 P が \(\Delta t\) の間に O の回りに角度 \(\omega\Delta t\) 回転した点を P' とします.すると,質点は回転座標系では P' から Q へ移動したように見えるはずです.この微小の距離を \(\langle\Delta {\bf r} \rangle\) で表します.ここに,\(\langle \rangle\) は回転座標系で定義される量を表します.距離 PP' は \(\omega\Delta t r\) ですが,角速度ベクトル \(\boldsymbol{\omega}\) = (0, 0, \(\omega\)) を用いると,ベクトル積 \(\boldsymbol{\omega}\times{\bf r}\Delta t\) で表せますので,次の関係式が得られます. \[ \Delta {\bf r} = \langle\Delta{\bf r}\rangle + \boldsymbol{\omega}\times{\bf r}\Delta t. \] さらに, \(\Delta t \rightarrow 0\) として微分で表すと次式となります. \begin{equation} \frac{d}{dt}{\bf r} = \left\langle\frac{d}{dt}\right\rangle{\bf r} + \boldsymbol{\omega}\times{\bf r}. \label{eq02} \end{equation} 実は, (2) に含まれる次の関係式は静止系と回転系との間の時間微分の変換を表す演算子であり,任意のベクトルに適用できることが示されています. \begin{equation} \frac{d}{dt} = \left\langle\frac{d}{dt}\right\rangle + \boldsymbol{\omega} \times. \label{eq03} \end{equation} そこで,この演算子を (2) の \(\frac{d}{dt}{\bf r}\) 自身に適用して, \begin{eqnarray} \frac{d}{dt}\frac{d}{dt}{\bf r} & = & \left\langle\frac{d}{dt}\right\rangle\frac{d}{dt}{\bf r} + \boldsymbol{\omega}\times\frac{d}{dt}{\bf r}, \nonumber \\ & = & \left\langle\frac{d}{dt}\right\rangle\left(\left\langle\frac{d}{dt}\right\rangle{\bf r} + \boldsymbol{\omega}\times{\bf r}\right) + \boldsymbol{\omega}\times\left(\left\langle\frac{d}{dt}\right\rangle{\bf r} + \boldsymbol{\omega}\times{\bf r}\right), \nonumber \\ & = & \left\langle\frac{d^2}{dt^2}\right\rangle{\bf r} + 2\boldsymbol{\omega}\times\left\langle\frac{d}{dt}\right\rangle{\bf r} + \boldsymbol{\omega}\times\boldsymbol{\omega}\times{\bf r}. \label{eq04} \end{eqnarray} この式の両辺に質点の質量 \(m\) を掛けて (1) を代入すると, \[ {\bf F} = m\left\langle\frac{d^2}{dt^2}\right\rangle{\bf r} + 2m\boldsymbol{\omega}\times\left\langle\frac{d}{dt}\right\rangle{\bf r} + m\boldsymbol{\omega}\times\boldsymbol{\omega}\times{\bf r}, \] となりますが,回転座標系における加速度の項を左辺に移行して整理すると, \[ m\left\langle\frac{d^2}{dt^2}\right\rangle{\bf r} = {\bf F} - 2m\boldsymbol{\omega}\times\left\langle\frac{d}{dt}\right\rangle{\bf r} - m\boldsymbol{\omega}\times\boldsymbol{\omega}\times{\bf r}, \] となりますが,今後は回転座標系だけで考えることにすれば,記号 \(\langle \rangle\) は取り去り,速度 \({\bf v}\) と加速度 \({\bf a}\) の表記を使用して,回転座標系における次の運動方程式を得ます. \begin{equation} m{\bf a} = {\bf F} - 2m\boldsymbol{\omega}\times{\bf v} - m\boldsymbol{\omega}\times\boldsymbol{\omega}\times{\bf r}. \label{eq05} \end{equation} この式の導出には2次元の平面を仮定したのですが,地球の自転のような3次元の場合にも成立することが示されています. (5) の右辺の第2項と第3項はそれぞれコリオリ力(転向力)と遠心力です.これらの力は見掛けの力(慣性力)と呼ばれますが,回転座標系上の観測者には実際に働く力です.第3項の遠心力が回転中心からの距離に依存するのに対して,第2項のコリオリ力は速度に依存します.そのため,コリオリ力は同じ速度ベクトルであれば回転中心からの距離に関わらず同じ力として働きます.
ここで注意すべき点としては,地球上で運動する物体に働くコリオリ力は,次の問題3-4-1でみるように,通常は水平方向に働く力と鉛直方向に働く力からなることです.コリオリ力の水平成分はフーコーの振り子の原因ですが,鉛直成分は → 問題3-2-2で考察したエトベス効果の原因です.
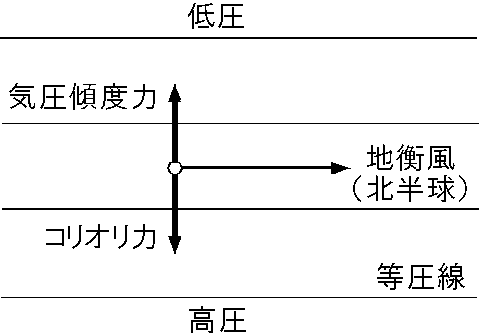
しかし,コリオリ力の鉛直成分はその方向に働く重力に比べて大変小さいため,気象や海洋の分野では通常は水平成分だけに着目します.そのため,一般にコリオリ力は北半球では運動方向に直角右向きに,南半球では直角左向きに働くと表現されます.コリオリ力の水平成分はフーコーの振り子だけでなく,大気や海洋の流れにも大きく影響します.右図は北半球における地衡風の発生の説明図です.空気塊は気圧傾度力の方向へ動き出しますが,速度の上昇に応じてコリオリ力も増大し空気塊の動きは右方向へそれます.地表からの摩擦力のない上空では,気圧傾度力とコリオリ力が釣り合う安定状態に達し,風向きは等圧線に平行になります.
問題3-4-1
北半球で働くコリオリ力についての次の問いに答えなさい.
- (1)東向きに時速 100 km で走る車内にいる重さ 50 kg の人に働くコリオリ力の大きさと方向を求めなさい.
- (2)問い(1)で緯度を 30°N とするとき,コリオリ力の水平成分の大きさと方向を求めなさい.
問題3-4-2
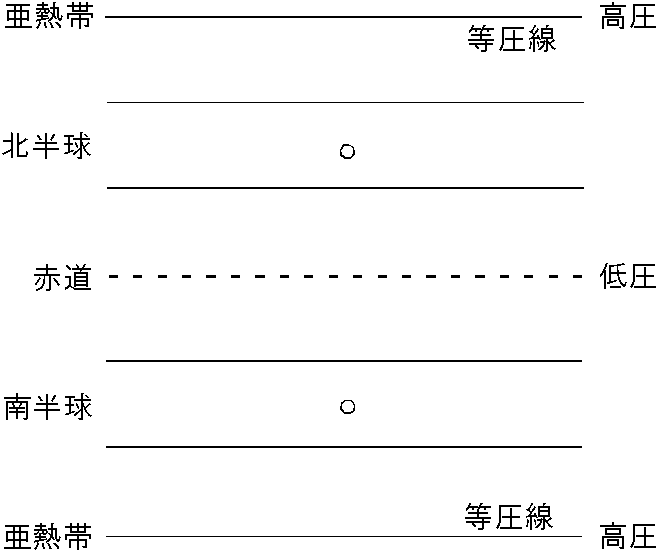
亜熱帯の高圧帯から赤道に向けて海面近くを吹く貿易風のモデルを考えます.海面からの摩擦力が気圧傾度力の 1/2 になった時点で,気圧傾度力,摩擦力,コリオリ力(水平成分)の3つの力が釣り合い,安定状態に達したと仮定します.図の白丸で示した空気塊に働く力の釣り合いを風の向きとともに図示しなさい.
参考文献:
- 木村竜治, 地球流体力学入門ー大気と海洋の流れのしくみー, 247 pp., 東京堂出版, 1983.