その他:主磁場成分の計算
その他:主磁場成分の計算
プログラム "igrf" はある地点で観測される地磁気主磁場の成分を計算します.日時は AD 1900--2029 の間で指定します.地点の緯度経度は WGS84 測地座標系と地心座標系の何れかを指定でき,また地点の標高や地球中心からの半径を指定できます.ガウス係数は IGRF-14(→ IGRF maintained by IAGA, 2025)を使用し,ガウス係数は AD 2000 以降は n=13 まで,AD 2000 より前は n=10 まで含めています.
地点・日時を入力しての計算
オプションを指定しない場合,観測点の緯度と経度は地理(測地)座標系で,日時も含めて十進法で入力します.以下は "igrf" とタイプし,続いて "Return" とした場合の計算例です.
igrf Main field from IGRF-14 with n=13 (yr>=2000) or n=10 (yr<2000) Rtn (Enter) to continue, U for usage, H for help message, Q to quit. ** Geodetic system adopted. ** Decimal year? (Q - quit) 2024.3 Altitude in km? (-10 ~ 500 km) (Rtn - 0 km, Q - quit) 0.2 Decimal Lat, Lon? (Q - quit) 64.7 -26.4 Year altitude 2024.300 0.2 Latitude Longitude 64.70 -26.40 X Y Z F I D 12402 -3171 51341 52913 76.00 -14.34 Decimal Lat, Lon? (Q - quit)
オプション -C では計算は地心座標系で行われ,地球中心からの半径を指定します.「年,月,日」と「度,分」による入力はそれぞれ,オプション -Y と -D で可能です.
データファイルからの入力
オプション -F を使用すると, "igrf" は地点と日時のデータをファイルから読み込み,計算結果をディスプレイに出力します.データの形式は「十進」,「年,月,日」,「度,分」いづれも可能ですが,座標系は測地系のみで,次の例のようになります.
igrf -f t-igrf.d > result.txt
以下は, "result.txt" に出力された計算結果です.
** IGRF elements from t-igrf.d **
** Geodetic system adopted. **
Year Mo Dy altitude
2025 5 15 0.2
Lat-d Lat-m Lon-d Lon-m
33 24 -133 36
X Y Z F I D
24004 5468 35179 42938 55.02 12.83
...
... 以下,省略 ...
...
プログラムのダウンロードとインストーレーション
公式の概要
観測点 (\(r,\theta,\phi\)) における地磁気ベクトル \({\bf B}\) の北,東,鉛直下向き成分をそれぞれ \(X\), \(Y\), \(Z\) とします.これらの3成分は,ガウス係数 \(g_n^m\) と \(h_n^m\) を用いて次の公式で与えられます.ここに, \(P_n^m(\cos\theta)\) は擬正規化されたシュミット球関数(ルジャンドル陪関数)です. \begin{eqnarray*} X & = & \sum_{n=1}^\infty\left(\frac{a}{r}\right)^{n+2}\sum_{m=0}^n(g_n^m\cos m\phi + h_n^m\sin m\phi)\frac{dP_n^m(\cos\theta)}{d\theta}, \\ Y & = & \sum_{n=1}^\infty\left(\frac{a}{r}\right)^{n+2}\sum_{m=0}^n(g_n^m\sin m\phi - h_n^m\cos m\phi)\frac{m P_n^m(\cos\theta)}{\sin\theta}, \\ Z & = & -\sum_{n=1}^\infty(n+1)\left(\frac{a}{r}\right)^{n+2}\sum_{m=0}^n(g_n^m\cos m\phi + h_n^m\sin m\phi)P_n^m(\cos\theta). \end{eqnarray*}
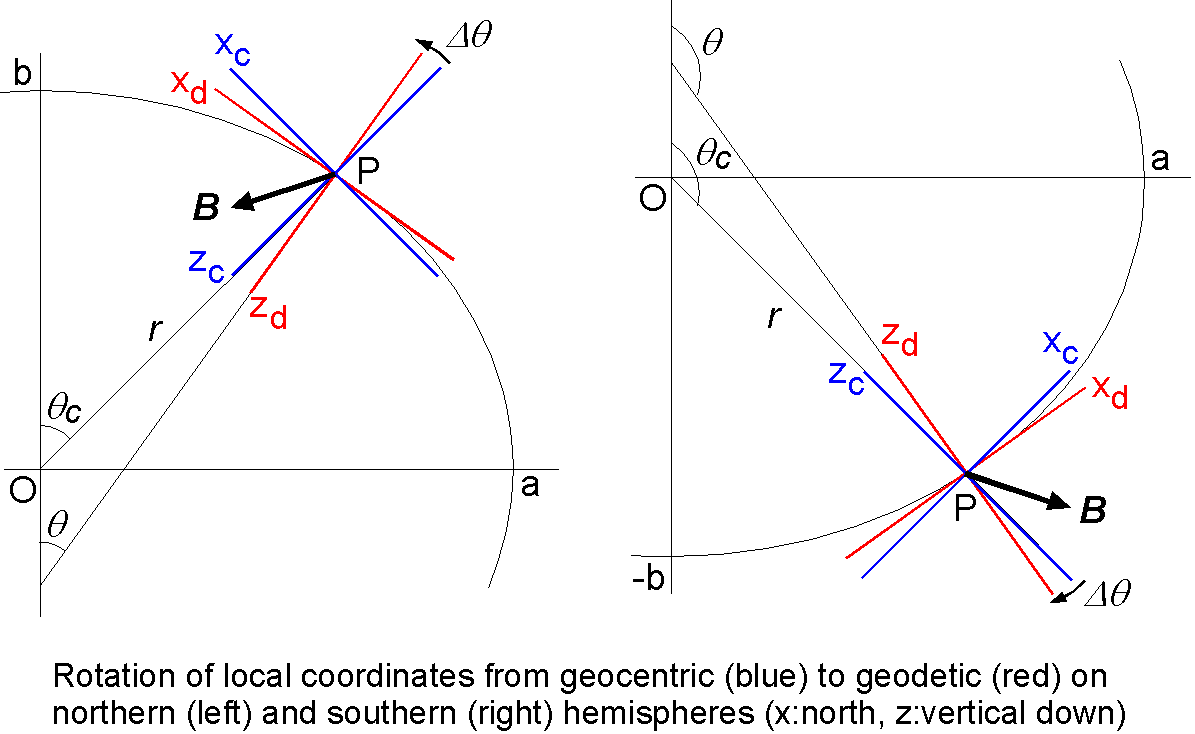
上の公式は地心座標系のみで成立しますが,地図やナビゲーションでは地理(測地)座標系が使用されています.そこで,最初に測地学による変換公式を使用して,測地座標系の余緯度 \(\theta\) を地心座標系の余緯度 \(\theta_c\) に変換し,地球中心からの半径 \(r\) を求めます(詳細は, "pmagt402.tar.gz" に含まれる "MEMOS_pmagt402.pdf" にあります).次に,地心座標系での磁場成分 (\(X_c,Y_c,Z_c\)) を上の公式を用いて計算します.最後に,これらの地心座標系の磁場成分を次の式を用いて,測地座標系における磁場成分 (\(X,Y,Z\)) へと変換します.ここに, \(\Delta\theta\) は観測点 P における2つの局地座標系の正負を考慮した角度差です. \[ \left(\begin{array}{c} X \\ Y \\ Z \end{array}\right) = \left(\begin{array}{ccc} \cos\Delta\theta & 0 & \sin\Delta\theta \\ 0 & 1 & 0 \\ -\sin\Delta\theta & 0 & \cos\Delta\theta \end{array}\right) \left(\begin{array}{c} X_c \\ Y_c \\ Z_c \end{array}\right) \]
下図に観測点 P における磁場ベクトル \({\bf B}\) と局地座標系の回転との関係を北半球(左図)と南半球(右図)について示しました.