6-2 地磁気ポテンシャル
ポテンシャルの概念については,「→ 3-5 重力ポテンシャルとジオイド」で扱いましたが,静磁場についても定義できます.一般に,電流の存在を無視できる静磁場 \({\bf B}\) はスカラーポテンシャル \(W\) により, \begin{equation} {\bf B} = -\nabla W, \label{eq01} \end{equation} で与えられます.ここに, \(\nabla\) (ナブラ) は次式で表わされる微分演算子です. \[ \nabla = \left(\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}\right). \] 式 (1) より磁場の各成分は次式で与えられます. \[ {\bf B} = \left(-\frac{\partial W}{\partial x}, -\frac{\partial W}{\partial y}, -\frac{\partial W}{\partial z}\right). \]
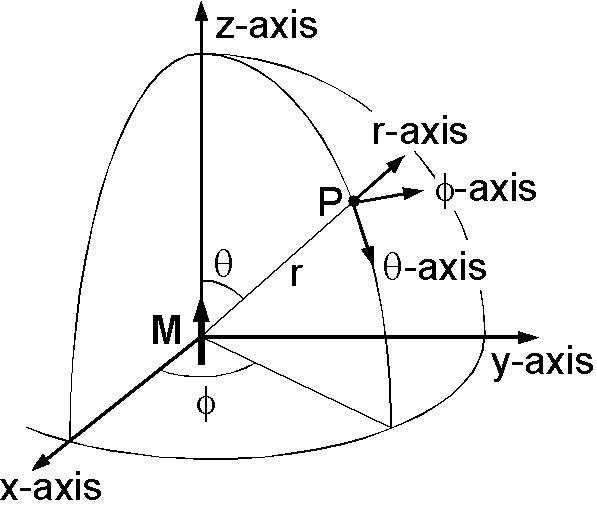
磁気双極子のポテンシャル: 右図は直交座標系 \(x\)-\(y\)-\(z\) と極座標系 \(r\)-\(\theta\)-\(\phi\) の関係を表わします.原点に位置する +\(z\) 軸方向の磁気双極子モーメント \(M\) のポテンシャルは \(\mu_0\) を真空の透磁率として(問題6-2-2で導きます), \begin{equation} W = \frac{\mu_0}{4\pi}\frac{M\cos\theta}{r^2}, \label{eq02} \end{equation} となります.式 (1) から磁場が求まりますが,この場合は極座標系における次の微分演算子を使うと簡単になります. \begin{equation} \nabla = \left(\frac{\partial}{\partial r}, \frac{1}{r}\frac{\partial}{\partial\theta}, \frac{1}{r\sin\theta}\frac{\partial}{\partial\phi}\right). \label{eq03} \end{equation} 式 (2) と (3) から (1) の \({\bf B}=-\nabla W\) を計算すると次のようになります. \[ B_r = \frac{\mu_0}{2\pi}\frac{M\cos\theta}{r^3}, \quad B_\theta = \frac{\mu_0}{4\pi}\frac{M\sin\theta}{r^3}, \quad B_\phi = 0. \] ここで上図を地球に当てはめると, \(\theta\) は点 P の緯度 \(\lambda\) の余角(余緯度)で \(\phi\) は経度(東経)です.また, \(r\)-軸, \(\theta\)-軸, \(\phi\)-軸 はそれぞれ P 点における鉛直上向き,南向き,東向きの方向です.よって,地磁気の北,東,下向き成分はそれぞれ, \(X\) = \(-B_\theta\), \(Y\) = \(B_\phi\), \(Z\) = \(-B_r\) となります.これらを考慮して \(r\) を地球半径 \(a\) とおき,地心軸双極子モーメント \(M\) による緯度 \(\lambda\) の地磁気3成分は次式となります. \begin{equation} X = -\frac{\mu_0 M\cos\lambda}{4\pi a^3}, \quad Y = 0, \quad Z = -\frac{\mu_0 M\sin\lambda}{2\pi a^3}. \label{eq04} \end{equation} 式 (4) では \(X\) と \(Z\) の負号のため,磁場は南向きで上向きとなり,前ページの式 (2) と逆になっています.これは前ページでは磁気双極子が南半球を向いている現在の地磁気を想定しているからです.
ポテンシャルのラプラス方程式: 磁場 \({\bf B}\) は,磁荷が存在しないため,次式を満たします. \[ \nabla\cdot{\bf B} = 0. \] これに式 (1) の \({\bf B} = -\nabla W\) を代入すると,ラプラス方程式とよばれる次式を得ます. \begin{equation} \nabla^2 W = 0. \label{eq05} \end{equation} ここに, \(\nabla^2\) はラプラシアンという微分演算子で,直交座標系では, \[ \nabla^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}, \] であり,極座標系では次のようになります. \[ \nabla^2 = \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial}{\partial r}\right) + \frac{1}{r^2\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial}{\partial\theta}\right) + \frac{1}{r^2\sin^2\theta}\frac{\partial^2}{\partial\phi^2}. \] これを用いて式 (5) を整理すると,次の \(W\) についての方程式となります. \begin{equation} r^2\frac{\partial^2 W}{\partial r^2} + 2r\frac{\partial W}{\partial r} + \frac{1}{\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial W}{\partial\theta}\right) + \frac{1}{\sin^2\theta}\frac{\partial^2 W}{\partial\phi^2} = 0. \label{eq06} \end{equation} この方程式は \(W\) を次のように変数分離することで解くことができます. \begin{equation} W(r,\theta,\phi) = R(r)\Theta(\theta)\Phi(\phi). \label{eq07} \end{equation} これを式 (6) に代入し \(R\Theta\Phi\) で割って整理すると, \begin{equation} \frac{r^2}{R}\frac{d^2 R}{d r^2} + \frac{2r}{R}\frac{d R}{d r} = -\frac{1}{\Theta\sin\theta}\frac{d}{d\theta}\left(\sin\theta\frac{d \Theta}{d\theta}\right) - \frac{1}{\Phi\sin^2\theta}\frac{d^2 \Phi}{d\phi^2}. \label{eq08} \end{equation} この式は, \(r\) だけの関数である左辺と \(\theta\) と \(\phi\) だけの関数である右辺が常に等しいので定数となります.そこで,式 (8) を定数 \(n(n+1)\) とおくと左辺から \(R\) についての次式を得ます. \[ \frac{d^2 R}{d r^2} + \frac{2}{r}\frac{d R}{d r} - \frac{n(n+1)}{r^2}R = 0. \] この方程式の解は \(r^n\) と \(r^{-n-1}\) ですので, \(R\) は \(A_n\) と \(B_n\) を定数として次式となります. \begin{equation} R_n(r) = A_n r^n + B_n\frac{1}{r^{n+1}}. \label{eq09} \end{equation} 定数として \(n(n+1)\) とおいた式 (8) の右辺は, \begin{equation} \frac{\sin\theta}{\Theta}\frac{d}{d\theta}\left(\sin\theta\frac{d \Theta}{d\theta}\right) + n(n+1)\sin^2\theta = -\frac{1}{\Phi}\frac{d^2 \Phi}{d\phi^2}, \label{eq10} \end{equation} となりますが,これも定数ですので \(m^2\) とおき,右辺は次の \(\Phi\) の方程式となります. \[ \frac{d^2 \Phi}{d\phi^2} + m^2\Phi = 0. \] この解は \(\cos m\phi\) と \(\sin m\phi\) ですので, \(\Phi\) は \(C_m\) と \(D_m\) を定数として次式となります. \begin{equation} \Phi_m(\phi) = C_m \cos m\phi + D_m\sin m\phi. \label{eq11} \end{equation} 最後に, \(m^2\) とおいた式 (10) の左辺から次の \(\Theta\) の方程式を得ます. \[ \frac{d^2\Theta}{d\theta^2} + \frac{\cos\theta}{\sin\theta}\frac{d\Theta}{dt} + \left(n(n+1) - \frac{m^2}{\sin^2\theta}\right)\Theta = 0. \] この方程式の解は特殊関数のルジャンドル陪関数として知られており, \begin{equation} \Theta_n^m(\theta) = P_n^m(\cos\theta), \label{eq12} \end{equation} となります.結局, \(W\) は式 (9), (11), (12) を式 (7) に代入して,次式で与えられます. \begin{equation} W = \sum_{n=0}^\infty\sum_{m=0}^n\left(A_n^m r^n + B_n^m\frac{1}{r^{n+1}}\right)\left(C_n^m\cos m\phi + D_n^m\sin m\phi\right)P_n^m(\cos\theta). \label{eq13} \end{equation}
地磁気の球関数表示: 式 (13) の \(r\) の項を除く部分を球面調和関数といい,理工学の多くの分野で使用されますが,ここでは \(r\) の項も含めて球関数ということにします.球関数は地磁気や重力など,地球表面に分布する量を表わすために使用されます.例えばある量が種々のスケールで分布しているとき,球関数の低次の項は大きなスケールの分布を,高次の項は細かい分布を表わし,それらの重ね合わせが実際の分布を表わします.これはちょうど1次元のフーリエ級数展開に似ています.例えば,時間変動する量のフーリエ級数表示では,低次の項は低周期の変動を,高次の項は高周期の変動を表わし,それらの大きさから卓越する周期成分が分かります.
ここでは,地球内部起源の地磁気を表わすポテンシャルだけを考えます.その際,式 (13) を適用するに当たり,以下の点を考慮します.
- \(1/r^{n+1}\) と \(r^n\) の項は \(r\)→\(\infty\) でそれぞれゼロと無限大に収束するので,地球内部起源としては前者のみを採用する.
- ポテンシャルが \(1/r\) に比例する単磁荷は存在しないので, \(1/r^{n+1}\) の項で \(n\) = 0 は除く.
- \(r\) は地球半径 \(a\) で規格化し, \((r/a)\) の形にすると便利である.
これらを考慮して式 (13) を書き換えると,地磁気のポテンシャルは次の形で表わせます. \begin{equation} W = a\sum_{n=1}^\infty\sum_{m=0}^n\left(\frac{a}{r}\right)^{n+1}\left(g_n^m\cos m\phi + h_n^m\sin m\phi\right)P_n^m(\cos\theta). \label{eq14} \end{equation} 係数の \(g_n^m\) と \(h_n^m\) はガウス係数とよばれ,通常 nT(10-9 T)の単位で表わします.なお,先頭の \(a\) は \(W\) を空間微分したときにガウス係数以外は無次元にするためです.また,地磁気の分野ではルジャンドル陪関数 \(P_n^m(\cos\theta)\) として,シュミットによる擬正規化された関数を使用します.
式 (14) により地磁気を球関数で表わすには,観測値から最小二乗法によりガウス係数を決定します. 19 世紀中頃にガウスはこの方法を考案し, \(n\) = 4 まで \(r^n\) の項も含めて解析しガウス係数を決定しました.その結果から,地磁気の原因がほとんど内部起源であることや,地磁気は自転軸から少し傾いた双極子磁場に近いことが初めて示されました.現在では,前ページで扱った国際標準地球磁場として5年毎にガウス係数とその年変化値が決定され,2000 年以降は \(n\) = 13 までの値を含みます.
地球上の余緯度 \(\theta\),東経 \(\phi\) の地点での磁場の3成分 \((B_r,B_\theta,B_\phi)\) は式 (3) の \(\nabla\) を式 (14) の \(W\) に作用させ, \(r\) = \(a\) とおくと求まります.さらに北,東,下向き成分, \((X,Y,Z)\) に直すと以下の通りです. \begin{eqnarray} X & = & \sum_{n=1}^\infty\sum_{m=0}^n(g_n^m\cos m\phi + h_n^m\sin m\phi)\frac{dP_n^m(\cos\theta)}{d\theta}, \nonumber \\ Y & = & \sum_{n=1}^\infty\sum_{m=0}^nm(g_n^m\sin m\phi - h_n^m\cos m\phi)\frac{P_n^m(\cos\theta)}{\sin\theta}, \label{eq15} \\ Z & = & -\sum_{n=1}^\infty\sum_{m=0}^n(n+1)(g_n^m\cos m\phi + h_n^m\sin m\phi)P_n^m(\cos\theta). \nonumber \end{eqnarray}
3次までのガウス係数表: IGRF-14( → IGRF maintained by IAGA)による 2025 年のガウス係数を nT の単位で \(n\) = \(m\) = 3 まで下表に示します. \(n\) = 1 は磁気双極子モーメントを表わします.その自転軸成分が \(g_1^0\) ですが,他の係数よりずっと大きく,負号のため南向きであることが分かります. \(g_1^1\) と \(h_1^1\) は赤道面成分で,後者の東経 90° を向いた成分が2番めに大きいです.非双極子成分は \(n\) = 2 以降,一般に次数とともに小さくなります.
| n | m | g | h | n | m | g | h | n | m | g | h | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | -29350.0 | - | 2 | 0 | -2556.2 | - | 3 | 0 | 1360.9 | - | ||||
| 1 | 1 | -1410.3 | 4545.5 | 2 | 1 | 2950.9 | -3133.6 | 3 | 1 | -2404.2 | -56.9 | ||||
| 2 | 2 | 1648.7 | -814.2 | 3 | 2 | 1243.8 | 237.6 | ||||||||
| 3 | 3 | 453.4 | -549.6 |
球面調和関数のパターン: 地球表面上で球関数が取る値の正負について,そのパターンを \(n\) の 1 から 3 まで下図に示します.図は地球を無限遠の斜め上方から見た場合の投影法で描かれ,正面は経度 315°E です.点線は赤道と 90° 毎の経線で,右手の経線が 0°E です.球関数は灰色の領域で正,白色で負,境界線上でゼロです. \(P_n^0\) はゼロとなる緯度線が \(n\) 本あり, \(n\) + 1 の領域に分かれます. \(P_n^m\cos m\phi\) は \(n\) - \(m\) 本の緯度線でゼロ, 2\(m\) 本の経線でゼロとなります. \(P_n^m\sin m\phi\) は図にはないですが, \(\cos m\phi\) のパターンを東へ 90°\(/m\) ずらした図となります.
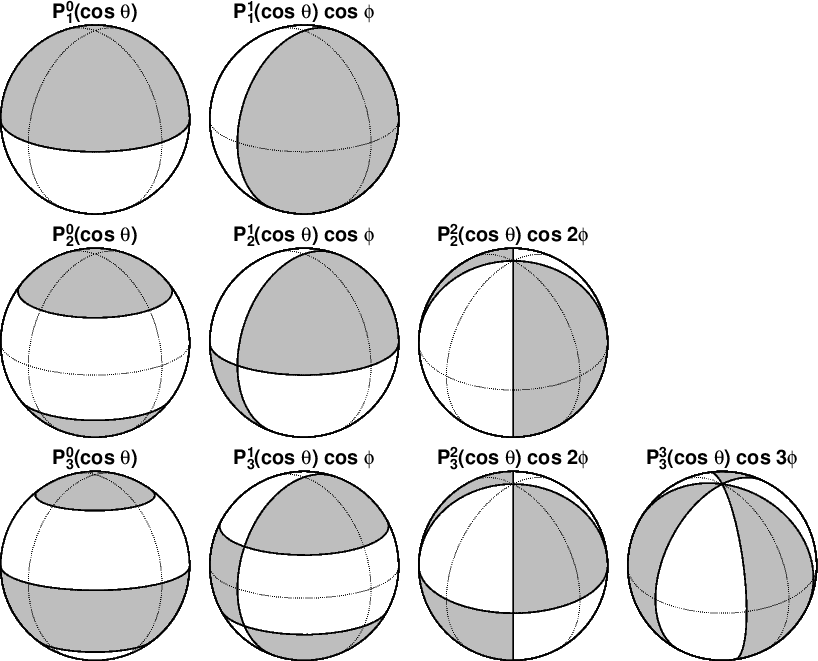
この球面調和関数のパターンと世界の磁気図(→ I, D, F 磁気図)を比較すると, \(P_1^0\) が伏角磁気図と似ていて,軸双極子成分 \(g_1^0\) が卓越していることが分かります.しかし,それ以外の項と磁気図との対応は困難です.そこで,式 (15) で \(n\) = 1 の項を除いて和を取り,非双極子磁場を磁気図として表わしてみます.下図は \(g_1^0\), \(g_1^1\), \(h_1^1\) を含まない非双極子磁場の鉛直成分の分布を表わします.図は南北で符号の異なるパターンが目立ちますが,球関数の \(P_2^1\) のパターンと似ています.実際,上記のガウス係数の表から \(g_2^1\) と \(h_2^1\) の寄与が大きいことが分かります.
問題6-2-1
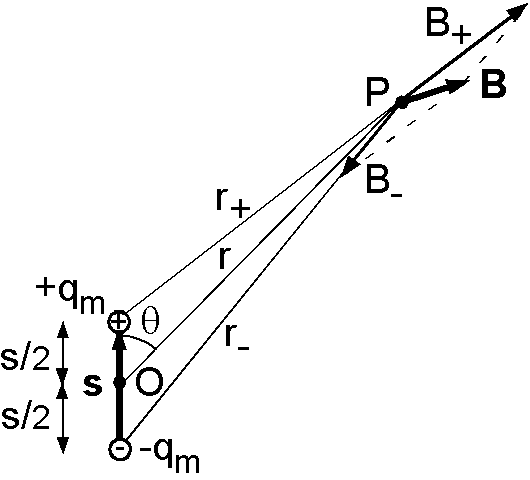
電磁気学では磁気双極子を環状の電流で表わし,電流と環の面積の積が磁気双極子モーメントで,単位は A m2 となります.これは磁荷が存在しないからです.しかし,磁荷を仮定して磁気双極子のポテンシャルを導く方法は,基礎的演習に相応しいと思われます.電荷との類似性から,一般に単磁荷 \(q_m\) による距離 \(r\) の点のポテンシャル \(W\) は,次式で表わされます. \[ W = \frac{\mu_0}{4\pi}\frac{q_m}{r}. \]
そこで,図のような距離 \(s\) 離れた正負の2つの磁荷 \(\pm q_m\) による双極子を考えます. \(-q_m\) から \(+q_m\) に向かう距離ベクトルを \({\bf s}\) とし,その中点を O とします.いま,ベクトル \({\bf s}\) の方向から角度 \(\theta\) で, O から距離 \(r\) の点 P の磁場 \({\bf B}\) は図のようなります.しかし,磁場よりはポテンシャルで考えたほうが簡単です.点 P と 正と負の磁荷との距離をそれぞれ \(r_+\) と \(r_-\) とすると,双極子による点 P のポテンシャル \(W\) は以下のようになります. \[ W = \frac{\mu_0 q_m}{4\pi}\left(\frac{1}{r_+} - \frac{1}{r_-}\right). \]
では, \(r_+\) と \(r_-\) を余弦定理で \(r\), \(\theta\), \(s\) で表わし, \(r \gg s\) として,次の \(x\) が小さいときの近似式, \[ \frac{1}{\sqrt{1 + x}} \approx 1 - \frac{x}{2}, \quad (|x| \ll 1) \] を用いて次の磁気双極子のポテンシャルを導きなさい.但し,磁気双極子モーメントをベクトルとして \({\bf M} = q_m{\bf s}\) と定義します. \[ W = \frac{\mu_0}{4\pi}\frac{M\cos\theta}{r^2} = \frac{\mu_0}{4\pi}\frac{{\bf M}\cdot{\bf r}}{r^3}. \]
問題6-2-2
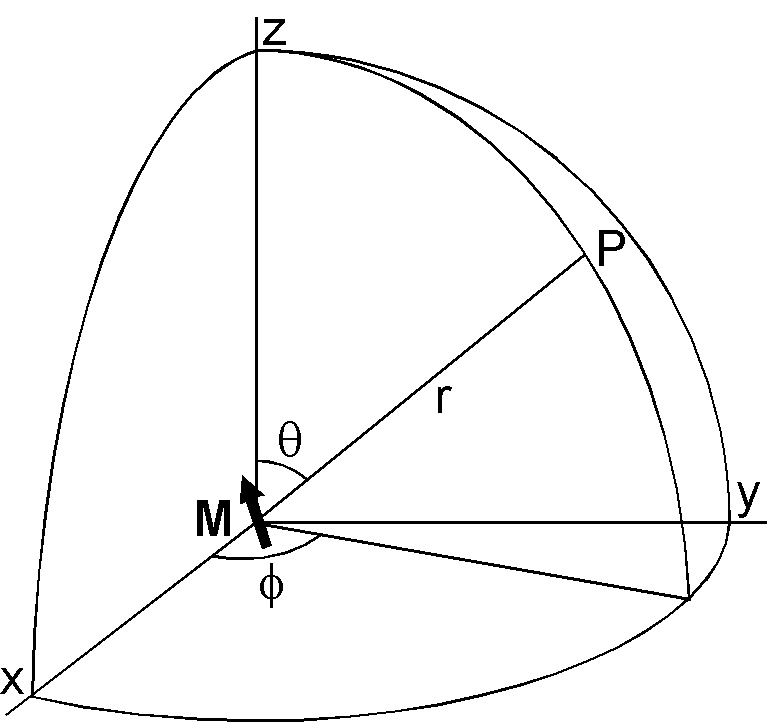
地球中心で任意の向きの磁気双極子 \({\bf M}\) による,地球上の任意の点 P における磁気ポテンシャルを考えます.直交座標と極座標を図のように取り,自転軸の北極方向を z 軸,赤道面の経度 0° を x 軸,東経 90° を y 軸とします.また, \(r\), \(\theta\), \(\phi\) はそれぞれ点 P の地球中心からの距離,余緯度,東経です.点 P での磁気ポテンシャルは \[ W = \frac{\mu_0}{4\pi}\frac{{\bf M}\cdot{\bf r}}{r^3}, \] で表わされますが,これを次のように変形します. \begin{eqnarray*} W & = & \frac{\mu_0}{4\pi}\frac{M_xx + M_yy + M_zz}{r^3}, \\ & = & \frac{\mu_0}{4\pi}\frac{M_x\sin\theta\cos\phi + M_y\sin\theta\sin\phi + M_z\cos\theta}{r^2}. \end{eqnarray*}
(1) この式と地磁気ポテンシャルの球関数表示を比較して,磁気双極子の成分 \((M_x,M_y,M_z)\) とガウス係数 \(g_1^0,g_1^1,h_1^1\) の関係を導きなさい.導出には,本文の式 (14) を n = m = 1 まで展開し, 1 次の球関数が次式で与えられることを利用します. \[ P_1^0(\cos\theta) = \cos\theta, \quad P_1^1(\cos\theta) = \sin\theta. \]
(2) 2025 年の 1 次のガウス係数は nT の単位で次の通りです. \[ g_1^0 = -29350, \quad g_1^1 = -1410, \quad h_1^1 = 4546. \] 真空の透磁率を \(\mu_0\) = 4π×10-7 N/A2,地球の半径を \(a\) = 6371 km として,磁気双極子モーメントの大きさと地磁気北極の緯度,経度を計算しなさい.
