古地磁気学と岩石磁気学の基礎

単磁区粒子の熱残留磁化：熱活性化理論

前ページで示したように，単磁区（SD）粒子の自発磁化 \(M_s\) を回転させるためには微視的保磁力 \(H_K\) よりも大きな磁場 \(H\) をかける必要があります（\(H\) が容易軸に平行な場合）．反磁場係数の公式を利用して（Stacey & Banerjee 1974），縦横比が 4/3 の回転楕円体のマグネタイト粒子の \(H_K\) は， \[ H_K = (N_p - N_l)M_s = (11/30 - 4/15)\times 480\times 10^3 = 48\times 10^3\ \mathrm{A/m} \approx 0.06\ \mathrm{T}. \] 0.06 T (60 mT) の \(H_K\) は ~0.00005 T (~50 μT) の地球磁場よりもずっと大きいですが，火山岩は古地磁気を記録することができます．これはひとつには \(M_s\) と \(H_K\) が高温では小さいからですが，より重要なこととしては，熱活性化のために \(M_s\) がエネルギーの壁を超えて回転することが容易になるためです．以下に Neel (1949) により提出された単磁区粒子の熱残留磁化（thermoremanent magnetization, TRM）に関わる熱活性化理論を説明します．ここで使用する式や記号は主に Dunlop & Ozdemir (1997) に基づいています．

熱活性化と緩和時間

高温においては，熱活性化のために \(M_s\) はある確率でエネルギーの壁を超えて回転し， \(H\) の方向へ揃います．これは典型的な緩和現象でアレニウスの式（Arrhenius' equation）で表されます．この式では，反応速度 \(K\) または緩和時間 \(\tau\) （\(K\) の逆数）がボルツマン因子（Boltzmann's factor）を用いて， \begin{equation} K = \frac{1}{\tau} = A \exp\left(-\frac{E_a}{kT}\right), \label{eq01} \end{equation} で与えられます．ここに， \(E_a\)， \(T\)， \(k\) = 1.3807×10-23 J/K はそれぞれ活性化エネルギー（エネルギーの壁），絶対温度，ボルツマン定数です． \(A\) は反応に固有の定数で，マグネタイトの磁化については， 108 ~ 1013 s-1 ですが，通常は \(A\) = 109 s-1 が使用されます．

単磁区粒子の集団を考えて，それぞれが自発磁化 \(M_s\) を持つとします．これらの粒子集団に高温で弱い磁場 \(H\) をかけたとします．高温では緩和時間 \(\tau\) が非常に短いので（例えば 1 s），ある一定の割合で \(M_s\) が \(H\) 方向に揃い，バルクの（全体としての）磁化が現れます． \(H\) を取り除くと \(M_s\) は 1 s 程のほとんど瞬時にバラバラとなりバルクの磁化は消失します．このような磁化の状態は超常磁性（スーパー常磁性， superparamagnetism）と呼ばれます．超常磁性は常磁性と似ていますが，それぞれの粒子がフェロ磁性に起因する自発磁化を持っている点で異なります．この超常磁性の状態から \(H\) をかけながら温度を下げると，バルクの磁化は \(H\) を取り除いても消失せずに残るようになります．これは \(\tau\) が温度の指数関数で表されるために低温では極めて大きくなるからです．式 (1) で \(A\) = 109 s-1， \(E_a\) = const. とした場合の \(T\) による \(\tau\) の変化の例は， \[ \tau = 1\ \mathrm{s\ at}\ T = 550°\mathrm{C}\ \longrightarrow\ \tau = 1.5768\times 10^{15}\ \mathrm{s\ (5\ 千万年)\ at}\ T = 33°\mathrm{C}. \] よって， 550°C で 1 秒で誘起された磁化は ~30°C では長大な地質学的な時間で安定となります．実際はこの例は \(E_a\) を一定と仮定したので，むしろかなり控えめな \(\tau\) の見積もりとなっています．高温では \(M_s\) と \(H_K\) は小さくなるので \(E_a\) も小さくなります．キューリー温度を \(T_C\) として， \(M_s\) と \(H_K\) の温度変化を \(\sqrt{1 - T/T_C}\) に比例するとすると， \(E_a\) ∝ \(M_s\)×\(H_k\) ∝ \((1-T/T_C)\) となります．この効果を考慮すると， \(\tau\) の変化は次のようになります． \[ \tau = 1\ \mathrm{s\ at}\ T = 550°\mathrm{C}\ \longrightarrow\ \tau = 1.5768\times 10^{17}\ \mathrm{s\ (50\ 億年)\ at}\ T = 498°\mathrm{C}. \] よって， \(T\) が ~50°C 低下することで， \(\tau\) は地球の年齢より長くなります．この超常磁性の磁化が固定される現象を磁化のブロッキング（blocking）といい，磁化が実際に固定される温度をブロッキング温度（blocking temperature） \(T_B\) といいます．

↑ ページ冒頭

TRM の熱活性化理論（Neel 1949）

体積が \(V\) で自発磁化 \(M_s\) を持つ回転楕円体の単磁区粒子を考えます．前ページで記したように，磁場 \(H\) を容易軸に沿ってかけた場合の全磁気エネルギー \(E\) は， \begin{equation} E = \mu_0 V M_s H_K\left(-(H/H_K)\cos\theta + {\tiny \frac{1}{2}}\sin^2\theta\right), \label{eq02} \end{equation}

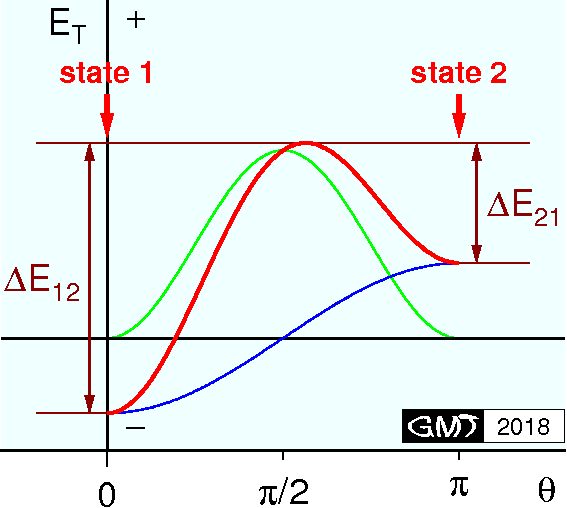
単磁区粒子の自発磁化に対するエネルギーの壁．
で表され，ここに \(\theta\) は \(M_s\) の容易軸からの振れの角度です．小さな正の \(H\) (0 < \(H\) < \(H_K\)) に対する \(E-\theta\) 曲線を右図に示します． \(M_s\) が \(\theta\) = 0 と π の状態を，それぞれ状態 1 と 2 とすると（図の赤い矢印），次式を得ます． \begin{eqnarray*} E_1 & = & -\mu_0 V M_s H, \\ E_2 & = & \mu_0 V M_s H, \\ E_{max} & = & {\tiny \frac{1}{2}}\mu_0 V M_s H_K\left(1 + (H/H_K)^2\right). \end{eqnarray*} エネルギーの壁は，0 \(\rightarrow\) π と π \(\rightarrow\) 0 を，それぞれ \(\Delta E_{12}\) と \(\Delta E_{21}\) で表すと，次式のようになります． \begin{eqnarray} \Delta E_{12} &=& E_{max}-E_1 = {\tiny \frac{1}{2}}\mu_0 V M_s H_K\left(1+H/H_K\right)^2, \label{eq03} \\ \Delta E_{21} &=& E_{max}-E_2 = {\tiny \frac{1}{2}}\mu_0 V M_s H_K\left(1-H/H_K\right)^2. \label{eq04} \end{eqnarray}

ここで，このような単磁区粒子の \(N\) 個の集団を考えます．熱エネルギーの入力がない場合は，それぞれの粒子の \(M_s\) は最初の位置，状態 1 または 2，に留まります．熱活性化が加わると，いくつかの粒子では \(M_s\) がエネルギーの壁を超えて回転することとなります．エネルギーの壁は 2 \(\rightarrow\) 1 (π \(\rightarrow\) 0) の方が 1 \(\rightarrow\) 2 (0 \(\rightarrow\) π) よりも低いので， 回転 2 \(\rightarrow\) 1 の方が 1 \(\rightarrow\) 2 よりも頻繁に発生します．最終的には，状態 1 (+\(M_s\)) の粒子の数が状態 2 (-\(M_s\)) よりも多くなり， \(N\) 個の粒子全体の磁化は正となり， \(H\) 方向へ揃うことになります．

\(n\) 個の粒子が状態 1 に， \(N-n\) 個が状態 2 にあるとします． \(n\) の時間微分は次式で表されます． \begin{equation} \frac{dn}{dt} = K_{21}(N-n) - K_{12}n = \frac{N-n}{\tau_{21}} - \frac{n}{\tau_{12}}, \label{eq05} \end{equation} ここに， \(K_{21}\) と \(K_{12}\) (\(\tau_{21}\) と \(\tau_{12}\)) はそれぞれ \(M_s\) の 2 \(\rightarrow\) 1 と 1 \(\rightarrow\) 2 の回転に関わる反応速度（緩和時間）です．次のように \(\tau\) を導入すると， \begin{equation} \frac{1}{\tau} = \frac{1}{\tau_{12}} + \frac{1}{\tau_{21}}, \label{eq06} \end{equation} 式 (5) は次のように表されます． \[ \frac{dn}{dt} = \frac{1}{\tau_{21}}N - \frac{1}{\tau}n. \] これを積分すると， \[ \log\left(\frac{1}{\tau}n - \frac{1}{\tau_{21}}N\right) = -\frac{t}{\tau} + C, \\ n = C'\tau e^{-t/\tau} + \frac{\tau}{\tau_{21}}N, \] ここに， \(C\) と \(C'\) は積分定数です．正の磁化に寄与する粒子の数は \(2n-N\) なので， \begin{eqnarray*} 2n-N & = & 2C'\tau e^{-t/\tau} + \left(\frac{2\tau}{\tau_{21}} -1\right)N, \\ & = & 2C'\tau e^{-t/\tau} + \frac{\tau_{12}-\tau_{21}}{\tau_{12}+\tau_{21}}N. \end{eqnarray*} \(N\) 個の粒子の平均の磁化は， \begin{eqnarray*} M & = & \frac{2n-N}{N}M_s, \\ & = & \frac{2C'\tau}{N}M_s e^{-t/\tau} + \frac{\tau_{12}-\tau_{21}}{\tau_{12}+\tau_{21}}M_s. \end{eqnarray*} 初期状態 (\(t\) = 0) と平衡状態 (\(t\) = ∞) の磁化をそれぞれ， \(M_0\) と \(M_{eq}\) と記すと， \begin{eqnarray} M_0 & = & M(0) = \frac{2C'\tau}{N}M_s + \frac{\tau_{12}-\tau_{21}}{\tau_{12}+\tau_{21}}M_s, \nonumber \\ M_{eq} & = & M(\infty) = \frac{\tau_{12}-\tau_{21}}{\tau_{12}+\tau_{21}}M_s. \label{eq07} \end{eqnarray} よって，次式を得ます． \begin{equation} M = (M_0 - M_{eq})e^{-t/\tau} + M_{eq} = M_0 e^{-t/\tau} + M_{eq}(1 - e^{-t/\tau}). \label{eq08} \end{equation} 式 (8) は，緩和時間 \(\tau\) が観測時間 \(t\) より極めて長い場合は（\(\tau \gg t\)）， \(M\) は初期状態 \(M_0\) に留まり， \(\tau\) が \(t\) より極めて短い場合は（\(\tau \ll t\)）， \(M\) は式 (7) で与えられる \(M_{eq}\) に到達することを示しています．

アレニウスの式 (1) の活性化エネルギー \(E_a\) に (3) と (4) のエネルギーの壁 \(\Delta E_{12}\) と \(\Delta E_{21}\) を代入すると， (7) の平衡に達した磁化 \(M_{eq}\) は以下のように変形されます． \begin{eqnarray} M_{eq} &=& \frac{\tau_{12}-\tau_{21}}{\tau_{12}+\tau_{21}}M_s, \nonumber \\ &=& \frac{\exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1+\frac{H}{H_K}\right)^2\right] -\exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1-\frac{H}{H_K}\right)^2\right]} {\exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1+\frac{H}{H_K}\right)^2\right] +\exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1-\frac{H}{H_K}\right)^2\right]}M_s, \nonumber \\ &=& \frac{\exp\left(\frac{\mu_0VM_sH}{kT}\right)-\exp\left(-\frac{\mu_0VM_sH}{kT}\right)} {\exp\left(\frac{\mu_0VM_sH}{kT}\right)+\exp\left(-\frac{\mu_0VM_sH}{kT}\right)}M_s, \nonumber \\ &=& M_s\tanh\left(\frac{\mu_0VM_sH}{kT}\right). \label{eq09} \end{eqnarray} これが \(\tau\) が観測時間 \(t\) よりずっと短い高温で \(H\) により誘起された磁化です．その後の冷却により， 式 (9) の hyperbolic tangent の項はブロッキング温度 \(T_B\) で一定となり，磁化は固定されます．さらに室温 \(T_0\) まで冷却すると， \(M_s\) の項だけが \(T_0\) の値に増加します．それ故， \(T_0\) での磁化は次式で表されます． \begin{equation} M(T_0) = M_s(T_0)\tanh\left(\frac{\mu_0VM_s(T_B)H}{kT_B}\right). \label{eq10} \end{equation} これが室温で観測される TRM となります．この理論は容易軸方向が揃った単磁区粒子集団について導かれたので，ランダムな方向の粒子集団については， Neel (1949) は (10) の結果に \(1/3\) を掛けることとしました．厳密には，ランダムな方向の場合は， \(M\) はランジュバン関数（Langevin function）で与えられますが（常磁性の理論と同様に），小さな \(H\) についての近似式は次のように両理論で同一となります． \[ M(T_0)/M_s(T_0) \approx \frac{\mu_0 V M_s(T_B)}{3k T_B}H. \] この関係式は，磁場が弱い場合には TRM の強度はかけられた磁場の強さに比例することを示しています．これが古地磁気の強度（古地磁気強度，古地球磁場強度， paleointensity）を求める方法の基礎となっています．

↑ Top of this page

ブロッキング温度と冷却速度

ブロッキング温度 \(T_B\) は緩和時間 \(\tau\) が冷却の特徴的な時間 \(t\) に等しくなる温度と定義されるのが通常です．しかし，特徴的な時間 \(t\) は実験室の実験では ~60 s かもしれないし，厚い溶岩流の冷却では ~1 年かもしれません．ここでは， \(T_B\) は緩和時間 \(\tau\) が 1°C 冷却する時間，即ち \(|dT/dt|^{-1}\) に等しくなる温度と定義することにします．しかし，磁化は温度 \(T_B\) で瞬時にブロッキングされるのではなく， \(T_B\) の上下のある一定の温度幅で進行します．それ故，式 (8) により冷却速度が遅いほどブロッキングはより長い時間で進行し，ブロックされる磁化もより大きくなります．下図は温度が階段状に低下するとした場合のマグネタイトの単磁区粒子についてのシミュレーションです．それぞれのステップで温度を一定時間保ち，その間の \(M\) の増加を (8) を使用して計算しました．但し， \(M\) は \(M_s\) で規格化した値，即ち (9) の hyperbolic tangent の項の値です．単磁区粒子は 550°C で \(\tau\) = 1 s で平衡に達しており，即ち超常磁性の状態にあるとしてシミュレーションを開始しました．図で，赤と青の線はそれぞれ 1°C あたり 60 s と 10 s の遅い冷却と速い冷却の結果を示します（室温までの冷却時間がそれぞれ~9 時間と ~1.5 時間）．階段状の緑の線はそれぞれのステップの温度で無限時間経た時の平衡の \(M\) です．上で定義した \(T_B\) は，遅い冷却と速い冷却でそれぞれ 544°C と 547°C で， 後者は 50% ブロックされる温度とほとんど同じです．温度がさらに数度低下すると 95% のブロッキングが達成されます．

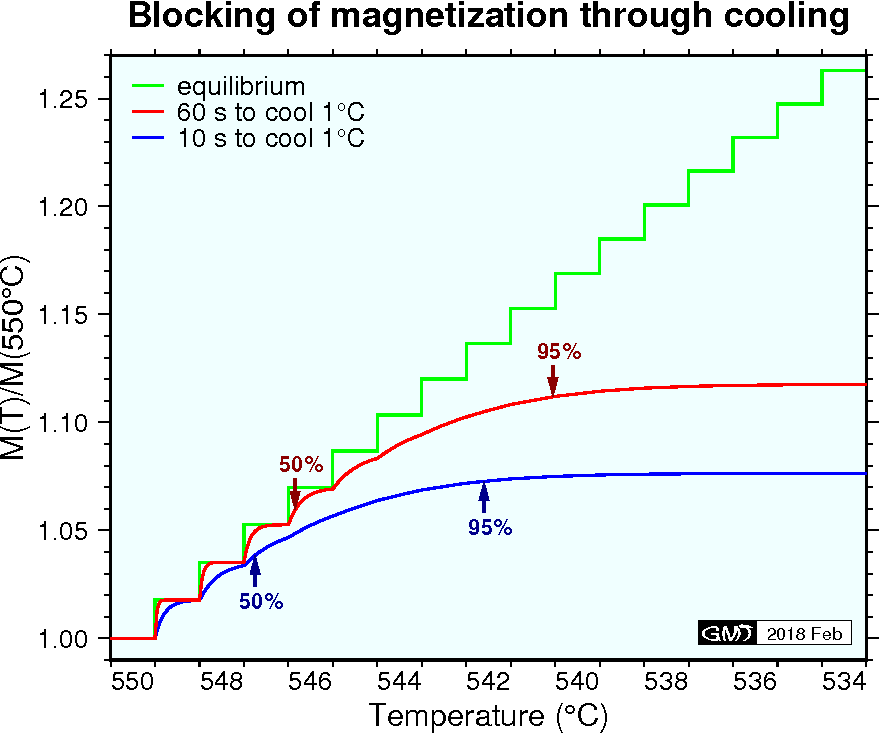
ブロッキング温度前後での磁化のブロッキングを２つの異なる冷却速度についてシミュレーションした結果．

上のシミュレーションの結果は冷却が連続して進行する実際のブロッキング過程とは異なるかもしれません．しかし，ブロッキング温度が冷却速度と初期状態の温度に大変依存することは火山岩の TRM についてよく知られています．キューリー温度 \(T_C\) 直下の高温からの冷却では，磁化は 2 ~ 3 度の狭い温度範囲でブロッキングされます．

参考文献：

↑ ページ冒頭   ← 前ページ   → 次ページ