物質の磁性:原子の磁気モーメント
全ての物質は3種の磁気的性質である反磁性・常磁性・強磁性のいずれかを示します.反磁性の物質は棒磁石から跳ね返されますが,実際にはその力は微弱なので感度の高い磁力計でのみ測定できます.常磁性の物質は棒磁石から弱く引きつけられますが,やはりこの力も磁力計でのみ測定されます.強磁性の物質は棒磁石から容易に引きつけられます.これらの磁性の違いは物質を構成している原子の磁気的状態の現れです.以下に基礎レベルの物理学の範囲で原子の磁気を簡単に解説しますが,正確な理解のためには高度の量子力学が必要です.
原子の磁気モーメントは電子の軌道運動とスピン(自転)運動が原因です.量子力学では,電子の軌道角運動量 \({\bf L}\) は量子化され,その大きさは次式で与えられます. \begin{equation} |{\bf L}| = \sqrt{l(l + 1)} \hbar \quad (l = 0, 1, \cdots, n-1) \label{eq01} \end{equation} ここに, \(l\) は軌道量子数(orbital quantum number)でゼロまたは整数で, \(\hbar\) = 1.0546×10-34 J s はプランク定数です. \(n\) は全量子数(total quantum number)で電子が \(n\) 番目の殻に存在することを示します.磁場が原子に当てられると, \({\bf L}\) の磁場方向(\(z\)-軸とする)の成分も量子化され次式で与えられます. \begin{equation} L_z = m_l \hbar \quad (m_l = -l, -l+1, \cdots, 0, \cdots, l-1, l), \label{eq02} \end{equation} ここに \(m_l\) は磁気量子数(magnetic quantum number)です.電子のスピン角運動量 \({\bf S}\) も量子化され,その大きさは, \begin{eqnarray} |{\bf S}| & = & \sqrt{s(s + 1)} \hbar \quad (s = \frac{1}{2}), \label{eq03} \\ & = & \frac{\sqrt{3}}{2} \hbar, \nonumber \end{eqnarray} であり,その磁場方向の成分は次式となります. \begin{eqnarray} S_z & = & m_s \hbar \quad (m_s = \pm\frac{1}{2}), \label{eq04} \\ & = & \pm\frac{1}{2} \hbar, \nonumber \end{eqnarray} ここに \(s\) と \(m_s\) それぞれスピン量子数(spin quantum number)とスピン磁気量子数(spin magnetic quantum number)です.
量子化された角運動量のために,原子の磁気モーメント \({\bf m}\) も量子化され,その最小単位はボーア磁子(Bohr magneton) \(m_B\) で,次式で与えられます. \begin{equation} m_B = \frac{e \hbar}{2m_e} = 9.2732\times10^{-24}\ \mathrm{A\,m^2}, \label{eq05} \end{equation} ここに \(e\) と \(m_e\) は電子の電荷と質量です. \(m_B\) を用いて,軌道磁気モーメントの大きさと \(z\)-成分は, \begin{eqnarray} |{\bf m}^{\mathrm{ORB}}| & = & m_B \sqrt{l(l+1)}, \label{eq06} \\ m^{\mathrm{ORB}}_z & = & -m_B m_l. \label{eq07} \end{eqnarray} となります.スピン磁気モーメントの大きさと \(z\)-成分は次式となります. \begin{eqnarray} |{\bf m}^{\mathrm{SPIN}}| & = & 2 m_B \sqrt{s(s+1)}, \label{eq08} \\ m^{\mathrm{SPIN}}_z & = & -2 m_B m_s. \label{eq09} \end{eqnarray} (6) と (7) の軌道磁気モーメントと (8) と (9) のスピン磁気モーメントでは係数が2だけ異なることには注意が必要です.1個の電子については, \(|{\bf m}^{\mathrm{SPIN}}|\) と \(m^{\mathrm{SPIN}}_z\) はそれぞれ \(\sqrt{3}m_B\) と \(\mp m_B\) となります.
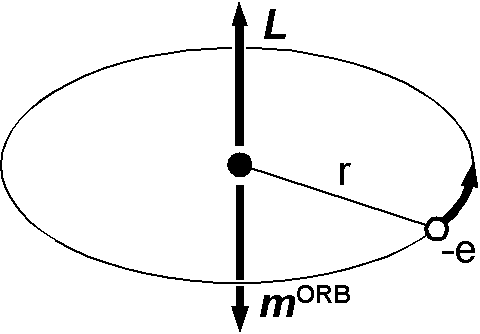
(5) のボーア磁子は図のように原子のボーアモデルを用いた古典的考察からも得ることができます.環状の電流にその面積を掛けると磁気モーメントとなるので, \begin{eqnarray*} |{\bf m}^{\mathrm{\mathrm{ORB}}}| & = & (\mathrm{current})\times(\mathrm{area}) \\ & = & (e \cdot \frac{\omega}{2\pi})(\pi r^2) = \frac{e \omega r^2}{2}, \end{eqnarray*} ここに \(\omega\) と \(r\) それぞれ電子の角速度と軌道半径です.電子の角運動量は, \[ |{\bf L}| = m_e \omega r^2. \] となるので, \(\omega\) と \(r\) をこれらの2つの式から消去し, (1) を用いると次式からボーア磁子が得られます. \[ |{\bf m}^{\mathrm{ORB}}| = \frac{e}{2m_e}|{\bf L}| = \frac{e\hbar}{2m_e}\sqrt{l(l+1)}. \]
軌道とスピンの角運動量はベクトルとして合成されて全角運動量 \({\bf J} = {\bf L} + {\bf S}\) を形成します.この角運動量のベクトル合成は原子中の全ての電子に適用されます.その際,それぞれの電子の量子数の組み合わせは同一になってはなりません(パウリの禁則律, Pauli's exclusion principle).合成された磁気モーメント \({\bf m}^{\mathrm{TOTAL}}\) の大きさと \(z\)-成分は,ランデ \(g\) 係数(Land\({\acute e}\) \(g\) factor)と合成された量子数 \(J\) と \(M_J\) を用いて次式で与えられます. \begin{eqnarray} |{\bf m}^{\mathrm{TOTAL}}| & = & g m_B \sqrt{J(J+1)}, \label{eq10} \\ m^{\mathrm{TOTAL}}_z & = & -g m_B M_J. \label{eq11} \end{eqnarray} \(g\), \(J\), \(M_J\) の値は複雑な公式を用いて計算されますが, \(g\) は通常 1(軌道のみが寄与)と 2(スピンのみが寄与)の間の値となります.
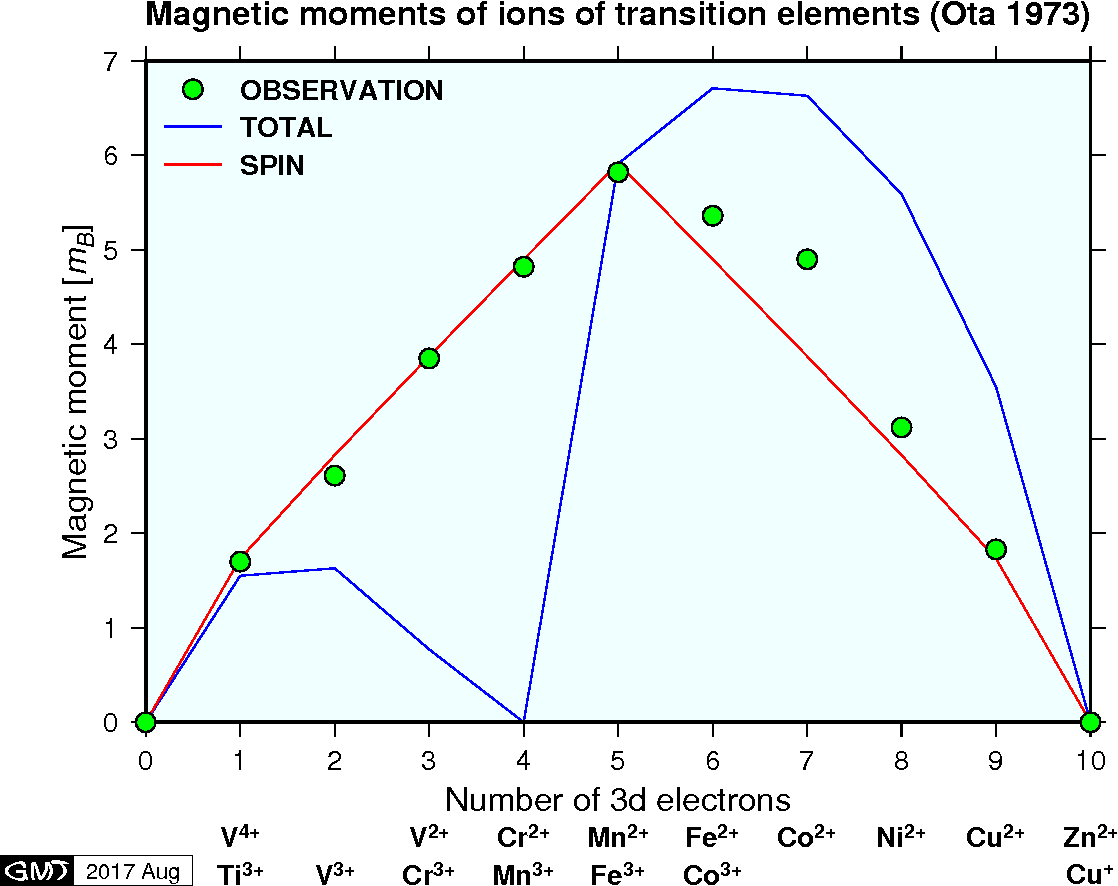
最外殻が電子で満たされている原子では軌道角運動量もスピン角運動量も消失します.そのため, He や Ne のような希ガスの原子では磁気モーメントは現れません.原子によっては, \({\bf L}\) と \({\bf S}\) が打ち消し合って \({\bf J} = {\bf 0}\) となり,磁気モーメントがゼロとなります.原子の多くでは磁気モーメントは \(m_B\) の2~3倍の大きさです.遷移元素のような幾つかの元素のグループでは,より大きな磁気モーメントが現れ, \(m_B\) の数倍となります.また,多くの原子で種々の原因から軌道角運動量の寄与が消失することがあり,そのため原子の磁気モーメントの主要な原因はスピンです.下図は遷移元素のイオンについて実験で測定した磁気モーメントを示します(太田, 1973).図で,測定データは TOTAL の曲線(\(g m_B\sqrt{J(J+1)}\))よりもむしろ SPIN の曲線(\(2m_B\sqrt{S(S+1)}\))により合っていることが分かります.これは \({\bf L}\) の寄与がほとんどゼロであることを示します.
いずれにせよ,多くの原子の磁気モーメントの大きさは \(m_B\) の2~3倍から数倍であり,熱擾乱に比較して極めて小さい値です.それ故,多くの原子は反磁性か常磁性のいずれかを示します.元素が強磁性を示すのはある種のメカニズムが働くからで,次ページ以降に示します.
参考文献:
- 太田恵造, 磁気工学の基礎 I --磁気の物理--, 215 pp., 共立出版, 東京, 1973.