単磁区粒子の熱残留磁化:単磁区粒子の磁気ヒステリシス
磁気ポテンシャル・エネルギーと静磁エネルギー
一様な磁化 \({\bf M}\) を持つ小さな磁性粒子を考えます.このような粒子を単磁区(single-domain, SD)粒子と呼ぶのに対して,2つ以上の向きの異なる磁化の領域からなる粒子は多磁区(multidomain, MD)粒子と呼ばれます.この単磁区粒子に磁場 \({\bf H}\) をかけると,磁気ポテンシャル・エネルギー \(E_m\) は, \begin{equation} E_m = -\mu_0V{\bf M}\cdot {\bf H}, \label{eq01} \end{equation} で表されます.ここに \(V\) は粒子の体積です.このエネルギーのために,磁化 \({\bf M}\) は \(E_m\) が最小となるように \({\bf H}\) の方向へ向くことになります.
一方,磁性粒子は磁気異方性(magnetic anisotropy)を持ち,磁化 \({\bf M}\) は磁気異方性エネルギーが最小になるように,1つまたは複数の容易軸と呼ばれる方向を向こうとします.磁気異方性は粒子の形状,結晶構造,結晶内の応力から生じます.ここからは,単磁区粒子では一般に最も支配的な形状磁気異方性のみを考えます.
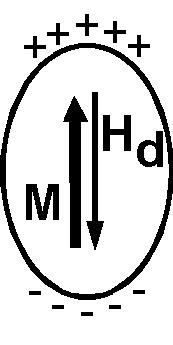
回転楕円体の形をした単磁区粒子が長軸(容易軸)方向の磁化を持っているとします.外部磁場がかからなくても粒子の内部には磁場が存在し,これを反磁場(demagnetizing field) \({\bf H_d}\) といいます.反磁場 \({\bf H_d}\) は磁化 \({\bf M}\) により誘起された表面の磁極により発生します. \({\bf H_d}\) は \({\bf M}\) と逆向きで, \[ {\bf H_d} = -N{\bf M}, \] で与えられます.ここに, \(N\) は反磁場係数(demagnetizing factor)です.反磁場 \({\bf H_d}\) は磁化 \({\bf M}\) にかかるので,式 (1)に従いもう一つのエネルギーが生じます.しかし, \({\bf H_d}\) は \({\bf M}\) 自身により誘起されるので,エネルギーの式は,磁化の微小増加 \(dM\) によるエネルギーの微小増加 \(dE\) を積分することで求める必要があります; \[ dE = -\mu_0 V dM H_d = \mu_0 V N M dM. \] これを積分して, \[ E = {\scriptsize \frac{1}{2}}\mu_0 V N M^2. \] このエネルギーは静磁エネルギー(magnetostatic energy)と呼ばれ,任意の粒子形状と磁化方向に拡大した式は, \begin{equation} E_d = {\scriptsize \frac{1}{2}}\mu_0 V{\bf M}\cdot{\bf N}\cdot{\bf M}, \label{eq02} \end{equation} となります.ここに \({\bf N}\) は反磁場テンソルです(Dunlop & Ozdemir 1997).静磁エネルギー \(E_d\) が単磁区粒子の形状磁気異方性の原因です.
磁場中における磁化の回転
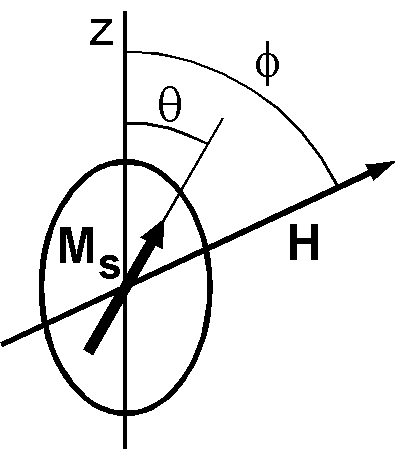
体積 \(V\) の扁長な回転楕円体の単磁区粒子を考えます.粒子は長軸(容易軸)方向に自発磁化(spontaneous magnetization) \({\bf M_s}\) を持ち,その向きに \(+z\) 軸を取ります.右図は,磁場 \({\bf H}\) を \(z\) 軸から角度 \(\phi\) の方向へかけたとき,角度 \(\theta\) 回転した磁化 \({\bf M_s}\) を示します.式 (2) を使用して,単磁区粒子の静磁エネルギー \(E_d\) は, \[ E_d = {\scriptsize \frac{1}{2}}\mu_0 V({M_s}_x,{M_s}_y,{M_s}_z) \left(\begin{array}{ccc} N_p & 0 & 0 \\ 0 & N_p & 0 \\ 0 & 0 & N_l \end{array}\right) \left(\begin{array}{c} {M_s}_x \\ {M_s}_y \\ {M_s}_z \end{array}\right), \] となります.ここに, \(N_l\) と \(N_p\) はそれぞれ \(z\) と \(x\), \(y\) 軸方向の反磁場係数です.式を変形して, \(E_d\) は次のように簡略化されます. \[ E_d = {\scriptsize \frac{1}{2}}\mu_0 V(N_p - N_l)M_s^2\sin^2\theta + {\scriptsize \frac{1}{2}}\mu_0 V N_l M_s^2. \] 反磁場係数の関係式, \(N_x + N_y + N_z = 1\),を利用すると第1項の \(N_p - N_l\) は次のようになります. \[ N_p - N_l = (1 - N_l)/2 - N_l = (1 - 3N_l)/2. \] 球では, \(N_x = N_y = N_z = \frac{1}{3}\) であることを考慮すると, \(N_p\) > \({1 \over 3}\) で \(N_l\) < \({1 \over 3}\) であることが分かります.よって, \(N_p - N_l\) は正であり,最大で \({1 \over 2}\) です.また,上の \(E_d\) の第2項は \(\theta\) に対して一定ですので省略できます.よって, \(E_d\) は次のようになります. \begin{equation} E_d = {\scriptsize \frac{1}{2}}\mu_0 V(N_p - N_l)M_s^2\sin^2\theta. \label{eq03} \end{equation} この式から \(E_d\) は常に正で, \(\theta=0\) と \(\pi\) で最小であり,そのため \(z\)-軸が \({\bf M_s}\) の容易軸となっていることが分かります.
単磁区粒子の全エネルギー \(E_T\) は (1) の磁気ポテンシャル・エネルギー \(E_m\) と (3) の静磁エネルギー \(E_d\) の和となります; \begin{equation} E_T = -\mu_0 V M_s H\cos(\phi - \theta) + {\scriptsize \frac{1}{2}}\mu_0 V(N_p - N_l)M_s^2\sin^2\theta. \label{eq04} \end{equation} \(dE_T/d\theta\) = 0 と \(d^2E_T/d\theta^2\) > 0 を満たす \(\theta\) が \(E_T\) を最小にする解,即ち,磁場 \({\bf H}\) に対して \({\bf M_s}\) が釣り合う方向となります.よって,解くべき方程式は次のようになります. \begin{eqnarray} \frac{dE_T}{d\theta} & = & \mu_0 V M_s\left(H\sin(\theta-\phi) + {\scriptsize \frac{1}{2}}(N_p - N_l)M_s\sin 2\theta\right) = 0, \label{eq05} \\ \frac{d^2E_T}{d\theta^2} & = & \mu_0 V M_s\left(H\cos(\theta-\phi) + (N_p - N_l)M_s\cos 2\theta\right) > 0. \label{eq06} \end{eqnarray}
磁場が容易軸に平行な場合
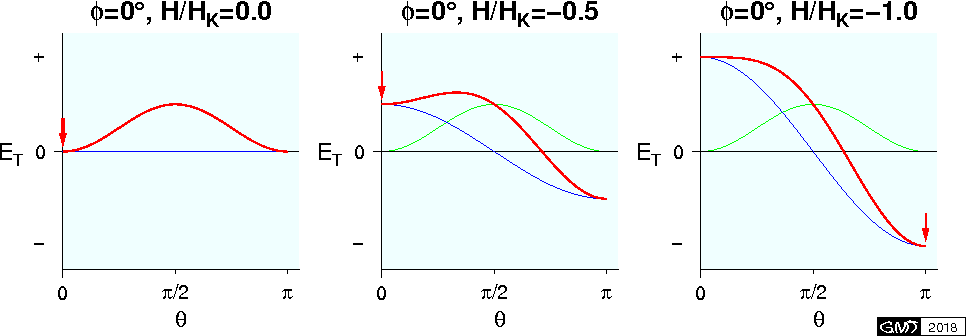
方程式 (5) と (6) の解析解が得られるのは \(\phi=0\) と \(\pi/2\) の場合だけです.\(\phi=0\) の場合は,方程式 \(dE_T/d\theta=0\) は次のようになります. \[ \mu_0 V M_s \sin\theta\left(H + (N_p - N_l)M_s \cos\theta\right) = 0. \] この方程式の解は, \begin{eqnarray*} & |H/H_K| < 1: & \quad 0, \quad \pi, \quad \theta_c = \cos^{-1}(-H/H_K), \\ & |H/H_K| \geq 1: & \quad 0, \quad \pi, \end{eqnarray*} となります.ここに, \(H_K\) を次のように導入しました. \begin{equation} H_K = (N_p - N_l)M_s. \label{eq07} \end{equation} \(d^2E_T/d\theta^2\) の正負を調べることで, \(|H/H_K|\) < 1 の場合, \(\theta=0\) と \(\pi\) で \(E_T\) は極小に, \(\theta_c\) で極大になることが分かります. \(|H/H_K|\) ≥ 1 の場合については, \(H\) ≥ \(H_K\) のときは \(\theta=0\) で, \(H\) ≤ \(-H_K\) のときは \(\theta=\pi\) で, \(E_T\) が極小になります.これらの結果から分かることは,最初に \(\theta=0\) に位置していた \({\bf M_s}\) に小さな負の磁場(\(H\) < 0)をかけ次第にその強さを増したとき, \({\bf M_s}\) は \(H\) が \(-H_K\) に達するまで元の位置にとどまり,その時点で突然 \(\theta=\pi\) へ向きを変えることです.この様子は,強さを次第に増した3つの \(H\) についての次の \(E_T\)-\(\theta\) 曲線に示されています.ここに,青,緑,赤の曲線はそれぞれ \(E_m\), \(E_d\), \(E_T\) を表します.また, \({\bf M_s}\) の平衡の位置を赤い矢印で示しました.
単磁区粒子の磁気ヒステリシス曲線
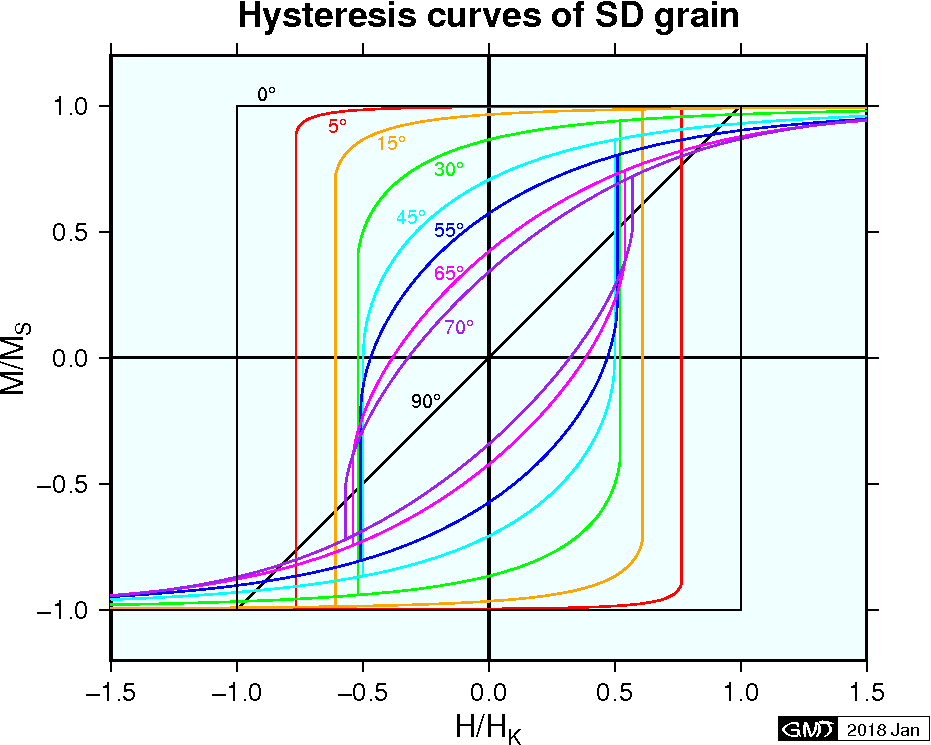
\({\bf M_s}\) は \(H\) ≤ \(-H_K\) により一旦 \(\theta=0\) から \(\pi\) へ反転すると, \(H\) ≥ \(+H_K\) がかかるまでは \(\theta=\pi\) に留まります.この現象は磁気ヒステリシスと呼ばれ, (7)で与えられる \(H_K\) は微視的保磁力(microscopic coercivity (coercive force))です.ここで, \({\bf H}\) 方向に沿って \({\bf M}\) を測定するときに,最初に \(+M_s\) から始め, \(H\) を次のように変化させたとします; \(H=0\) \(\rightarrow\) \(H\) < \(-H_K\) \(\rightarrow\) \(H=0\) \(\rightarrow\) \(H\) > \(+H_K\) \(\rightarrow\) \(H=0\).このような測定により四角い形の \(M\)-\(H\) 曲線が得られます.一般に,このような曲線はヒステリシス曲線(ループ)と呼ばれ,その形は下図のように \(\phi\) に依存します. \({\bf M_s}\) の向きを瞬時に変えるために必要な最小の \(H\) は \(\phi=\pi/4\) のときの \(H_K/2\) であることが知られています.
磁場が容易軸に直角な場合
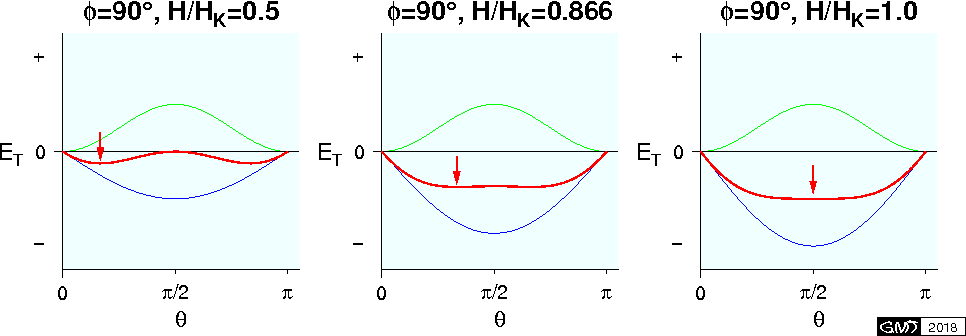
方程式 (5) と (6) のもう一つの解析解は \(\phi=\pi/2\) の場合で,上図に示されたように \(M\) と \(H\) の関係は直線となります.このことは次のように容易に示されます. \(dE_T/d\theta=0\) と \(d^2E_T/d\theta^2\) > \(0\) を満たす \(\theta\) は次のとおりです. \[ \theta_c = \sin^{-1}(H/H_K) \quad \left(|H/H_K| \leq 1\right). \] \(M\) は \({\bf H}\) 方向に沿って測定するので,次のように \(M\) と \(H\) の直線関係が得られます. \[ M = M_s\cos\left({\scriptsize \frac{\pi}{2}} - \theta_c\right) = M_s\sin\theta_c = (M_s/H_K)H. \] \(\phi=\pi/2\) の場合の \(E_T\)-\(\theta\) 曲線を3つの \(H\) について下図に示します.図で青,緑,赤の曲線はそれぞれ \(E_m\), \(E_d\), \(E_T\) で,赤い矢印は \({\bf M_s}\) の平衡の位置を示します.
ランダムな方向分布の単磁区粒子集団の磁気ヒステリシス曲線
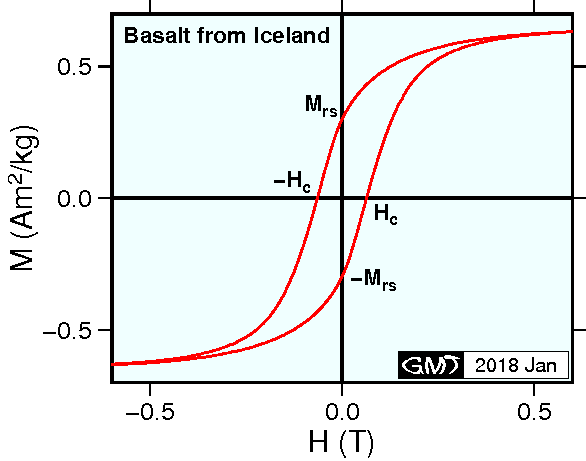
ランダムな方向分布を持つ単磁区粒子集団のバルクの \(M\)-\(H\) 曲線は,全ての \(\phi\) に対する曲線の平均となります.このような物質の \(M\)-\(H\) 曲線は,右図に示したアイスランドの玄武岩試料の測定結果に近いと考えられます.通常は岩石に含まれる磁性鉱物は擬似単磁区(pseudo-single-domain, PSD)粒子と呼ばれる小さな多磁区粒子ですが,この試料に含まれる磁性鉱物は単磁区粒子のようです. \(M\)-\(H\) 曲線において曲線と \(H\)-軸との交点,即ち \(M\) をゼロにするに必要な \(H\) が保磁力(coercivity (coercive force)) \(H_c\) です.単磁区粒子集団の保磁力 \(H_c\) は,1つの単磁区粒子の全ての \(\phi\) における保磁力(\(\phi=0\) の \(H_K\) から \(\phi=\pi/2\) のゼロ)の平均で,微視的保磁力 \(H_K\) のおよそ \(1 \over 2\) であることが知られています.
\(H=0\) における残留磁化を飽和残留磁化(saturation remanence) \(M_{rs}\) といいます. \(M_{rs}\) は理論的には \(M_s\) の \(1 \over 2\) ですが,これは以下のように示されます.磁場 \(H\) を \(H_{max}\) から \(0\) にしたとき,各単磁区粒子の \({\bf M_s}\) は容易軸上で \(H\) 方向に近い向きで残ることになります.よって, \(M_{rs}\) は \(M_s\cos\phi\) を \(H\) 方向を中心とする半球面上で平均することで得られます; \[ M_{rs} = \left.\int_0^{\pi \over 2} M_s\cos\phi\sin\phi d\phi\right/\int_0^{\pi \over 2} \sin\phi d\phi = {\scriptsize \frac{1}{2}}M_s. \] 実際,図に示した玄武岩試料の測定では \(M_{rs}\) は \(M_s\) のほぼ半分になっています.
参考文献:
- Dunlop, D. J., and O. Ozdemir, Rock Magnetism --- Fundamentals and frontiers ---, 573 pp., Cambridge University Press, Cambridge, 1997.