４-２ 地震波の伝播
弾性体の波動： 一般に地震の揺れは最初のカタカタという振動，続いて少し異質の振動，最後にユサユサという大きな振動の３段階からなります．これらは，それぞれP波，S波，表面波とよばれます．地震学では大地を弾性体とみなし，地震波をその中を伝搬する弾性波として解析します．以下に正確さは欠きますが，弾性体の波動の理論を簡単に説明します．
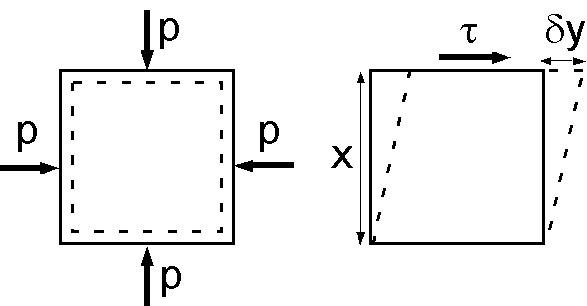
弾性体の一部が外力の作用で変形すると，その歪みが波動として伝わります．歪みには図のように２種類あり，１つ目は図左の圧力による体積歪み \(\Delta\) で， \(V\) と \(\rho\) を体積と密度として， \[ \Delta = \frac{-\delta V}{V} = \frac{\delta \rho}{\rho}, \] で定義されます． \(\Delta\) は体積の減少を正とし，無次元の量です．体積歪 \(\Delta\) と圧力 \(p\) には次のフックの法則が成り立ちます． \[ p = K\Delta. \] ここに，定数 \(K\) は体積弾性率（非圧縮率）で，値が大きいほど縮みにくい，または硬いといえます．
２つ目の歪みは図右のずれ歪み（せん断歪み） \(\epsilon\) で，弾性体の表面に沿ってずれ応力 \(\tau\) （せん断応力，応力とは単位面積当たりの力）を加えた場合の変形の程度を表わす無次元量で， \[ \epsilon = \frac{1}{2}\frac{\delta y}{x}, \] で定義されます．ずれ歪み \(\epsilon\) とずれ応力 \(\tau\) との間のフックの法則は次式となります． \[ \tau = 2\mu\epsilon. \] ここに，定数 \(\mu\) は剛性率で，値が大きいほどずれが生じにくくなります．
これらの体積歪み \(\Delta\) とずれ歪み \(\epsilon\) には次の波動方程式が成立します (１次元に単純化してあります)． \begin{eqnarray} \rho\frac{\partial^2\Delta}{\partial t^2} & = & \left(K+\frac{4}{3}\mu\right)\frac{\partial^2\Delta}{\partial x^2}, \label{eq01} \\ \rho\frac{\partial^2\epsilon}{\partial t^2} & = & \mu\frac{\partial^2\epsilon}{\partial x^2}. \label{eq02} \end{eqnarray} 式の導出は難解ですが，左辺と右辺はそれぞれ，ニュートンの運動方程式（\(ma=F\)）の \(ma\) と \(F\) に相当します．式 (1) の体積歪みによる波が縦波のP波で，式 (2) のずれ歪みによる波が横波のS波です．一般に \(\alpha\) を定数として，次の形の方程式は波動方程式とよばれます． \begin{equation} \frac{\partial^2\phi}{\partial t^2} = \alpha^2\frac{\partial^2\phi}{\partial x^2}. \label{eq03} \end{equation} 最も基本的な \(\phi\) の解は振幅を \(A\) として次式となります． \[ \phi = A\cos\kappa(x-\alpha t). \] これは速度 \(\alpha\) で伝搬する波で， \(\kappa\) は波数と呼ばれ波長 \(\lambda\) と \(\lambda=2\pi/\kappa\) の関係があります．式 (1) と (2) を (3) と比較することで，P波とS波の速度 \(v_P\) と \(v_S\) は， \begin{eqnarray} v_P & = & \sqrt{\frac{K+\frac{4}{3}\mu}{\rho}}, \label{eq04} \\ v_S & = & \sqrt{\frac{\mu}{\rho}}. \label{eq05} \end{eqnarray} となります．式 (4) と (5) を比較して，常にP波はS波より速いことが分かります．また，流体は剛性率 \(\mu\) がゼロですので，S波は流体の外核を伝わることはありません．
無限に広がる弾性体では，実体波と呼ばれるP波とS波だけが発生しますが，地表面のような表面がある場合は，表面に到達したP波とS波が複雑に干渉してレーリー波やラブ波と呼ばれる表面波が発生します．理論によると，表面波を表わす複雑な式には， \(z\) 軸を表面から深さ方向に取ると， \(e^{-kz}\) の形の項が含まれ，深さとともに減衰し表面付近のみの地震波であることが分かります．
地震波の反射と屈折： 地震波は水面の波と同様に，ホイヘンスの原理に基づいて，波線の方向に伝わる波面として扱うことができます．この原理によると，波面上の全ての点から球面状の素元波が発生しますが，これらは波線と直角方向には打ち消し合うので，各素元波に接する面が新しい波面となって進みます．下図（左）は波の屈折をホイヘンスの原理で示したもので，媒質２中の波の速度 \(v_2\) が媒質１の速度 \(v_1\) より速い場合です．媒質１を伝わってきた波面が図の AB を通り過ぎる時間を \(\Delta t\) とすると，点 A から発した素元波の半径は \(v_2\Delta t\) となり，幾何学から次の入射角 \(i\) と屈折角 \(f\) のスネルの法則が示されます． \begin{equation} \frac{\sin i}{v_1} = \frac{\sin f}{v_2}. \label{eq06} \end{equation}
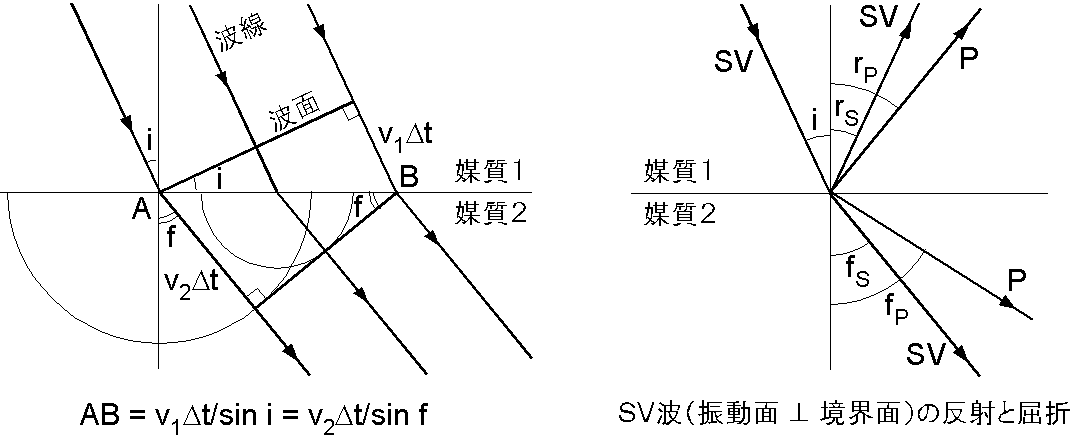
地震波の反射や屈折が光などの場合と異なるのは，P波が境界面に入射するとS波も発生し反射S波や屈折S波が生じることです．但し，発生するS波は横波としての振動方向が境界面に垂直な面内にある波です（SV波）．S波が入射する場合，振動方向が境界面に平行な波（SH波）はP波は発生せずに，反射SH波と屈折SH波となります．しかし，SV波が入射すると反射SV波と屈折SV波の他に反射P波と屈折P波が発生します．その様子を上図（右）に示しますが，地震波の速度は媒質２の方が媒質１よりも速いこと，また両媒質中でP波の方がS波よりも速いとして描いてあります．この場合にもホイヘンスの原理から，図のように角度を表記すると，スネルの公式は次のようになります．また，SV波の入射角と反射角は等しく， \(i=r_S\) です． \[ \frac{\sin i}{v_{S1}} = \frac{\sin r_S}{v_{S1}} = \frac{\sin r_P}{v_{P1}} = \frac{\sin f_S}{v_{S2}} = \frac{\sin f_P}{v_{P2}}. \]
スネルの法則 (6) によると， \(v_2\) > \(v_1\) の場合は屈折波は境界面の方へ曲げられ，ある入射角 \(i_c\) で屈折角が \(f\) = 90° となり波は媒質２に伝わりません．この現象を全反射といい，次式で決まる入射角 \(i_c\) を臨界角といいます． \begin{equation} \sin i_c = \frac{v_1}{v_2}. \label{eq07} \end{equation}
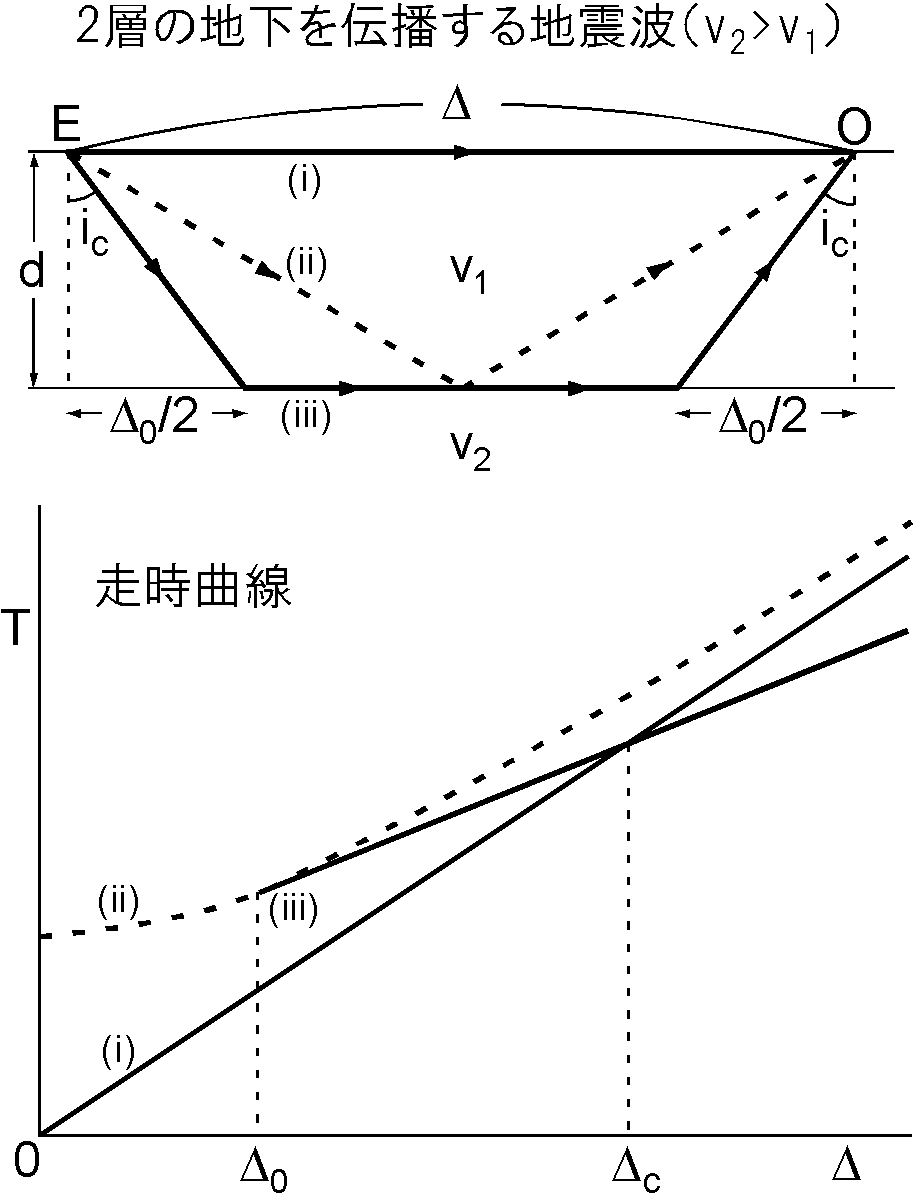
走時曲線： 地震波の伝わり方を右図（上）のような２層構造について考え， \(v_2\) > \(v_1\) とします．地震学では震源の真上の地表の点を震央，震央からの距離を震央距離といいます．いま，地震は震央 E で発生し，震央距離 \(\Delta\) の点 O でP波を観測するとします．観測される地震波は (i) 地表を伝わって来た直達波， (ii) 境界面で反射して来た反射波（図では点線で示す）， (iii) 境界面に臨界角 \(i_c\) で入射し，第２層の最上部を伝わり，再び臨界角 \(i_c\) で地表に到達した屈折波（臨界屈折波），の３通りです．これらの地震波の観測点への到達時間 \(T\) は， \(d\) を第１層の厚さとして，それぞれ以下のようになります． \begin{eqnarray*} T_1 & = & \Delta/v_1,\\ T_2 & = & \sqrt{\Delta^2 + 4d^2}/v_1, \\ T_3 & = & 2\frac{d/\cos i_c}{v_1} + \frac{\Delta - 2d\tan i_c}{v_2}, \\ & = & \frac{\Delta}{v_2} + \frac{2d}{v_1 v_2}\sqrt{v_2^2 - v_1^2}. \end{eqnarray*} 地震学では時間 \(T\) を走時といい，縦軸に走時 \(T\) を，横軸に震央距離 \(\Delta\) を取ったグラフを走時曲線といいます．図（下）に直達波，反射波（点線），屈折波の走時曲線を示します．震央距離が小さいときは直達波が先に到着します．屈折波は震央距離が \(\Delta_0=2d\tan i_c\) を超えてから現れますが，震央距離が大きくなると直達波よりも先に到達するようになります．反射波は常に最後に到達します（\(\Delta_0\)では屈折波と同時）．そのため，観測点に最初に到達するP波について走時曲線を描くと，ある震央距離 \(\Delta_c\) でグラフは折れ曲がります．震央距離が \(\Delta_c\) の地点では，直達波と屈折波が同時に到達します．そこで， \(\Delta=\Delta_c\) で \(T_1=T_3\) の条件から，次の第１層の厚さ \(d\) を与える式が得られます． \begin{equation} d = \frac{\Delta_c}{2}\sqrt{\frac{v_2 - v_1}{v_2 + v_1}}. \label{eq08} \end{equation} この原理に従い， 20世紀初頭に地殻とマントルの２層構造が発見され，境界面は発見者にちなんでモホロビチッチ不連続面（モホ面）とよばれます．
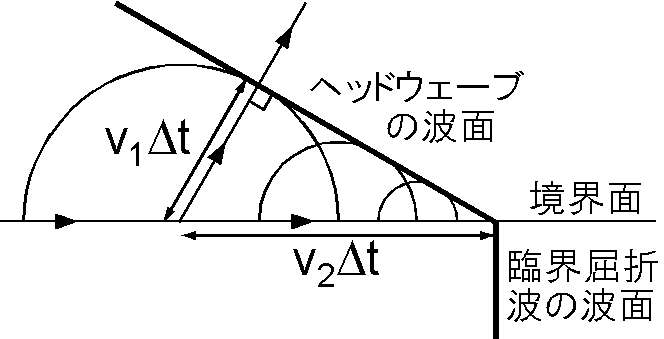
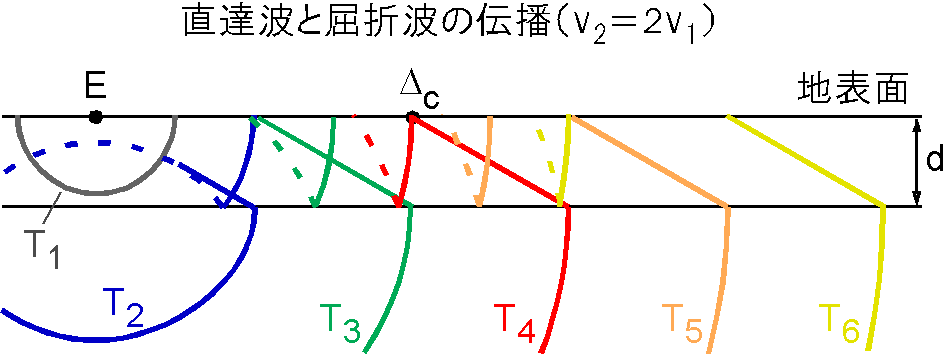
第２層最上部を伝わる地震波が地表へ戻る現象は，船の舳先から斜め後方に出る波と同じで，ヘッドウェーブといいます．波源が波の速度よりも速い速度で移動するときに発生します．右図はホイヘンスの原理によるヘッドウェーブの説明で，波面と境界面の角度の正弦が \(v_1/v_2\) となり，ヘッドウェーブは地表面に対して臨界角 \(i_c\) で入射することが分かります．下図は直達波や屈折波の波面が伝わる様子を， \(v_2\) が \(v_1\) の２倍として地震発生から一定時間毎に示します (点線は反射波)．時間が \(T_1\) では反射波も屈折波も発生していないこと， \(T_2\) では反射波と屈折波は地表に達していないこと， \(T_3\) では直達波が屈折波より先行していること， \(T_4\) では直達波と屈折波が同時に震央距離 \(\Delta_c\) に達していること， \(T_5\) と \(T_6\) では屈折波が直達波より先行していることが分かります．
走時曲線の解析を地球全体に拡大すると地球内部構造を決定できます．この場合の震央距離は地球中心から見た震央と観測点とのなす角度となります．震央距離が 103-143° の間でP波が観測されないことから核の存在が明らかになりました．さらに，震央距離が約 100° を越えるとS波が観測されないことから，地球核が流体であることが分かりました．但し，流体は外核のみで，固体の内核の存在はさらに詳しい観測から分かりました．このように，地震の観測により地球の構造が大きく地殻，マントル，核の３層からなり，さらにマントルは上部マントルと下部マントル，核は外核と内核からなることが明らかにされました．
さらに，地震波トモグラフィーとよばれる，医学のCTスキャンと似た原理により，地殻やマントル内の詳細な構造が解明されています．地球内のある部分の地震波速度が，その深さに対する標準の値からどれくらい速いか遅いか求めることで，マントルに沈み込むプレートなどが実際に観測されました．但し，あくまで観測量は地震波速度で，標準値からの数%以下の差という僅かな量です．地震波速度の速い部分は冷たくて固い部分（沈み込むプレートなど），遅い部分は軟らかくて熱い部分（火山地域，ホットスポット，プリューム，など）に相当すると解釈されます．
問題４-２-１
（１） \(k\) と \(\omega\) を正の定数として，位置 \(x\) と時間 \(t\) の次の関数は正弦波を表します． \[ \sin(kx - \omega t). \] 波長 \(\lambda\) と周期 \(T\) をそれぞれ \(k\) と \(\omega\) で表しなさい．
（２） 正弦波 \(\sin(kx - \omega t)\) と \(\sin(kx + \omega t)\) は，それぞれ \(x\) の正と負の方向へ伝わることを説明しなさい．また，波の速度を \(k\) と \(\omega\) で表しなさい．
（３） \(\sin(kx - \omega t)\) と \(\sin(kx + \omega t)\) が本文の式 (3) の波動方程式， \[ \partial^2\phi/\partial t^2 = \alpha^2\partial^2\phi/\partial x^2, \] の解であるための \(k\)， \(\omega\)， \(\alpha\) の関係を導き， \(\alpha\) が波の速度となっていることを示しなさい．
（４） 岩石の加圧実験から花崗岩の弾性定数と密度が次のように測定されたとします． \[ K=5.3\times 10^{10}\ \mathrm{Pa}, \quad \mu=3.1\times 10^{10}\ \mathrm{Pa}, \quad \rho=2650\ \mathrm{kg/m^3}. \] 但し， Pa （パスカル）は圧力の単位で [N/m2 = kg m-1 s-2] です．これらの値を本文の式 (4) と (5)， \[ v_P=\sqrt{(K+(4/3)\mu)/\rho}, \quad v_S=\sqrt{\mu/\rho}. \] に代入して花崗岩中を伝搬するP波およびS波の速度を求めなさい．
問題４-２-２
（１） 速度 \(v_1\) の波が速度 \(v_2\) の波となって反射する場合も，入射角 \(i\) と反射角 \(r\) について次のスネルの法則が成立します．これをホイヘンスの原理を用いて作図することで説明しなさい． \[ \frac{\sin i}{v_1} = \frac{\sin r}{v_2}. \]
（２） ２層の地下構造を考え，地震波速度が次の表のようになっているとします．
| 層名（状態） | P波 [km/s] | S波 [km/s] |
| 第１層（固体） | 6 | 3 |
| 第２層（固体） | 8 | 4 |
| 第２層（流体） | 3 | ー |
では，P波，SV波，SH波が第１層から第２層へ入射角 \(i\) = 20° で入射したときの反射波や屈折波について，それらの反射角と屈折角を計算し，波線を下図に書き入れなさい．
問題４-２-３
（１） 本文で示した，屈折波の震央距離 \(\Delta\) への到達時間 \(T_3\)， \[ T_3 = \frac{\Delta}{v_2} + \frac{2d}{v_1 v_2}\sqrt{v_2^2 - v_1^2}, \] を導きなさい．
（２） 本文の式 (8) の，走時曲線が折れ曲がる震央距離 \(\Delta_c\) から第１層の厚さ \(d\) を与える式， \[ d = \frac{\Delta_c}{2}\sqrt{\frac{v_2 - v_1}{v_2 + v_1}}, \] を， \(\Delta_c\) への直達波と屈折波の到達時間 \(T_1\) と \(T_3\) を等置することで導きなさい．
（３） 日本の中部地方で，爆破地震によるP波の走時曲線を測定したところ，走時曲線が折れ曲がる震央距離は \(\Delta_c\) = 179 km，走時は \(T\) = 31 s であった．震央から最も遠い観測点では， \(\Delta\) = 292 km， \(T\) = 45 s であった．日本列島の地殻の厚さを計算しなさい．