1-3 エネルギー保存則と運動量保存則
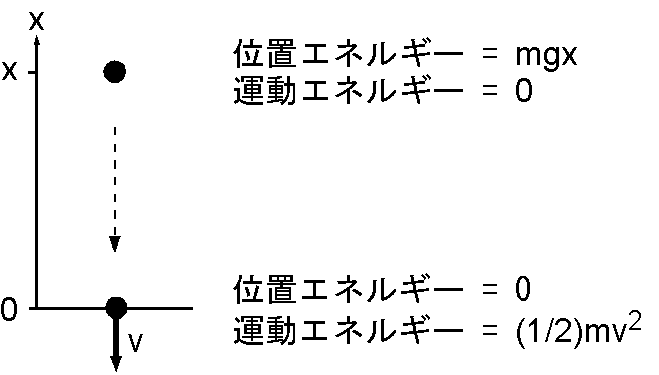
エネルギー保存の法則: 物体を地表からある高さまで持ち上げて離すと物体は勢い良く落下します.この様子を物理学では,位置のエネルギーが落下の際に運動エネルギーに変わると解釈します.物理学では,物体に力 \(F\) を加えて,その力の方向に \(s\) 動いたとき,力は \(Fs\) の仕事をしたと表現します.エネルギーとは仕事をすることのできる能力です.図で,質量 \(m\) の物体を地表(\(x = 0\))から重力 \(-mg\) に抗して高さ \(x\) まで持ち上げるときの仕事は \(mgx\) で,これが物体の位置エネルギー \(U\) です. \begin{equation} U = mgx. \label{eq01} \end{equation} 位置エネルギーは物体の落下とともに減少し,その分が運動エネルギー \(E\) へと変化します.運動エネルギーは速度 \(v\) を用いて次式で表されます. \begin{equation} E = {\scriptsize \frac{1}{2}}mv^2. \label{eq02} \end{equation} 運動エネルギーが式 (2) の表現になることは以下のようにして導かれます.ニュートンの運動方程式は, \[ m \frac{d^2x}{dt^2} = -mg. \] 両辺に \(dx/dt\) をかけて変形し,さらに \(t_0\) から \(t\) まで積分します. \begin{eqnarray*} m\frac{dx}{dt}\frac{d^2x}{dt^2} & = & -mg\frac{dx}{dt}, \\ \frac{1}{2}m\frac{d}{dt}\left[\left(\frac{dx}{dt}\right)^2\right] & = & -mg\frac{dx}{dt}, \\ \frac{1}{2}m\left[\left(\frac{dx}{dt}\right)^2\right]_{t_0}^t & = & -mg\int_{t_0}^t \frac{dx}{dt}dt. \end{eqnarray*} 時間 \(t_0 \rightarrow t\) で,物体の位置は \(x_0 \rightarrow x\),速度は \(v_0 \rightarrow v\) とすると, \[ {\scriptsize \frac{1}{2}}mv^2 - {\scriptsize \frac{1}{2}}mv_0^2 = -mg(x - x_0), \] となり,式 (2) による運動エネルギーの増加が位置エネルギーの減少に等しいことを表します(上図では, \(x_0=x,\ v_0=0\) から \(x=0,\ v=v\)).さらに次式のように変形すると,運動エネルギー \(E\) と位置エネルギー \(U\) の和が一定であることが分かります. \begin{equation} {\scriptsize \frac{1}{2}}mv^2 + mgx = {\scriptsize \frac{1}{2}}mv_0^2 + mgx_0. \label{eq03} \end{equation} この式を力学的エネルギー保存の法則といいます.
なお,重力加速度が一定と見なせない天体スケールでの物体の落下については問題1-3-2で考察します.天体スケールでも,式の表現は異なりますが力学的エネルギー保存則は成り立ち, → このページで解説しています.
運動量保存の法則: 質量 \(m\) の物体が速度 \(v\) で運動しているとき,運動の勢いを表すベクトル量を, \begin{equation} {\bf p} = m{\bf v}, \label{eq04} \end{equation} で表し,運動量といいます.質量 \(m_1\), \(m_2\) の2つの物体が互いに力を及ぼすが,外からの力(外力)が働かないときは,運動量の合計は保存されます.いま,物体1が物体2から受ける力を \({\bf F}_{1\Leftarrow2}\) などと表すとき,ニュートンの運動方程式より次の関係が成立します. \[ m_1 \frac{d{\bf v}_1}{dt} = {\bf F}_{1\Leftarrow2} , \qquad m_2 \frac{d{\bf v}_2}{dt} = {\bf F}_{2\Leftarrow1}. \] 両辺の和を取り,作用反作用の法則から, \({\bf F}_{1\Leftarrow2} + {\bf F}_{2\Leftarrow1} = 0\) ですので, \(m_1 d{\bf v}_1/dt + m_2 d{\bf v}_2/dt = 0\) となり,積分すると次のように一定となります(\(C\) は積分定数).この運動量保存則は多数の物体からなる系でも成立します. \begin{equation} m_1 {\bf v}_1 + m_2 {\bf v}_2 = C. \label{eq05} \end{equation}
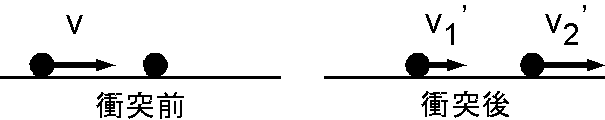
運動量保存則の応用例として,質量 \(m\) の物体1が速度 \(v\) で,静止している同じ質量の物体2に衝突する現象を考えます.運動は一直線上に限るとします.物体1と2の衝突後の速度を \(v_1^\prime\), \(v_2^\prime\) とすると,運動量保存の法則から, \[ m v = m v_1^\prime + m v_2^\prime, \] となります.力学的エネルギーが保存される場合は(弾性衝突), \[ (1/2) m v^2 = (1/2) m v_1^{\prime 2} + (1/2) m v_2^{\prime 2}. \] これらの2式を \(v_1^\prime\) と \(v_2^\prime\) について解くと, \[ v_1^\prime = 0 , \qquad v_2^\prime = v, \] となり,衝突後は物体1は静止し,物体2は物体1と同じ速度で動き出すことが分かります.
一般には衝突で力学的エネルギーは保存されずに熱エネルギーなどに変わります(非弾性衝突).衝突後に2つの物体が合体する場合には,その速度を \(v^\prime\) とすると,運動量保存則から, \[ m v = (m + m) v^\prime. \] よって, \(v^\prime = v/2\) となります.この場合,力学的エネルギー \(E\) は減少し, \[ \Delta E = (1/2) m v^2 - (1/2) (2m) (v/2)^2 = (1/4) m v^2, \] が熱エネルギーなどに変換されたことになります.
回転運動と角運動量:
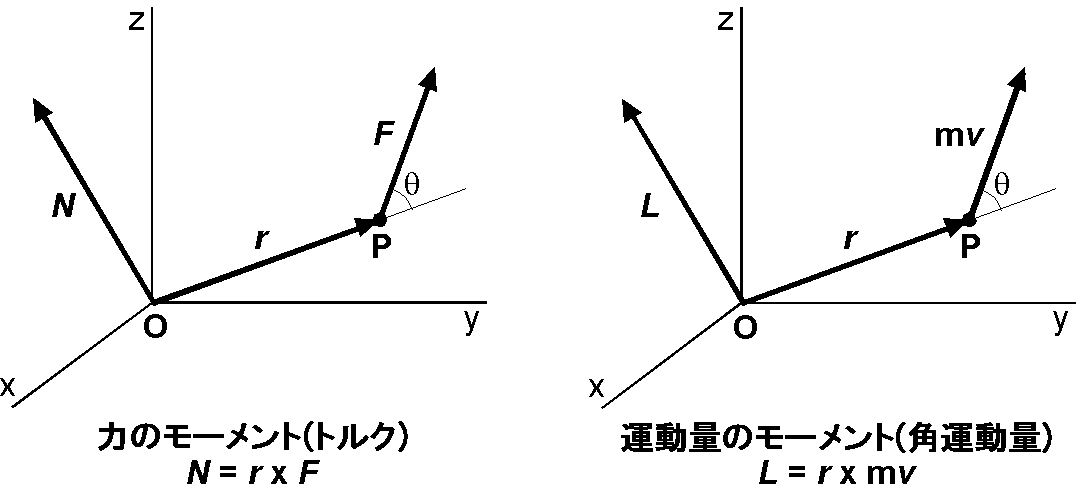
物体を中心 O の回りに回転させる能力を表す量を力のモーメント(トルク)といいます.上図(左)で,点 P に働く力 \(F\) のモーメント \(N\) は,てこの原理と同じですので, \(N=rF\sin \theta\) ですが,次のように \({\bf r}\) と \({\bf F}\) のベクトル積として表します. \begin{equation} {\bf N} = {\bf r}\times {\bf F}. \label{eq06} \end{equation} 一方,物体が中心 O の回りに回転するいきおいを表す量は,運動量 \(mv\) のモーメントで,これを角運動量 \(L\) といいます.上図(右)から, \(L=rmv\sin \theta\) で,次のベクトル積で表します. \begin{equation} {\bf L} = {\bf r}\times m{\bf v}. \label{eq07} \end{equation} ここで, \({\bf N}\) と \({\bf L}\) の関係を見てみます.簡単のために \({\bf r}\), \({\bf F}\), \({\bf v}\) は \(x\)-\(y\) 平面上にあるとすると, \({\bf N}\) も \({\bf L}\) も \(z\) 成分のみとなり,ベクトル積の公式から, \begin{eqnarray*} N & = & xF_y - yF_x, \\ L & = & xmv_y - ymv_x. \end{eqnarray*} \(L\) を時間 \(t\) で微分すると, \[ \frac{dL}{dt} = \frac{dx}{dt}mv_y + xm\frac{dv_y}{dt} - \frac{dy}{dt}mv_x - ym\frac{dv_x}{dt}. \] ここで,速度 \(v_x=dx/dt\),加速度 \(a_x=dv_x/dt\),運動方程式 \(ma_x=F_x\),などを考慮し整理すると, \[ dL/dt = xma_y - yma_x = xF_y - yF_x = N, \] となります.任意の方向の \({\bf r}\), \({\bf F}\), \({\bf v}\) についても同様の計算から,次の \({\bf L}\) と \({\bf N}\) の関係式を得ます. \begin{equation} \frac{d{\bf L}}{dt} = {\bf N}. \label{eq08} \end{equation} この式は,角運動量の時間増加率は回転させる力のモーメントに比例することを示します.
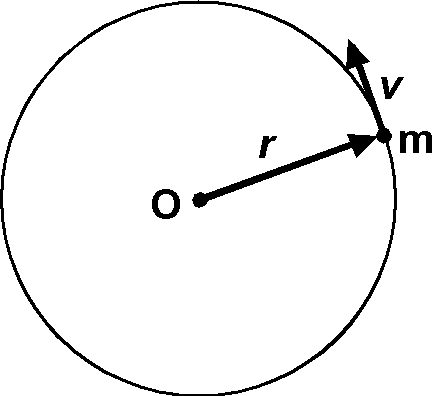
角運動量の例として,惑星の等速円運動による公転を考えます.惑星の質量を \(m\),軌道半径を \(r\),公転の角速度を \(\omega\) とすると,角運動量は, \[ L = rmv = rmr\omega = mr^2\omega, \] となり,角運動量は,質量,角速度,及び軌道半径の2乗に比例して大きくなります.また,等速円運動では \(r\) も \(\omega\) も一定ですので, \(L\) が一定となるのは明らかですが,楕円軌道の場合も \(L\) は一定値となります.その理由は,惑星が太陽から受ける引力 \({\bf F}\) は \({\bf r}\) と同一直線上で反対向きですので,式 (6) から \({\bf N}\) はゼロとなり,式 (8) から \({\bf L}\) の時間微分はゼロ,即ち角運動量は一定となります.これを角運動量保存の法則といい,万有引力のように力の作用線が常に原点を通る場合(中心力)に成立します.
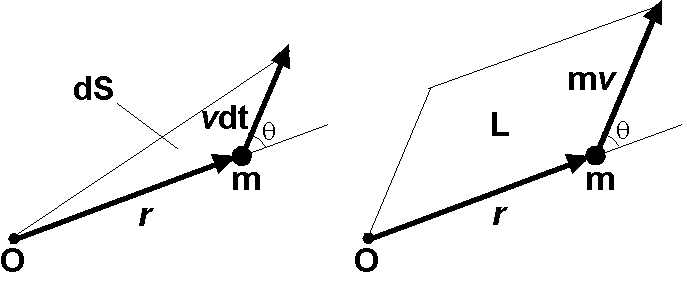
ケプラーの第2法則である面積速度一定の法則は角運動量保存則から導くことができます.微小時間 \(dt\) に惑星が描く面積は,図(左)の三角形の面積 \(dS=(1/2)rvdt\sin\theta\) で近似できます.一方,質量 \(m\) の惑星の角運動量は, \(L=rmv\sin\theta\) で,図(右)の平行四辺形の面積となります.よって, \[ \frac{dS}{dt} = \frac{rv\sin\theta}{2} = \frac{L}{2m}, \] となります.惑星に働く引力は中心力のため,右辺の \(L\) は一定,即ち面積速度 \(dS/dt\) は一定です.
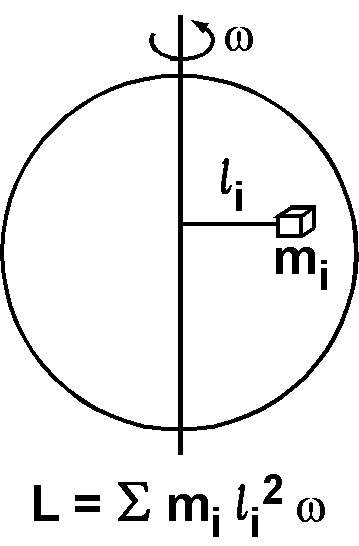
最後に,密度が一様な球が角速度 \(\omega\) で自転するときの角運動量について考えます.図のように,球の内部を多くの微小部分に分け, \(i\) 番目の部分の質量を \(m_i\), 回転軸からの垂直距離を \(l_i\) とします.この微小部分の角運動量は,上記の惑星の場合と同じように, \(m_i l_i^2 \omega\) ですので,これを足し合わせて,球の自転による角運動量は, \(L = \sum_i m_i l_i^2 \omega\) となりますが,この式に含まれる次の量を慣性モーメント \(I\) として定義します. \begin{equation} I = \sum_i m_i l_i^2. \label{eq09} \end{equation} 角運動量 \(L\) は慣性モーメント \(I\) と角速度 \(\omega\) により次式で表されます. \begin{equation} L = I \omega. \label{eq10} \end{equation}
また,球の自転による運動エネルギー \(E\) は,各微小部分の運動エネルギーの合計として求まります. \(i\) 番目の微小部分の運動エネルギー \((1/2)m_iv_i^2=(1/2)m_il_i^2\omega^2\) を合計して \((1/2)\sum_i m_i l_i^2 \omega^2\) となりますが,慣性モーメント \(I\) を用いて次式で表されます. \begin{equation} E = {\scriptsize \frac{1}{2}}I \omega^2. \label{eq11} \end{equation} 式 (10) と (11) は一般の剛体でも成立し,角運動量と回転のエネルギーは,式 (4) の質点の運動量, \(p=mv\),と式 (2) の運動エネルギー, \(E={1\over2}mv^2\),の質量 \(m\) と速度 \(v\) を,それぞれ慣性モーメント \(I\) と角速度 \(\omega\) で置き換えた形になっていることが分かります.
自転の運動でも,外力が働かない系では角運動量保存則が成立します.アイススケーターのスピンが良い例で,広げていた腕を縮めて慣性モーメント \(I\) を小さくすると,式 (10) の角運動量 \(L\) が一定のため,角速度 \(\omega\) が増加することになります.
問題1-3-1
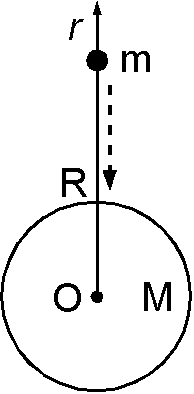
原始惑星の表面では,微小天体の落下により重力エネルギーが熱エネルギーとして解放されました.いま,質量 \(M\),半径 \(R\) の球に,質量 \(m\) の物体が遠方から落下する場合のエネルギーについて,図のように \(r\) 軸を取って考えます.
- (1) 球表面(\(r=R\))に位置する物体を,球の引力に抗して,無限遠(\(r=\infty\))まで運ぶに要する重力エネルギー \(U\) の式を導きなさい.
- (2) 無限遠で静止していた物体が落下して,球表面に衝突するときの速度 \(v\) の式を導きなさい.
- (3) 半径 2000 km,密度 5000 kg/m3 の原始惑星に質量 1 kg の物体が落下する場合の \(U\) と \(v\) を求めなさい.万有引力定数は G = 6.674×10−11 m3 kg−1 s−2 です.
- (4) 重力エネルギーが物体を加熱する熱エネルギーに変換されたとします.物体の比熱を \(c\) = 1000 J kg-1 K-1 とすると,物体の温度は何 K 上昇したか? 但し,物体の融解熱は考慮しないとします.
問題1-3-2
惑星の多くには磁場があり,磁場の発生は電気伝導性の流体核でのダイナモ作用によると考えられています.ダイナモ作用の原因の1つは自転によるコリオリ力(→ 3-4 自転とコリオリ力)ですので,磁場強度と自転の角運動量との相関が予想されます.これは,軌道半径のボーデの法則にちなんで,磁気的ボーデの法則とよばれています.
- (1) 地球と金星は質量も大きさも近い岩石惑星ですが,金星の磁場は地球の1万分の1以下です.この違いは,金星の極めて遅い自転速度が原因かもしれません.前問の (d) で導いた球の慣性モーメントの式を次のデータに適用して,地球と金星の自転の角運動量を計算し,地球の値との比を求めなさい.
惑星 半径 [km] 質量 [kg] 自転周期 [d] 地球 6371 5.974x10\(^{24}\) 0.9973 金星 6052 4.869x10\(^{24}\) 243.0 - (2) 惑星の磁場強度は,惑星中心に位置すると仮定した棒磁石の強さ,仮想的磁気双極子モーメント(VDM, virtual dipole moment)で表されます.地球の値で規格化した自転の角運動量 \(L\) と磁場強度 VDM を,太陽も含めて表に示します.上で得た金星の値を加えて,両対数グラフに角運動量(横軸)と磁場強度(縦軸)をプロットしなさい.(→ 両対数グラフ用紙)
(VDM の値は,惑星は, Ness, Phil. Trans. R. Soc. Lond. A., 349, 249, 1994.,太陽は, Tsuneta et al., Astrophys. J., 688, 1374, 2008.,に基づき推定しました.)
天体 太陽 水星 金星 地球 火星 木星 土星 天王星 海王星 \(L\) 1.6x10\(^8\) 1.4x10\(^{-4}\) 1 2.9x10\(^{-2}\) 9.6x10\(^4\) 1.9x10\(^4\) 3.2x10\(^2\) 3.8x10\(^2\) VDM 6.6x10\(^6\) 6.1x10\(^{-4}\) 5.6x10\(^{-5}\) 1 3.0x10\(^{-4}\) 2.0x10\(^4\) 5.9x10\(^2\) 48 27
問題1-3-3
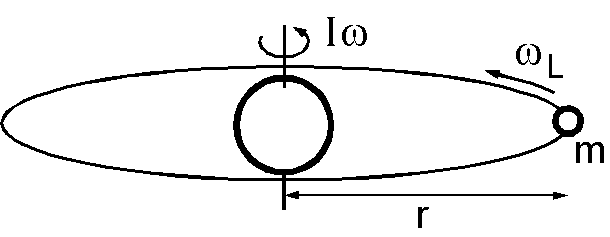
月は太陽系形成初期に地球に火星サイズの天体が衝突して形成されたとする巨大衝突説が有力です.当時は地球と月の距離は大変近く,地球の自転周期も短かったと考えられます.そこで当時の地球の自転周期を角運動量保存則から見積もってみます.地球-月系は厳密には共通重心の回りの運動ですが(→ 問題1-2-3を参照),ここでは簡略化して地球の自転の角運動量と月の公転の角運動量の和が保存されると仮定します.地球の慣性モーメントと自転の角速度を \(I\) と \(\omega\),月の質量,公転の角速度,軌道半径を \(m\), \(\omega_L\), \(r\) とします.地球-月系の角運動量の保存則は次式で表わされます. \[ I\omega + mr^2\omega_L = \mathrm{const.} \] また,月の公転角速度 \(\omega_L\) と軌道半径 \(r\) は → 問題1-2-2のケプラーの第3法則が成立します. \[ r^3\omega_L^2 = \mathrm{const.} \]
- (1) 月形成時の地球と月の角速度,月の軌道半径を \(\omega'\), \(\omega_L'\), \(r'\) とすると次式が成立します. \begin{eqnarray*} I\omega + mr^2\omega_L & = & I\omega' + mr'^2\omega_L', \\ r^3\omega_L^2 & = & r'^3\omega_L'^2. \end{eqnarray*} この2式から \(\omega_L'\) を消去して次の \(\omega'\) を求める式を導きなさい. \[ \omega' = \omega + \frac{mr^2\omega_L}{I}\left(1-\left(\frac{r'}{r}\right)^{1\over2}\right). \]
- (2) \(r'\) が 2 万km だったとして,この式から次の定数を用い,月形成時の地球の自転周期と月の公転周期を求めなさい. \begin{eqnarray*} I & = & (2/5)(5.97\times 10^{24})(6.37\times 10^6)^2 = 9.69\times 10^{37}\ \mathrm{m^2kg\quad (一様球を仮定)}, \\ m & = & 7.35\times 10^{22}\ \mathrm{kg}, \\ r & = & 3.84\times 10^8\ \mathrm{m\quad (38.4\ 万km)}, \\ \omega & = & 2\pi\div(0.997\times 24\times 3600) = 7.29\times 10^{-5}\ \mathrm{s^{-1}\quad (周期\ 0.997日)}, \\ \omega_L & = & 2\pi\div(27.3\times 24\times 3600) = 2.66\times 10^{-6}\ \mathrm{s^{-1}\quad (周期\ 27.3日)}. \end{eqnarray*}
- (3) 月は自転周期と公転周期が等しいですが,これは地球による潮汐摩擦で月の自転のエネルギーが散逸し自転速度が減少し,同じ面を常に地球に向ける力学的安定状態に達したためです(潮汐ロックや同期自転といいます).地球も月による潮汐作用で自転速度が減少しており,最後は常に同じ面を月に向けるようになるはずです.等しくなった地球自転と月公転の角速度を \(\omega'\),そのときの月軌道半径を \(r'\) とすると,次式が成立します. \begin{eqnarray*} I\omega + mr^2\omega_L & = & I\omega' + mr'^2\omega', \\ r^3\omega_L^2 & = & r'^3\omega'^2. \end{eqnarray*} この2式から \(\omega'\) を消去して次の \(r'/r\) についての方程式を導きなさい. \[ \left(\frac{r'}{r}\right)^{1\over2} = 1 + \frac{I\omega}{mr^2\omega_L} - \frac{I}{mr^2}\left(\frac{r'}{r}\right)^{-{3\over2}}. \]
- (4) この方程式は初等的には解けませんので逐次近似法を適用します.まず, (i) \(r'/r\) に適当な初期値を仮定して右辺を計算します.その値が左辺に等しいので,2乗して新たな \(r'/r\) とします. (ii) その \(r'/r\) を再び右辺に代入し次の段階の \(r'/r\) を求めます.この作業を繰り返し,値が収束するまで続けます.では,上記の定数を使用して逐次近似法を適用し,力学的安定状態に達した時点の月軌道半径と地球自転周期(月公転周期)を求めなさい.