1-2 運動方程式と万有引力
このページで使用する力学の基本的公式をまとめます.
ニュートンの運動方程式: 質量 \(m\) の物体に力 \({\bf F}\) が作用するとき,物体の加速度 \({\bf a}\) は物体に作用する力 \({\bf F}\) に比例し,物体の質量 \(m\) に反比例します.式で表すと, \[ {\bf F} = m {\bf a}. \]
万有引力の法則: 2つの物体に働く力 \({\bf F}\) の大きさは,物体の質量(\(m_1\) と \(m_2\))の積に比例し,物体間の距離 \(r\) の2乗に反比例します.式で表すと, \[ F = G \frac{m_1 m_2}{r^2}. \] ここに, \(G\) = 6.674\(\times\)10\(^{-11}\) m\(^3\) kg\(^{-1}\) s\(^{-2}\) は万有引力定数です.
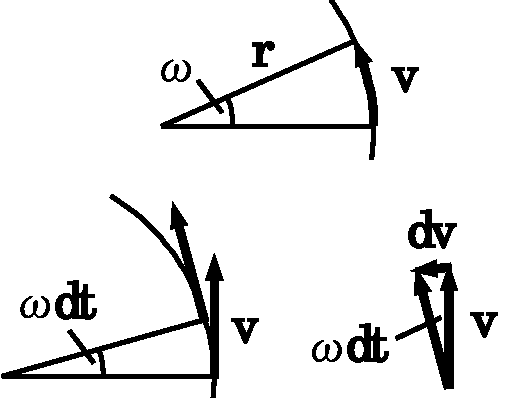
等速円運動による加速度: 角速度 \(\omega\) とは,角度 \(\theta\) が単位時間に増える割合で, \(\omega = d\theta/dt\) で表されます.右図(上)のように,半径 \(r\) の円運動では,単位時間に角度は \(\omega\) 増加し,その時の円弧の長さは速度 \(v\) となるので, \[ v = r \omega, \] となります.また,微小時間 \(dt\) の間に速度ベクトルの向きが \(\omega dt\) だけ変わるので,右図(下)から \(dv = v \omega dt\) となります.よって,物体に働く加速度 \({\bf a}\) の大きさは \(a=dv/dt=v\omega\) で表され,上の式を代入して, \[ a = r\omega^2 = \frac{v^2}{r}, \] となります. \(dv\) の向きは \(v\) に垂直ですので,等速円運動では中心に向かって加速度が働き,これを向心加速度,この加速度による力を向心力といいます.
問題1-2-1
重い荷車を一定の力で押し続けると,初めはゆっくり動き出し,その後は徐々に速度が上がります.即ち,力の作用で荷車に加速度を生じます.また,荷物が重いほど速度の上昇はゆっくりで,加速度が質量に逆比例しているというニュートンの運動方程式を体験できます.
しかし,これは地球上の物体が質量の大小に関わらず同時に落下する事実と矛盾するように思えます.地球上の全ての物体は同じ加速度 \(g\) (重力加速度)を地球から受けることを,ニュートンの運動方程式と万有引力の法則を用いて説明しなさい.但し,物体が地球から受ける引力は,地球中心に位置し,地球の全質量が集中した質点による引力と同等であるとします(地球が一様構造の球の場合に成立します).
問題1-2-2
質量 \(m\) の惑星が質量 \(M\) の太陽の回りを半径 \(r\) で等速円運動しているとして,公転周期の2乗が軌道半径の3乗に比例するという,ケプラーの第3法則を導きなさい.但し,惑星も太陽も質点とみなします.
問題1-2-3
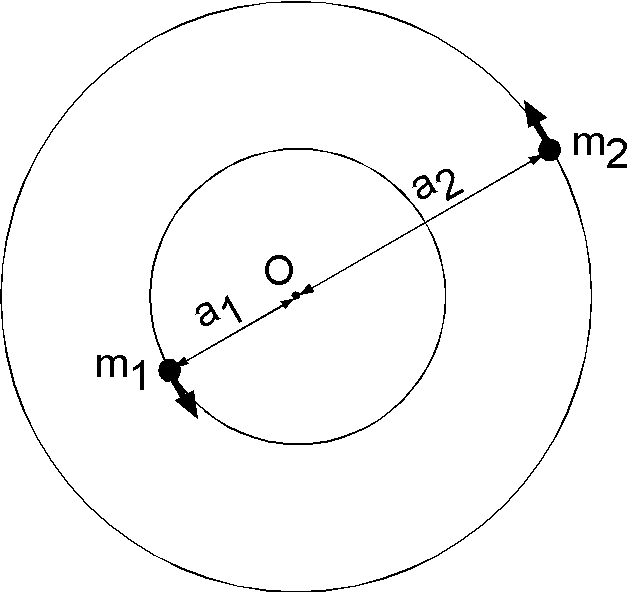
2つの恒星がそれらの重心の回りを軌道運動している天体を連星といいます.実際の軌道は楕円ですが,ここでは図のように円軌道の連星を考えます.この連星系では,質量 \(m_1\) の主星と質量 \(m_2\) の伴星が,系の重心 O の回りを互いに回っていて,主星と伴星はそれぞれ半径 \(a_1\) と \(a_2\) の円軌道を, O に対して反対方向の位置を保ちつつ,同じ角速度 \(\omega\) で等速円運動しているとします.
いま,両星の距離を \(a=a_1+a_2\),円運動の周期を \(T\) とします.それぞれの星について,遠心力と万有引力を等しいと置き,連星系について次式が成り立つことを示しなさい. \[ \frac{a^3}{T^2} = \frac{G}{4 \pi^2} (m_1 + m_2) \] この式は一般化されたケプラーの第3法則と呼ばれています.