1-4 太陽放射と地球表面温度
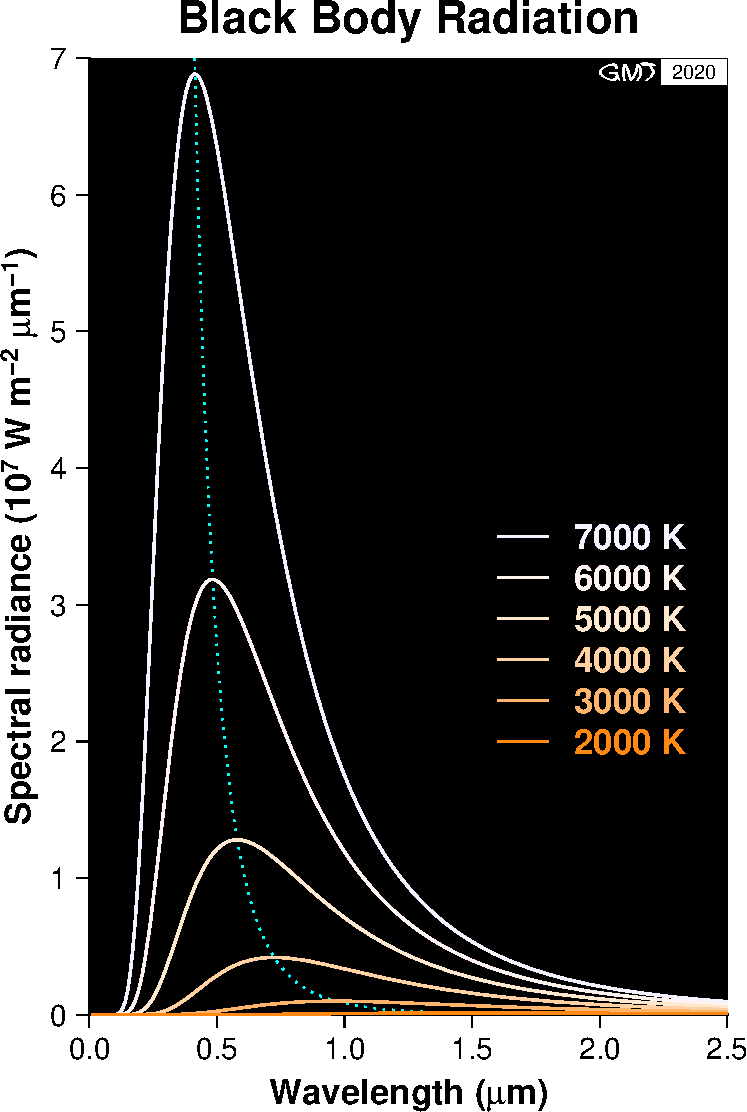
黒体放射の理論: 全ての電磁波を吸収する理論上の物体を黒体といいいます.黒体はその温度に応じて光や赤外線などの電磁波によるエネルギーを,プランクの法則に従って放射します.その際,黒体の温度 \(T\)(単位は K)と最も強度が強くなる電磁波のピークの波長 \(\lambda_m\)(単位は μm)には次の関係が成立し,ウィーンの変位則とよばれます. \[ \lambda_m T = 2900. \] 右図は,プランクの法則により放射されるエネルギーを,電磁波の波長の関数として異なる温度で表したグラフです.温度が高くなるほど急激に放射エネルギーが大きくなり,そのピークが短波長へシフトすることが分かります.
一方,右図の温度 \(T\) のグラフを全ての波長について積分すると,温度 \(T\) での黒体表面から単位面積当たり毎秒放射されるエネルギー \(E\)(単位は W/m2)となり,次のシュテファン・ボルツマンの法則とよばれます. \[ E = \sigma T^4. \] ここに, \(\sigma\) = 5.67×10-8 W m-2 K-4 はシュテファン・ボルツマン定数です.
全ての物体は近似的に黒体放射の理論に従ってエネルギーを放射します.太陽のような恒星では,エネルギーは主に光として放射され,表面温度の高い恒星ほどピークスペクトルの波長が短く,青白い光を放ちます.因みに,太陽は 6000 K の黒体に近く,エネルギーのピークは約 0.5 μm で,青〜緑となります.しかし,太陽光は全ての波長を含んだ連続光ですので,橙〜黃がかった白色を呈することになります.また,地球もエネルギーを宇宙へ放射しており,それは赤外線領域の電磁波によります.
太陽放射エネルギーと地球の表面温度: 地球軌道上で 1 m2 当たりの太陽放射エネルギーを太陽定数 \(S\) といい,観測値は 1366 W/m2 です.しかし,地球表面上の平均の太陽放射エネルギーは,球の断面積で受けたエネルギーを球の表面積で平均して4分の1の 341.5 W/m2 に減少します.さらに,地球のアルベド(反射能)が約 0.3 ですので,入射エネルギーのおよそ 30% が宇宙空間に反射され,平均の入射エネルギーは 235 W/m2 となります.
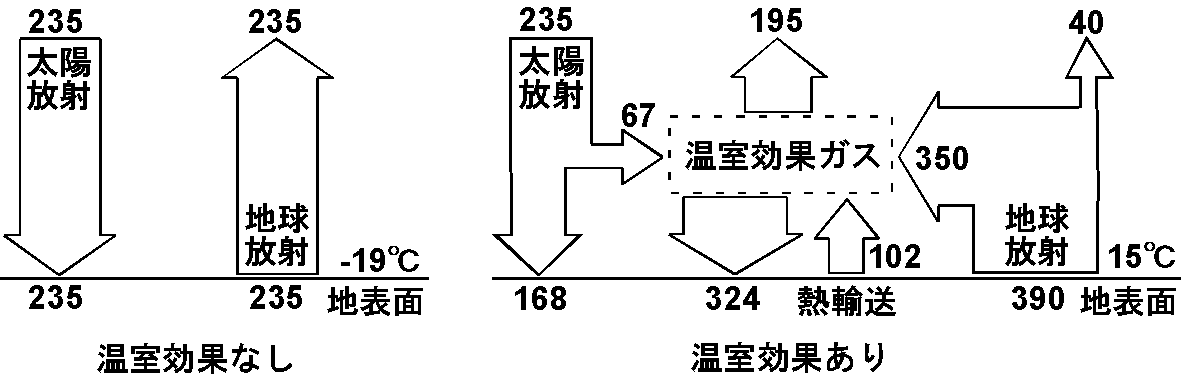
地球表面温度を一定に保つには,太陽放射による入射エネルギーと同量のエネルギーが宇宙空間に放射される必要があります.大気のような温室効果ガスがない場合は,左図のように地球表面からの放射エネルギーが入射エネルギーと同じ 235 W/m2 となり,シュテファン・ボルツマンの法則から地球の表面温度は -19 °C となります(図の数字の単位は W/m2).
実際の地球の平均表面温度が 15 °C に保たれているのは大気の温室効果のためです.地球表面温度 15 °C は,地球表面からの放射エネルギー 390 W/m2 に相当します.右図のように,温室効果ガスはこの地球放射の大部分と太陽放射の一部を一旦吸収しますが,吸収したエネルギーをあらゆる方向に再射出するので,地表面を暖めることになります.結局,温室効果により地表で 492 W/m2 のエネルギーが出入りするこになります.しかし宇宙から大気の上面を見ると,温室効果ガスがない場合と同じ 235 W/m2 のエネルギー収支であることに注意する必要があります.
地球の温室効果ガス: 大気の 99% を占める窒素と酸素にはほとんど温室効果はありません.主要な温室効果ガスは,温室効果への寄与率の多い順に,水蒸気(60%),二酸化炭素(26%),オゾン(8%),その他(6%)となります(値は研究結果により多少異なります).ここで重要な事実は,水蒸気の温室効果が最も大きいことです.しかし,この事実から二酸化炭素の排出は地球温暖化にはほとんど寄与しないと結論するのは誤りです.理由は,水蒸気の含有量は地表の温度により2次的に決まり,大気中に長期に留まることはないからです.例えば,大気の水蒸気含有量を 0% や 100% に設定しても, 14 日で 90% 回復し, 50 日で 99% 回復するという研究結果があります.これに対して,二酸化炭素などの温室効果ガスは数十年~百年というスケールで大気中に留まるので,地球温暖化に寄与することになります.
問題1-4-1
太陽放射のエネルギー源は太陽中心部での水素の核融合反応で,太陽は誕生後 46 億年間輝き続けています.しかし,放射性元素や核分裂などが発見されていなかった 19 世紀中頃は,考え得る最大のエネルギー源は原始太陽形成時の重力エネルギーでした.ヘルムホルツはこの重力収縮による全エネルギーを計算し地球で受ける単位時間あたりの太陽放射エネルギーで除することで,太陽の年令を2千万年としました.続いてケルビンもヘルムホルツの方法で太陽の年令を推定し,内部の密度分布の違いで2~6千万年となりました.この数千万年という値はケルビンの熱伝導理論による地球の年令と良く合い(この→ページと→問題を参照),ケルビンは信頼度の高い結果と考えたようです.そこで,ここでは密度一定の条件で太陽の誕生で生じた重力エネルギーを求め,太陽の年令を見積もってみます.
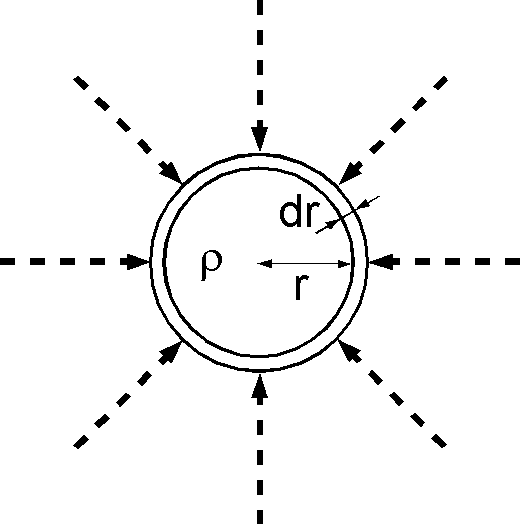
- (1) 重力収縮のエネルギーとは物質が無限遠から落下して集積するときの重力エネルギー \(U\) です.半径 \(r\) まで成長した質量 \(M_r\) の原始太陽に無限遠から質量 \(dm\) の物質が集積するときの重力エネルギーの増分 \(dU\) は \(G\) を万有引力定数として,→ 問題1-3-2(1)の式から, \[ dU = \frac{GM_rdm}{r}, \] となります.但し, \(M_r\) と \(dm\) は物質の密度を \(\rho\) として \[ M_r = 4\pi r^3\rho/3, \quad dm = 4\pi r^2\rho dr, \] と表わされます.では,重力収縮が終了後の太陽の半径と質量を \(R\) と \(M\) とするとき, \(dU\) を \(r\) で 0 から \(R\) まで積分して \(U\) を与える次式を導きなさい. \[ U = \frac{3}{5}\frac{GM^2}{R}. \]
- (2) 万有引力定数を G = 6.674×10−11 m3 kg−1 s−2,太陽半径を 6.96×105 km,密度を 1410 kg/m3 として重力エネルギーを計算し,太陽定数を 1370 W/m2,地球軌道半径を 1.50×108 km として太陽の年令を求めなさい.
問題1-4-2
ウィーンの変位則とシュテファン・ボルツマンの法則を用いて,太陽の表面温度や放射エネルギーに関する以下の問いに答えなさい.
- (1) 太陽のスペクトルは,ピークが波長 \(\lambda_m\) = 0.5 μm にあります.太陽の表面温度 \(T\) は何 K か?
- (2) 天文学では天体の全表面から毎秒放射されるエネルギーをその天体の光度といい,単位はワット(W)です(光源の放射強度をカンデラ(cd)で表わす光度とは別です).では,太陽光度 \(L\) を太陽定数 \(S\) と地球の軌道半径 \(a\) を用いて表しなさい.また, \(S\) を 1370 W/m2, \(a\) を 1.5×108 km として \(L\) を求めなさい.
- (3) 太陽光度 \(L\) と表面温度 \(T\) から太陽の半径 \(R\) を求める式を導き,値を計算しなさい.
問題1-4-3
氷期-間氷期の繰り返しなどの気候変動の主な原因はミランコビッチサイクルと考えられています.これは地球軌道要素の変動による北半球高緯度の夏の太陽放射の増減が気候変動に影響するという理論です.この理論では地球軌道の3要素の変動が地表の年平均太陽放射に影響すると考えます.その3要素とは公転軌道の離心率,自転軸の傾角,自転軸の歳差運動です.このうち,公転軌道の離心率 (\(e\)) が,地球が受ける太陽放射の年平均値に及ぼす影響の基本原理は比較的単純ですのでここで考察します.
太陽を焦点とする長半径 \(a\) の楕円軌道を, \[ r = \frac{a(1-e^2)}{1+e\cos\theta} \] で表わします.地球の受ける入射エネルギー \(I\) は \(r^2\) に反比例するので,地球と太陽の距離が \(r\) のとき, \[ I = k\left(\frac{r_0}{r}\right)^2 \] と表わせます.但し,\(k\) は太陽定数(一定と仮定)で決まる比例定数,\(r_0\) は 1 au の距離です.地球が受ける太陽放射の年平均値 \(\bar I\) は \(I\) を時間 \(t\) で 0 から周期 \(T\) まで積分し,次式で得られます. \begin{equation} \bar I = \frac{1}{T}\int_0^T I\,dt = \frac{kr_0^2}{T}\int_0^T\frac{1}{r^2}dt. \label{eq01} \end{equation}
- (1) ケプラーの法則による面積速度一定の式, \[ \frac{1}{2}r^2\frac{d\theta}{dt} = \mathrm{const.} \] を楕円の面積 \(\pi ab\) を周期 \(T\) で除した式と等置して次の関係式, \[ dt = \frac{T}{2\pi a^2\sqrt{1-e^2}}r^2 d\theta \] を示し,式 \eqref{eq01} の積分を \(\theta\) に変数変換して次の \(\bar I\) を与える式を導きなさい. \[ \bar I = k\left(\frac{r_0}{a}\right)^2\frac{1}{\sqrt{1-e^2}}. \]
- (2) 離心率 \(e\) は 0 と 0.06 の間で変動します(現在0.0167).長半径 \(a\) は一定とし,\(e\) が 0 と 0.06 の場合では太陽放射の年平均値は何%異なるか?