5-1 地温勾配と地殻熱流量
地下の温度は地表付近では 20〜30 °C/km の割合で増加し,これを地温勾配といいます.このことは地球内部からの熱の流れ,地殻熱流量,の存在を示します.エネルギーの流れである地殻熱流量の平均値は大陸地域では 65 mW/m2(mW はミリワット),海洋地域では 101 mW/m2,地球全体では 87 mW/m2 です.これらの値は,太陽から届くエネルギーを表わす太陽定数の 1366 W/m2 に比べて桁違いに小さいです.しかし,地球内部からの熱は多くの地質現象の原因となります.そのため,地殻熱流量を地球上の色々な地域で測定することで,地球内部の熱と温度の状態が分かり,プレートテクトニクスやマントル対流などの地球ダイナミクスについて,熱と温度という観点からの知見が得られます.
熱伝導の法則: 熱の輸送には伝導,対流,輻射がありますが,地殻やマントル上部では熱伝導によると考えられています.熱伝導は次のフーリエの熱伝導の法則で表わされます. \begin{equation} q = -k \frac{dT}{dx}. \label{eq01} \end{equation} ここに, \(q\) は座標 \(x\) 軸に沿った熱流量で, \(k\) と \(dT/dx\) は熱伝導度と温度勾配です.式中の負記号は熱は温度の高い部分から低い部分へ伝わるからです.
地殻熱流量は式 (1) に従って,地温勾配に岩石の熱伝導度を掛けることで見積もります.地温勾配は,大陸上では深井戸における温度測定から,海底では堆積物に刺した槍状のプローブの温度測定から決定します.岩石の熱伝導度は採取した岩石試料について実験室で測定します(海底では,プローブ内のヒーターを利用した直接測定もあります).例えば,地温が地表で 20 °C,深さ 1 km で 40 °Cで,岩石の熱伝導度は 3 W/m K(K は温度の単位のケルビン)とします. \(x\) 軸を深さ方向に取り, \(dT/dx\) = (40-20)/1000 を式 (1) に代入して, \(q\) = -60 mW/m2 となります.これは負の値ですので熱の流れは上向きです.
熱境界層としての地殻とマントル上層部: 地表付近の地温勾配 20〜30 °C/km を,例えば深さ 2000 km の下部マントル内部まで適用すると,温度は 40000〜60000 °C という非現実的な高温となります.このことは熱伝導による熱の輸送は地球上層部だけで,マントルや核では熱対流によることを示します.マントルは固体の岩石ですが地質学的時間スケールでは対流すると考えられます.熱対流による熱輸送の効率は高く,地温勾配は断熱温度勾配の 0.3〜0.5 °C/km 程度と推定されています.地表から熱対流による領域までの温度勾配の大きい部分は熱境界層といわれます.この熱伝導で熱を輸送する熱境界層としての地殻とマントル上層部をリソスフェアとよび,地質学的時間スケールでも固いプレートとして振舞います.リソスフェアの下は,より温度が高く軟らかいアセノスフェアとよばれる領域です.リソスフェアの厚さは海洋地域で 5〜100 km 程度,大陸地域で 150〜200 km 程度と考えられています.なお,リソスフェアとプレートは地球上層部の同じ部分を指す用語ですが,後者は前者をブロックとして分け(太平洋プレートなど),それらの間の衝突や沈み込みなどの造構運動を論ずる場合に使用するようです.
地球内部には,地温勾配の大きい熱境界層が他にも存在します.核と境界をなすマントル最下部は熱境界層と考えられ, D" 層とよばれています.また,マントルは深さ 660 km で上部マントルと下部マントルに2分されますが,それぞれが別個に対流する2層対流とマントル全体で対流する全マントル対流という異なる説があります.前者の場合には,上部と下部の境界では地温勾配の大きな熱境界層が形成されると考えられます.
地球内部の熱源の一つとして,放射性元素による発熱が考えられます.大陸地域では,上部地殻が放射性元素の熱源を多く含む花崗岩ですので,上層部ほど放射性元素の多い熱伝導のモデルで熱流量や温度分布を大体説明できます.海洋地域では,玄武岩の地殻とかんらん岩のマントルの放射性元素の含有量は,それぞれ花崗岩の十分の1と百分の1程度ですので,当初は海洋の熱流量は大陸よりも少ないと予想されていました.しかし,実際はむしろ海洋地域の方が熱流量が多いことが判明しました.この矛盾は,海嶺に上昇してきた高温のマントル物質が,海底で冷却される際のリソスフェア内の熱伝導で説明されました.さらに,海洋底拡大のために海洋リソスフェアは海嶺から離れるにつれて冷えて重くなり,アイソスタシーの結果として海底が深くなることも説明されました.
もう一つの地球内部の熱源としては,地球誕生時に地球内部に閉じ込められた熱があり,誕生後 46 億年経た現在でも地球は冷却の途中にあることは確かです.この熱源と放射性元素の熱源との割合については諸説ありますが,現在では半々程度と考えられています.
問題5-1-1
地球全体の地殻熱流量により地球内部から放出されるエネルギーを,地震活動や火山噴火により放出されるエネルギーと比較してみます.地震や火山により1年当り平均して放出されるエネルギーの推定値を,個々の地震や噴火の例とともに下表に示します(早川 1996).地震や火山のエネルギーが随分と大きいことは,例えば1トンの火薬爆発のエネルギーの約 4×109 J(TNT換算 - Wikipedia)と比較することで理解できます.
| マグニチュード5の地震 | 2×1012 J | 中級の火山噴火 | 1.5×1018 J |
| マグニチュード9の地震 | 2×1018 J | 最大級の火山噴火 | 1.5×1021 J |
| 地球全体の地震活動 | 4×1017 J/yr | 地球全体の火山活動 | 2×1019 J/yr |
(1) 地殻熱流量により地球の全表面から放出される1年当たりのエネルギーを,平均の地殻熱流量を 87 mW/m2 として計算しなさい.地球の半径を 6400 km とします.
(2) この地殻熱流量により放出されるエネルギーが地球の温度が冷却することにより補われていると仮定すると,地球が1 °C 冷却するのに何年かかるか?地球の質量を 6.0×1024 kg,平均の比熱を 1000 J/kg K とします.
問題5-1-2
地球内部の発熱源となる放射性元素を含む主要な元素はウラン(238U と 235U),トリウム(232Th),カリウム(40K)です.これらの元素の岩石中の含有率は岩石の種類や産地によって大きく異なります.ここでは,一測定例に基づいて岩石の発熱量を計算します.
(1) 放射性元素は放射性崩壊により時間とともに減少しますが,次表は放射性同位体の存在度と単位質量当たりの発熱量の現在値です(Turcotte & Schubert 2002, Table 4.2 より).ウラン元素としての発熱量とカリウム元素としての発熱量を,放射性同位体の存在度をそれぞれの発熱量に掛けることで,計算しなさい.
| 同位体 | 存在度 [%] | 発熱量 [W/kg] |
|---|---|---|
| 238U | 99.28 | 9.46×10-5 |
| 235U | 0.71 | 5.69×10-4 |
| 232Th | 100 | 2.64×10-5 |
| 40K | 0.0119 | 2.92×10-5 |
(2) 岩石中の U, Th, K の含有量の測定例を3種の岩石について次表に示します(Fowler 2005, Table 7.1 より).各岩石の単位質量当たりの発熱量 [W/kg] を計算しなさい.但し, U と K については (1) で求めた値を, Th については (1) の表の値を使用します.なお, ppm(perts per million)は百万分率です.また,表に含めた岩石密度を用いて,各岩石の単位体積当たりの発熱量 [W/m3] も計算しなさい.
| 岩石 | U [ppm] | Th [ppm] | K [%] | 密度 [kg/m3] |
|---|---|---|---|---|
| 花崗岩 | 4 | 15 | 3.5 | 2700 |
| 玄武岩 | 0.1 | 0.4 | 0.2 | 2900 |
| かんらん岩 | 0.006 | 0.04 | 0.01 | 3200 |
問題5-1-3
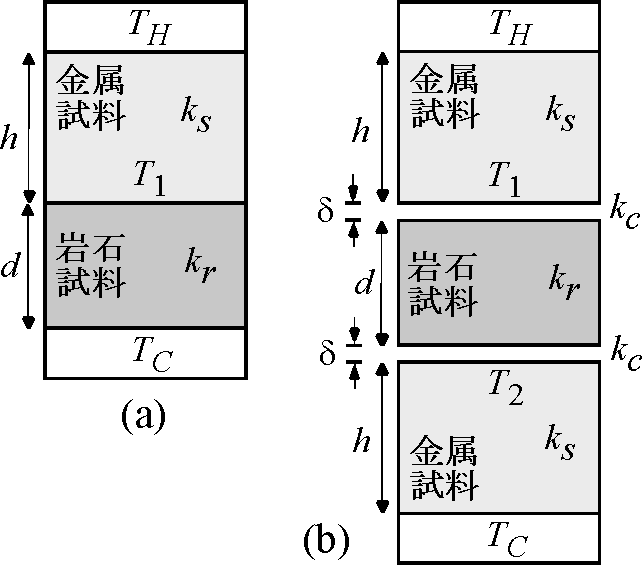
岩石の熱伝導度を標準試料と比較して測定する方法を右図に示します.図 (a) は最も簡単な方法で,熱伝導度 \(k_r\),厚さ \(d\) の岩石試料の上に厚さ \(h\) の標準試料を重ね,上下の高温槽と低温槽の温度をそれぞれ \(T_H\) と \(T_C\) に保ちます.標準試料には熱伝導度 \(k_s\) が既知の銅などの金属棒を使用し,岩石試料と金属試料の境界面で測定した温度を \(T_1\) とします.金属試料を流れる熱流量 \(q\) は \(q=k_s(T_H - T_1)/h\) です.これと同じ熱流量が岩石試料を流れるので,岩石の熱伝導度 \(k_r\) は \(k_r=qd/(T_1 - T_C)\) として決定できます.
しかし,この方法の欠点は岩石試料と金属試料の境界面の熱抵抗(主に空気の層が原因)により誤差が生じることです.そこで,図 (b) のように同じ厚さの金属試料を岩石試料の上下に配置します.上側の金属試料の底面の温度を \(T_1\),下側の金属試料の上面の温度を \(T_2\) とします.境界面の厚さと熱伝導度を \(\delta\) と \(k_c\) とし,2つの境界面で同じ値とします.金属試料中の熱流量は,\(q=k_s(T_H - T_1)/h\) または \(q=k_s(T_2 - T_C)/h\) として決定します.これと同じ熱流量 \(q\) が岩石試料と境界面を流れるので次式が成立します. \[ \frac{T_1-T_2}{q} = \frac{d}{k_r} + \frac{2\delta}{k_c}. \]
(1) この式を導きなさい.
(2) 岩石の熱伝導度 \(k_r\) をこの式を利用して測定する方法を考案しなさい.但し,\(\delta\) と \(k_c\) は常に同じ値とします.
参考文献:
- Fowler, C.M.R., The Solid Earth: An Introduction to Global Geophysics (Second Edition), 685 pp., Cambridge University Press, 2005.
- 早川由紀夫,2部 火山 (p.93-179),新版地学教育講座2 地震と火山, 191 pp.,東海大学出版会,東京, 1996.
- TNT換算 - Wikipedia, URL:https://ja.wikipedia.org/wiki/TNT換算
- Turcotte, D. & G. Schubert, Geodynamics (Second Edition), 456 pp., Cambridge University Press, 2002.