問題1-2-2 解説
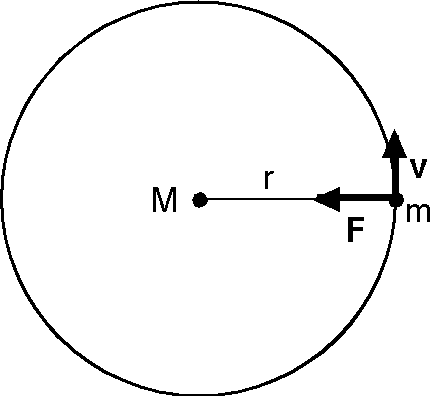
図のように,質量 \(M\) の太陽と質量 \(m\) の惑星の間には万有引力 \(F\) が働きますが,この力が速度 \(v\) で等速円運動する惑星に働く向心力となっています. \[ F = G\frac{Mm}{r^2} = mr\omega^2. \] よって, \[ \frac{1}{r^3\omega^2} = \frac{1}{GM}. \] 公転の角速度 \(\omega\) と公転周期 \(T\) の関係, \[ \omega = \frac{2\pi}{T}, \] を代入して整理すると, \[ \frac{T^2}{r^3} = \frac{4\pi^2}{GM}. \] これは万有引力定数と太陽の質量だけで決まる一定値で,ケプラーの第3法則が導かれました.
ここで,惑星として地球を考え,得られた式の \(r\) には地球の平均軌道半径(1 au(天文単位) = 約 1 億 4960 万km)を, \(T\) には 1 恒星年(約 365.26 日)を代入して太陽の質量を見積もってみます.
- \(G\) = 6.674\(\times\)10\(^{-11}\) m\(^3\) kg\(^{-1}\) s\(^{-2}\)
- \(r\) = 1.496\(\times\)10\(^{11}\) m
- \(T\) = 365.26\(\times\)24\(\times\)3600 = 3.156\(\times\)10\(^7\) s
を代入して計算すると, \[ M = 1.988\times 10^{30}\ \mathrm{kg}, \] という値となります.実際の地球の公転軌道は楕円ですが,円軌道による簡単な計算でも,天文学で採用されている太陽質量 1.9891\(\times\)10\(^{30}\) kg とほぼ同じ結果が得られました.