問題1−3−1 解答
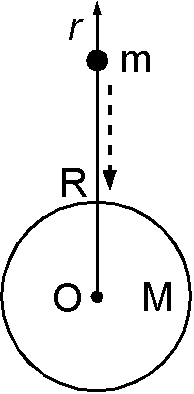
(1) 万有引力に抗する力は, \(GMm/r^2\) ですので,これを \(r=R\) から \(r=\infty\) まで積分して, \begin{eqnarray*} U & = & \int_R^\infty \frac{GMm}{r^2} dr, \\ & = & \left[-\frac{GMm}{r}\right]_R^\infty, \\ & = & \frac{GMm}{R}. \end{eqnarray*}
(2) 重力エネルギーを運動エネルギーと等しいとおいて, \begin{eqnarray*} \frac{1}{2}mv^2 & = & \frac{GMm}{R}, \\ v & = & \sqrt{\frac{2GM}{R}}. \end{eqnarray*}
(3) \(M\),\(U\),\(v\) の計算結果は次の通りです. \begin{eqnarray*} M & = & 1.6755\times 10^{23}\ \mathrm{kg}, \\ U & = & 5.591\times 10^6\ \mathrm{J}, \\ v & = & 3.34\times 10^3\ \mathrm{m/s}. \end{eqnarray*}
(4) 温度の上昇 \(\Delta T\) は,求めたエネルギー \(U\) を物体の熱容量(質量\(\times\)比熱)で割って求めます. \[ \Delta T = 5590\ \mathrm{K}. \]
問題1-3-2 解答
(1) 地球については, \begin{eqnarray*} I_E & = & (2/5)\times 5.974\times10^{24}\times(6371\times 10^3)^2 = 9.699\times 10^{37}\ \mathrm{kg\,m^2},\\ \omega_E & = & 2\times 3.142/(0.9973\times 24\times 3600) = 7.293\times 10^{-5}\ \mathrm{s^{-1}},\\ L_E & = & 9.699\times 10^{37}\times 7.293\times 10^{-5} = 7.073\times 10^{33}\ \mathrm{kg\,m^2\,s^{-1}}. \end{eqnarray*} 金星については, \begin{eqnarray*} I_V & = & (2/5)\times 4.869\times10^{24}\times(6052\times 10^3)^2 = 7.133\times 10^{37}\ \mathrm{kg\,m^2},\\ \omega_V & = & 2\times 3.142/(243\times 24\times 3600) = 2.993\times 10^{-7}\ \mathrm{s^{-1}},\\ L_V & = & 7.133\times 10^{37}\times 2.993\times 10^{-7} = 2.135\times 10^{31}\ \mathrm{kg\,m^2\,s^{-1}}. \end{eqnarray*} よって, \[ L_V/L_E = 3.019\times 10^{-3} \approx 0.0030. \]
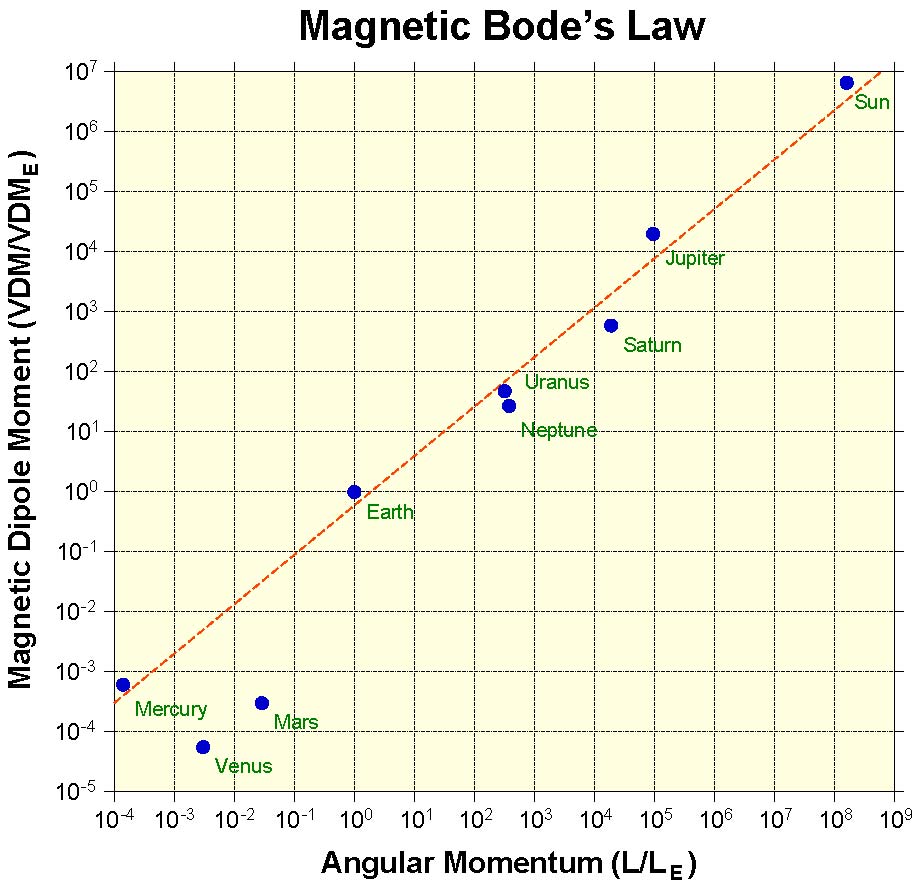
(2) 磁気的ボーデの法則は図のようになります.点線は金星と火星を除いて直線でフィットした結果です.火星はダイナモ作用が惑星形成後の比較的早い時期に停止したと考えられています.金星については,やはり遅い自転速度が原因のように思えますが,専門家の間では色々と議論になっています.水星も自転速度は遅く(自転周期は 59 日),角運動量も最小です.しかし,小さな惑星としては,惑星半径の 3/4 の大きい金属核があり,その流体部分でダイナモ作用が働いているようです.
問題1−3−3 解答
(1) ケプラーの第3法則 \(r^3\omega_L^2 = r'^3\omega_L'^2\) を, \[ \omega_L' = \left(\frac{r}{r'}\right)^{3\over2}\omega_L \] と表して,角運動量保存則, \[ I\omega + mr^2\omega_L = I\omega' + mr'^2\omega_L' \] に代入し \(\omega'\) を表わす式として変形すると問題の式が得られます.
(2) 定数などを代入して計算した結果は次の通りです. \begin{eqnarray*} \omega' & = & 3.03\times 10^{-4}\ \mathrm{s^{-1}} \quad (T \approx 5.8\ \mathrm{h}), \\ \omega_L' & = & 2.24\times 10^{-4}\ \mathrm{s^{-1}} \quad (T \approx 7.8\ \mathrm{h}). \end{eqnarray*}
(3) \(r'/r\) についての式を導きたいので,ケプラーの第3法則 \(r^3\omega_L^2 = r'^3\omega'^2\) を, \[ \omega' = \left(\frac{r'}{r}\right)^{-{3\over2}}\omega_L \] と表して,角運動量保存則, \[ I\omega + mr^2\omega_L = I\omega' + mr'^2\omega' \] に代入し,\((r'/r)^{1/2}\) を表わす式として変形します.
(4) 定数などを代入し有効数字5桁で表わすと,問い (3) の式は次のようになります. \[ \left(\frac{r'}{r}\right)^{1\over2} = 1.2450 - 8.9408\times 10^{-3}\left(\frac{r'}{r}\right)^{-{3\over2}}. \label{eq09} \] 逐次近似法による繰返し計算(iteration)の結果を3通りの初期値について表に示します.
| iteration | r'/r | ||
|---|---|---|---|
| initial | 1 | 0 | 2 |
| 1 | 1.5728 | 1.5500 | 1.5058 |
| 2 | 1.5397 | 1.5385 | 1.5380 |
| 3 | 1.5384 | 1.5384 | 1.5384 |
| 4 | 1.5384 | 1.5384 | 1.5384 |
よって,月公転軌道の半径は現在の約 1.5 倍となり,皆既日食は見られなくなります. \begin{eqnarray*} r' & = & 5.91\times 10^8\ \mathrm{m} \approx 59\ \mathrm{万km}, \\ \omega' & = & \omega_L' = = 1.394\times 10^{-6}\ \mathrm{s^{-1}} \quad (T \approx 52\ \mathrm{d}). \end{eqnarray*}