3-2 万有引力と重力
万有引力の法則とニュートンの運動方程式: 地球上で物体は重さに関係なく同時に落下することは,「1-2 運動方程式と万有引力」と重複しますが,万有引力の法則とニュートンの運動方程式を使用して,次のように導けます.
地球を半径 \(R\) の密度が一様な球と仮定し,質量を \(M\) とします.地球上の質量 \(m\) の物体は地球による引力 \(F\) を受けることで,ニュートンの運動方程式により加速度を得ますが,これを慣習上 \(g\) で表します.また,地球による引力は,地球中心に位置し地球と同じ質量 \(M\) の質点による万有引力と等しくなります.従って,万有引力定数を \(G\) として, \[ F = G\frac{Mm}{R^2} = mg, \] から重力加速度 \(g\) は, \[ g = \frac{GM}{R^2} \] となり,物体の質量 \(m\) には依存しないことが分かります.この式に \(G\) = 6.674\(\times\)10−11 m3 kg−1 s−2, \(M\) = 5.972\(\times\)1024 kg, \(R\) = 6.371\(\times\)106 m を代入すれば,重力加速度 \(g\) は約 9.8 m/s2 となります.
測地学では重力加速度を単に重力と呼びます.また,重力加速度の単位は CGS 単位系でガリレオ・ガリレイにちなんだガルを使い (Gal = cm/s2),「重力測定による重力は 980 Gal」などと表現します.しかしここでは,重力と重力加速度は区別して表現し,単位も SI 系の m/s2 を使うことにします.
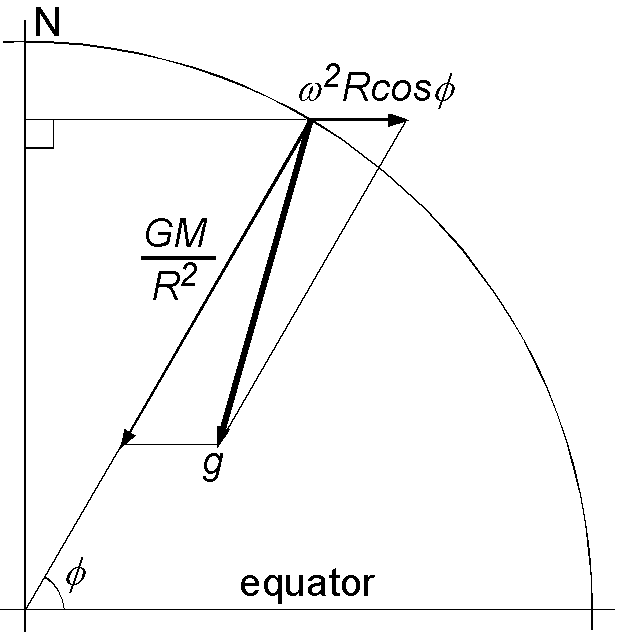
実際に地球上の物体が受ける重力は,地球自転で発生する遠心力がベクトルとして加わった力です.質量 \(m\) の質点が半径 \(r\) の円を描いて角速度 \(\omega\) で等速円運動を行なっている時に質点が受ける遠心力は, \[ mr\omega^2, \] です.よって,緯度 \(\phi\) における遠心力による加速度は自転軸と垂直で外向きに, \[ \omega^2R\cos\phi \] ですので,これを図のように引力による加速度とのベクトル和を取ると,実際の重力加速度となります.余弦定理を使用して, \[ g = \sqrt{\left(\frac{GM}{R^2}\right)^2 + (\omega^2R\cos\phi)^2 - \frac{2GM \omega^2\cos^2\phi}{R}} \] となります.特に,赤道と極での値 \(g_e\) と \(g_p\) はそれぞれ次のようになります. \[ g_e = \frac{GM}{R^2} - \omega^2R, \quad g_p = \frac{GM}{R^2}. \]
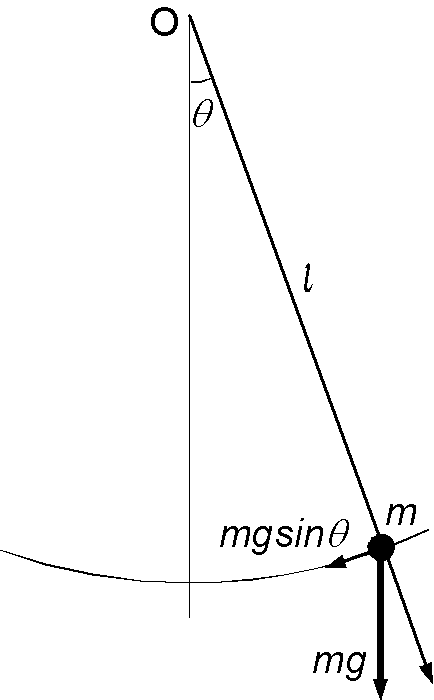
重力加速度の測定: 現代では重力加速度の測定は,真空中を落下する物体の落下距離と時間による絶対測定と,錘を吊るした石英のバネの伸びによる相対測定が主な方法です.しかし,歴史的には振り子の長さと周期による方法が広く行われ,重力加速度の緯度による違いなどが測定されました.現代でも学生実験で行われる,振り子による重力加速度の測定原理は以下の通りです.
質量 \(m\) の錘を長さ \(\ell\) の糸で吊した振子を考えます.振れの角度 \(\theta\) を反時計方向を正に取り,円弧に沿った加速度を \(a\) とすると,錘の運動方程式は, \[ F = ma = -mg\sin\theta, \] となります.円弧に沿った錘の速度 \(v\) はラジアン表示の \(\theta\) を使用して \(v = \ell (d\theta/dt)\) ですので,これを \(t\) で微分して, \[ a = \frac{dv}{dt} = \ell\frac{d^2\theta}{dt^2}, \] となり,また小さな \(\theta\) に対する \(\sin\theta\) の近似式, \[ \sin\theta \approx \theta, \] を使えば,運動方程式は次のようになります. \[ \frac{d^2\theta}{dt^2} = -\frac{g}{\ell}\theta. \] これは単振動の方程式で,解は \(A\) と \(\alpha\) を定数として, \[ \theta = A\cos(\sqrt{\frac{g}{\ell}}t - \alpha), \] となり,振動の周期 \(T\) は, \[ T = 2\pi\sqrt{\frac{\ell}{g}} \] となります.よって,振り子の長さ \(\ell\) と周期 \(T\) を測定すれば次式から重力加速度が求まります. \[ g = 4\pi^2\frac{\ell}{T^2}. \]
問題3-2-1
地球を半径 \(R\),質量 \(M\) の一様な球として,次の重力加速度と高さに関する問いに答えなさい.但し,自転による遠心力は考慮しないものとします.
- (1) 地表における重力加速度を \(g_0\) として,高さ \(h\) における重力加速度 \(g\) が次式で表されることを導きなさい. \[ g = g_0\left(1 + \frac{h}{R}\right)^{-2}. \]
- (2) 問い(1)で導いた式を,次の \(x\) が小さい場合に成り立つ近似式を用いて変形しなさい. \[ (1 + x)^{-2} \approx 1 - 2x \quad (|x| \ll 1). \]
- (3) 地表で測定した体重が 50 kg の人が高さ 320 m のビルで体重を測定すると何 g 減少した表示となるか,地球半径を 6400 km として計算しなさい.但し,体重計は天秤ではないとし,またビルの質量による引力は無視します.
問題3-2-2
地球を球として,万有引力と自転による遠心力についての次の問いに答えなさい.
- (1) 引力による加速度 \(GM/R^2\) と 赤道上での遠心力による加速度 \(\omega^2 R\) を計算しなさい.但し,次の定数を使用し,単位は m/s2 で小数点以下3桁まで求めるものとします. \begin{eqnarray*} G & = & 6.674\times 10^{−11}\ \mathrm{m^3\,kg^{−1}\,s^{−2}},\\ M & = & 5.972\times 10^{24}\ \mathrm{kg},\\ R & = & 6.371\times 10^6\ \mathrm{m},\\ \omega & = & 2\pi\div(0.9973\times 24\times 3600) = 7.292\times 10^{-5}\ \mathrm{s^{-1}}. \end{eqnarray*}
- (2) 北極で測定した体重が 50 kg の人が,同じ体重計を使用して赤道で体重を測定すると何 g 小さい値を示すか? 但し,体重計は天秤ではないとします.
- (3) 地球表面で物体が東に向かって運動すると,地球の自転による円運動の速度に物体の速度が加わり,物体に働く遠心力が増加します.その結果,物体に働く重力加速度は減少します.物体が西向きに運動する場合はこの逆となります.これをエトベス効果といいます.では,赤道上で東向きに速度 \(v\) で運動する物体に働く遠心力による加速度は, \[ \frac{(\omega R + v)^2}{R} \approx \omega^2 R + 2v\omega, \] となり,静止状態に比べて \(2v\omega\) 増えることを示しなさい.但し, \(v\) は地球表面の自転速度 \(\omega R\) に比べて小さく(\(v \ll \omega R\)),次の近似式を使用します. \[ (1+x)^2 \approx 1 + 2x \quad (|x| \ll 1). \]
- (4) 北極で測定した体重が 50 kg の人が赤道上を東に 1 m/s の速度で運動するとき,エトベス効果による体重のみかけの減少は何 g か?
補足: エトベス効果は → 3-4 自転とコリオリ力や → 問題3-4-1で学ぶコリオリ力の鉛直成分です.
問題3-2-3
天体の自転速度が何らかの理由で増大し,赤道での遠心力が天体自身の万有引力(自己重力)と等しくなると天体は破壊されます.
- (1) 密度 \(\rho\) の天体について,この限界の自転の角速度 \(\omega\) は万有引力定数 \(G\) を用いて次式となることを導きなさい. \[ \omega = \sqrt{\frac{4\pi}{3}G\rho}. \]
- (2) 地球の密度を5500 kg/m \(^3\) として,破壊の限界の自転周期を求めなさい.