問題1-3-3 解説
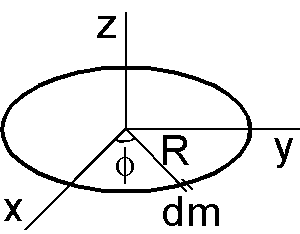
(a) z 軸の回りの慣性モーメント \(I_z\) は,図の微小質量 \(dm\) の慣性モーメント \(dm\times R^2\) を円環に沿って積分します.微小質量は \(dm=\tau\times Rd\phi\) ですので, \begin{eqnarray*} I_z & = & \int R^2 dm = \int_0^{2\pi}R^2\tau R d\phi = \tau R^3\int_0^{2\pi}d\phi, \\ & = & (2\pi R\tau)R^2 = MR^2. \end{eqnarray*} x 軸の回りの慣性モーメント \(I_x\) は, \(dm\) の座標を \((x,y)\) として \(dm\times y^2\) を円環に沿って積分します. \begin{eqnarray*} I_x & = & \int y^2 dm = \int_0^{2\pi}(R\sin\phi)^2\tau R d\phi = \tau R^3\int_0^{2\pi}\sin^2\phi d\phi, \\ & = & \tau R^3\int_0^{2\pi}\frac{1-\cos 2\phi}{2}d\phi = \tau R^3\left[\frac{\phi}{2}-\frac{\sin 2\phi}{4}\right]_0^{2\pi} = \pi\tau R^3,\\ & = & \frac{1}{2}(2\pi R\tau)R^2 = \frac{1}{2}MR^2. \end{eqnarray*} \(I_y\) についても \(\int x^2 dm\) を同様に積分して, \[ I_y = \frac{1}{2}MR^2. \]
(a)の別解: 円環に沿った \(dm\) の積分は \(M\) ですので \(I_z\) は, \[ I_z = \int R^2 dm = R^2\int dm = MR^2 \] \(I_x\) と \(I_y\) については,両者の和を取り,対称性から \(I_x=I_y\) ですので, \begin{eqnarray*} I_x + I_y & = & \int y^2 dm + \int x^2 dm, \\ 2I_x = 2I_y & = & \int(x^2+y^2)dm = \int R^2 dm = MR^2, \\ I_x = I_y & = & \frac{1}{2}MR^2. \end{eqnarray*}
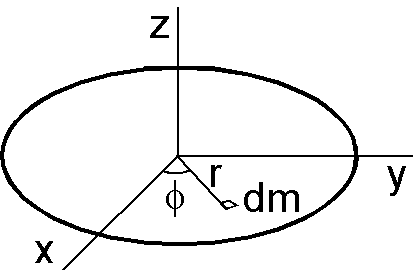
(b) \(I_z\) は微小質量 \(dm\) の慣性モーメント \(dm\times r^2\) を円盤全面で積分します.微小質量は \(dm=\sigma\times dr\times rd\phi\) ですので, \begin{eqnarray*} I_z & = & \int r^2 dm = \sigma\int_0^R\int_0^{2\pi}r^3 dr d\phi = 2\pi\sigma\int_0^R r^3 dr, \\ & = & 2\pi\sigma\frac{R^4}{4} = \frac{1}{2}(\pi R^2\sigma)R^2 = \frac{1}{2}MR^2. \end{eqnarray*} \(I_x\) は \(dm\times y^2\) を積分します. \begin{eqnarray*} I_x & = & \int y^2 dm = \sigma\int_0^R\int_0^{2\pi}r^3\sin^2\phi dr d\phi = \sigma\int_0^R r^3 dr\int_0^{2\pi}\frac{1-\cos 2\phi}{2}d\phi, \\ & = & \sigma\frac{R^4}{4}\left[\frac{\phi}{2}-\frac{\sin 2\phi}{4}\right]_0^{2\pi} = \frac{1}{4}\pi\sigma R^4 = \frac{1}{4}(\pi R^2\sigma)R^2 = \frac{1}{4}MR^2. \end{eqnarray*} \(I_y\) も \(dm\times x^2\) を同様に積分して, \[ I_y = \frac{1}{4}MR^2. \]
(b)の別解: (a) で導いた円環の慣性モーメントの式を利用します.半径 \(r\) で 幅 \(dr\) の円環の質量は \(\sigma\times 2\pi r\times dr\) ですので,この円環の z 軸の回りの慣性モーメントを \(dI_z\) で表わせば, \[ dI_z = (2\pi\sigma r dr)r^2 = 2\pi\sigma r^3 dr. \] これを積分して, \[ I_z = 2\pi\sigma\int_0^R r^3 dr = \frac{1}{2}\pi\sigma R^4 = \frac{1}{2}MR^2. \] 同様にして, \[ dI_x = dI_y = \frac{1}{2}(2\pi\sigma r dr)r^2 = \pi\sigma r^3 dr. \] 積分して, \[ I_x = I_y = \pi\sigma\int_0^R r^3 dr = \frac{1}{4}\pi\sigma R^4 = \frac{1}{4}\left(\pi R^2\sigma\right)R^2 = \frac{1}{4}MR^2. \]
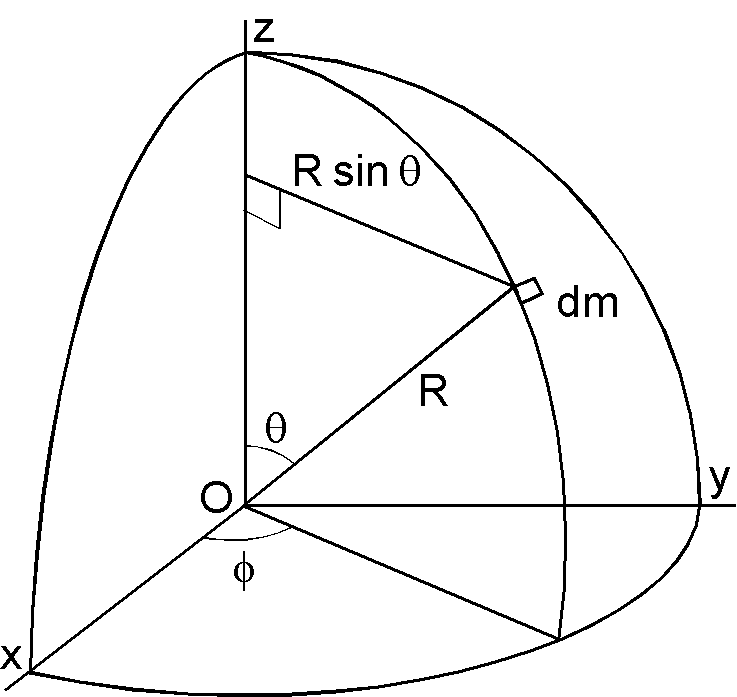
(c) 球殻の慣性モーメントは対称性から軸の向きは任意ですが,ここでは図のように座標軸を取ります(簡略化した図は全体の8分の1です).微小質量 \(dm\) の z 軸の回りの慣性モーメント \(dm\times(R\sin\theta)^2\) を球殻全面で積分します.微小質量は \(dm=\sigma\times Rd\theta\times R\sin\theta d\phi\) ですので, \begin{eqnarray*} I & = & \int (R\sin\theta)^2 dm = \sigma R^4\int_0^\pi\int_0^{2\pi}\sin^2\theta\sin\theta d\theta d\phi, \\ & = & 2\pi\sigma R^4\int_0^\pi(1-\cos^2\theta)\sin\theta d\theta, \\ & = & 2\pi\sigma R^4\int_{-1}^1(1-t^2)dt = 2\pi\sigma R^4\left[t-\frac{t^3}{3}\right]_{-1}^1, \\ & = & \frac{8}{3}\pi\sigma R^4 = \frac{2}{3}(4\pi R^2\sigma)R^2 = \frac{2}{3}MR^2. \end{eqnarray*} 上の積分では, \(t=\cos\theta\) (\(dt=-\sin\theta d\theta\)) の変数変換を利用しました.
(c)の別解: 微小質量 \(dm\) の座標を \((x,y,z)\) とすると, \[ I_x = \int(y^2+z^2)dm, \quad I_y = \int(z^2+x^2)dm, \quad I_z = \int(x^2+y^2)dm. \] これらを辺々加えると, \[ I_x + I_y + I_z = 2\int(x^2+y^2+z^2)dm. \] \(I_x=I_y=I_z=I\) と置き, \(x^2+y^2+z^2=R^2\) ですので, \begin{eqnarray*} 3I & = & 2R^2\int dm = 2R^2M, \\ I & = & \frac{2}{3}MR^2. \end{eqnarray*}
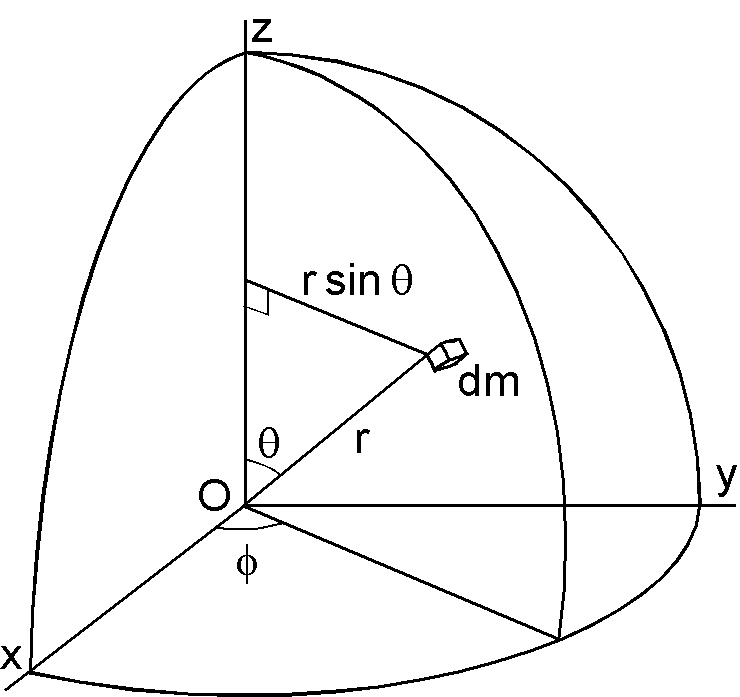
(d) 球では微小質量 \(dm\) の z 軸の回りの慣性モーメント \(dm\times(r\sin\theta)^2\) を球全体で積分します.微小質量は \(dm=\rho\times dr\times rd\theta\times r\sin\theta d\phi\) ですので, \begin{eqnarray*} I & = & \int (r\sin\theta)^2 dm, \\ & = & \rho\int_0^R\int_0^\pi\int_0^{2\pi}r^4\sin^2\theta\sin\theta dr d\theta d\phi, \\ & = & 2\pi\rho\frac{R^5}{5}\int_0^\pi(1-\cos^2\theta)\sin\theta d\theta, \\ & = & 2\pi\rho\frac{R^5}{5}\int_{-1}^1(1-t^2)dt = 2\pi\rho\frac{R^5}{5}\left[t-\frac{t^3}{3}\right]_{-1}^1, \\ & = & 2\pi\rho\frac{R^5}{5}\frac{4}{3} = \frac{2}{5}\left(\frac{4}{3}\pi R^3\rho\right)R^2 = \frac{2}{5}MR^2. \end{eqnarray*}
(d)の別解: (c) の別解と同様に \(I_x+I_y+I_z=3I\) として \(r^2dm\) を積分します. \begin{eqnarray*} I_x + I_y + I_z & = & 2\int(x^2+y^2+z^2)dm, \\ 3I & = & 2\int r^2 dm, \\ I & = & \frac{2}{3}\int_0^R\int_0^\pi\int_0^{2\pi}r^2\ \rho r^2\sin\theta dr d\theta d\phi, \\ & = & \frac{4}{3}\pi\rho\int_0^R r^4 dr\int_0^\pi\sin\theta d\theta, \\ & = & \frac{4}{3}\pi\rho\frac{R^5}{5}\left[-\cos\theta\right]_0^\pi, \\ & = & \frac{4}{3}\pi\rho\frac{R^5}{5}2 = \frac{2}{5}\left(\frac{4}{3}\pi R^3\rho\right)R^2 = \frac{2}{5}MR^2. \end{eqnarray*}
(d)の別解2: (c) で導いた球殻の慣性モーメントの式を利用します.半径 \(r\) で 厚さ \(dr\) の球殻の質量は \(\rho\times 4\pi r^2\times dr\) ですので,この球殻の慣性モーメントを \(dI\) で表わせば, \[ dI = \frac{2}{3}(4\pi\rho r^2 dr)r^2 = \frac{8}{3}\pi\rho r^4 dr. \] これを積分して, \[ I = \frac{8}{3}\pi\rho\int_0^R r^4 dr = \frac{8}{3}\pi\rho\frac{R^5}{5} = \frac{2}{5}\left(\frac{4}{3}\pi R^3\rho\right)R^2 = \frac{2}{5}MR^2. \]