単磁区粒子の非履歴性残留磁化:熱活性化理論モデル
プライザッハ・ダイアグラムを用いた ARM モデルは,磁気的相互作用の働いている単磁区粒子のみに適用されます.磁気的相互作用のない単磁区粒子では, ARM 強度は極めて小さな直流磁場 \(H_D\) の基でも飽和してしまいます.無限大の ARM 帯磁率,即ち \(\partial ARM/\partial H_D = \infty\),の問題は,ネールの熱活性化理論を用いた Jaep (1969) のモデルにより解決されました.
熱活性化を考慮した ARM 獲得の理論
容易軸が一方向に揃った \(N\) 個のマグネタイトの単磁区粒子の集団を考えます.いま,方形波の交流磁場を容易軸方向に掛け,小さな直流磁場 \(H_D\) を重ねて掛けます.
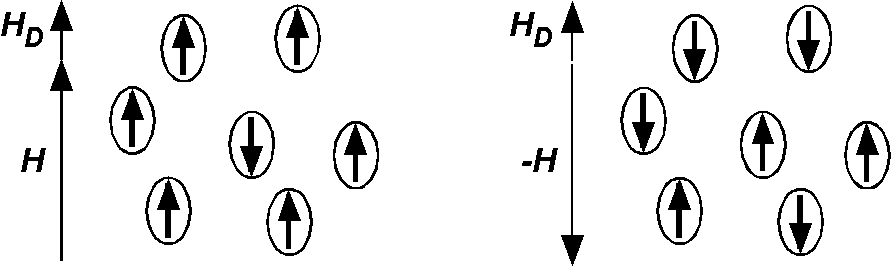
\(H_D\) 方向を正とし,正と負の磁化の数をそれぞれ \(N_1\) と \(N_2\) とします(\(N = N_1 + N_2\)).正の磁場 \(H\) が掛かる半周期では(左図),磁化の \(-H\) 方向への回転はめったに発生しないと考えられます.よって, \begin{equation} \frac{dN_1}{dt} = \frac{1}{\tau_+}N_2, \label{eq01} \end{equation} ここに, \(\tau_+\) は \(-H\) から \(H\) 方向への回転の緩和時間です.ここで,規格化された磁化 \(p\) を導入します. \begin{equation} p = \frac{N_1 - N_2}{N}. \label{eq02} \end{equation} 式 (1) を用い, \(dN_1/dt = -dN_2/dt\) と \(p = 1 - 2N_2/N\) に注意して, \[ \frac{dp}{dt} = \frac{1}{N}\left(\frac{dN_1}{dt} - \frac{dN_2}{dt}\right) = \frac{2}{N}\frac{dN_1}{dt} = \frac{1}{\tau_+}\frac{2}{N}N_2 = \frac{1-p}{\tau_+}. \] この式を積分すると, \begin{align*} -\frac{dp}{1-p} & = -\frac{dt}{\tau_+}, \\ \log(1-p) & = -t/\tau_+ + C, \\ p & = 1 - Ke^{-t/\tau_+}, \end{align*} ここに, \(C\) と \(K\) は積分定数です. \(t = 0\) で \(p = p_0\) として,次式を得ます. \begin{equation} p = 1 - (1 - p_0)e^{-t/\tau_+}. \label{eq03} \end{equation} 負の磁場 \(-H\) の半周期では(右図), \begin{equation} \frac{dN_2}{dt} = \frac{1}{\tau_-}N_1. \label{eq04} \end{equation} ここに, \(\tau_-\) は \(H\) から \(-H\) 方向への回転の緩和時間です.同様にして, \begin{align*} \frac{dp}{dt} & = \frac{1}{N}\left(\frac{dN_1}{dt} - \frac{dN_2}{dt}\right) = -\frac{2}{N}\frac{dN_2}{dt} = -\frac{1}{\tau_-}\frac{2}{N}N_1 = -\frac{1+p}{\tau_-}, \\ \frac{dp}{1+p} & = -\frac{dt}{\tau_-}. \end{align*} この式を \(t=0\) で \(p=p_0\) として積分して次式を得ます. \begin{equation} p = -1 + (1 + p_0)e^{-t/\tau_-}. \label{eq05} \end{equation}
いま, \(H_D\) を掛けたまま交流磁場の振幅を次第にゼロまで減少させます(下図).
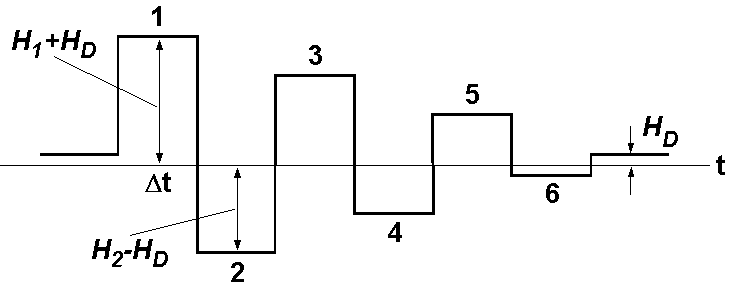
\(n\) を奇数とし, \(n\) 番目と \(n\)+1 番目の交流磁場の振幅をそれぞれ \(H_n\) と \(-H_{n+1}\) とします.それぞれの半周期における \(p_n\) と \(p_{n+1}\) の方程式は (3) と (5) となります.緩和時間 \(\tau_+\) と \(\tau_-\) は前のページで示した「\(\tau_{21}\)」ですが,それぞれ \(H\) を \(H_n+H_D\) と \(H_{n+1}-H_D\) で置き換えます.よって, ARM 獲得モデルを支配する方程式は次のようになります.但し, \(A\) = 109 s-1 です. \begin{eqnarray} p_n & = & 1 - (1 - p_{n-1})e^{-\Delta t/\tau_n}, \label{eq06} \\ \tau_n & = & \frac{1}{A}\exp\left[\frac{\mu_0 VM_s H_K}{2kT}\left(1-\frac{H_n+H_D}{H_K}\right)^2\right], \label{eq07} \\ p_{n+1} & = & -1 + (1 + p_n)e^{-\Delta t/\tau_{n+1}}, \label{eq08} \\ \tau_{n+1} & = & \frac{1}{A}\exp\left[\frac{\mu_0 VM_s H_K}{2kT}\left(1-\frac{H_{n+1}-H_D}{H_K}\right)^2\right]. \label{eq09} \end{eqnarray}
シミュレーションの例
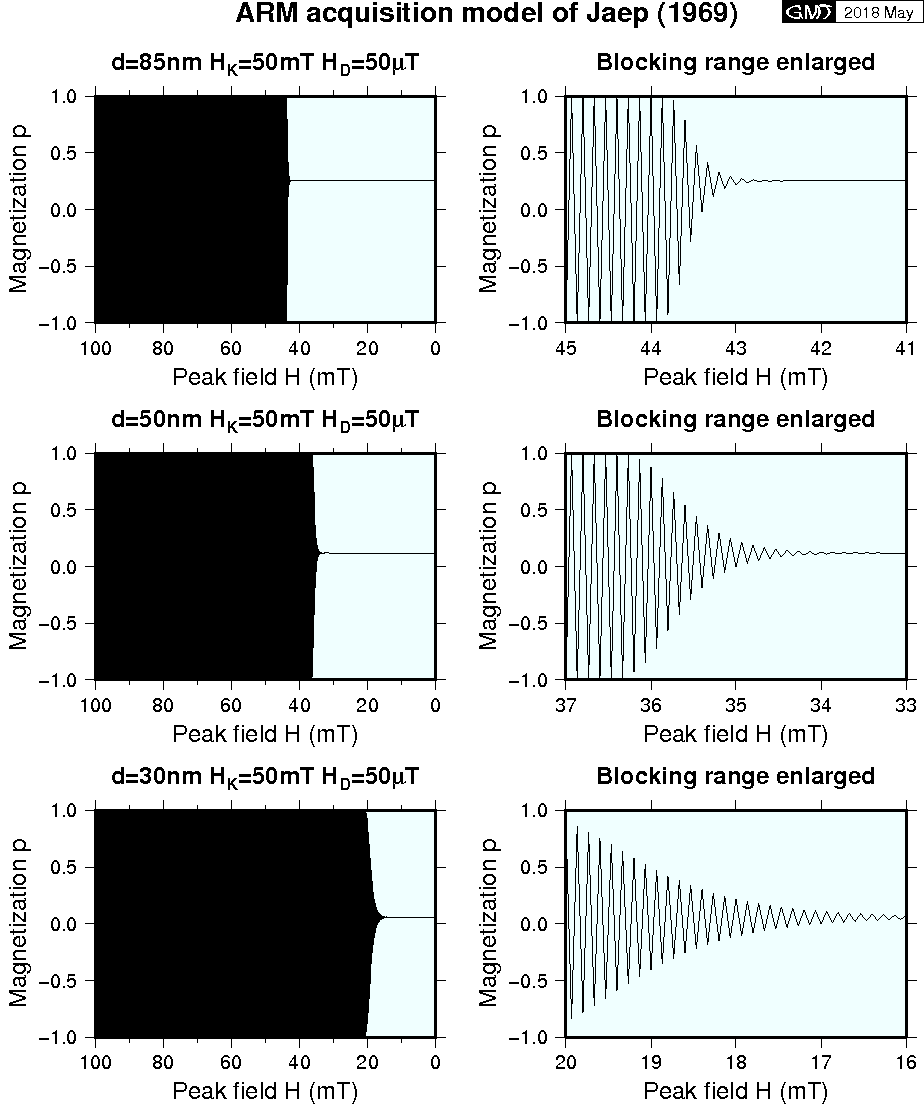
式 (6) ~ (9) を用い,振幅 100 mT で 50 Hz の交流磁場を 30 s で減少させてシミュレーションを行いました.下図に,微視的保磁力 \(H_K\) = 50 mT,直流磁場 \(H_D\) = 0.05 mT (50 μT) として, ARM ブロッキングの様子を粒子の直径 \(d\) = 85 nm (上), 50 nm (中), 30 nm (下)の代表的な3例について示します.図から,ブロッキング磁場 \(H_B\) は常に \(H_K\) よりも小さいことが分かりますが,これは室温でさえ熱エネルギーの入力があるためです.同じ理由で,粒径が小さいほど \(H_B\) は小さく, \(H_B\) の範囲が広くなります.ブロックされた磁化 \(p\) も小さい粒径ほど小さくなります.
ブロックされた \(p\) の理論式
Jaep (1969) はまた, ARM 強度の理論的表現が \(p_{n-1} = p_{n+1}\) として得られることを示しましたが,これを以下に解説します.式 (6) を書き直して, \[ 1 - p_n = (1 - p_{n-1})e^{-\Delta t/\tau_n}, \] そして, (8) の両辺に \(e^{\Delta t/\tau_{n+1}}\) を掛けて, \[ 1 + p_n = (1 + p_{n+1})e^{\Delta t/\tau_{n+1}}. \] この2式を足して, \(p=p_{n-1}=p_{n+1}\) と記すと, \[ 2 = (1 - p)e^{-\Delta t/\tau_n} + (1 + p)e^{\Delta t/\tau_{n+1}}. \] ブロッキングにおいては, \(\Delta t/\tau_n, \Delta t/\tau_{n+1} \ll 1\) となるので,近似式 \(e^x \approx 1+x\) (\(|x| \ll 1\)) を用いて, \[ 2 = (1 - p)(1 - \Delta t/\tau_n) + (1 + p)(1 + \Delta t/\tau_{n+1}), \] これより次式を得ます. \[ p = \frac{\Delta t/\tau_n - \Delta t/\tau_{n+1}}{\Delta t/\tau_n + \Delta t/\tau_{n+1}} = \frac{\tau_{n+1} - \tau_n}{\tau_{n+1} + \tau_n}. \] この式に (7) と (9) を代入して, \[ p = \frac{\exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1+\frac{H_D}{H_K}-\frac{H_{n+1}}{H_K}\right)^2\right] - \exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1-\frac{H_D}{H_K}-\frac{H_n}{H_K}\right)^2\right]} {\exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1+\frac{H_D}{H_K}-\frac{H_{n+1}}{H_K}\right)^2\right] + \exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1-\frac{H_D}{H_K}-\frac{H_n}{H_K}\right)^2\right]}. \] 交流磁場の振幅を \(H_{n+1} \approx H_n = H_B\) と近似し, \(p\) は次のように変形されます. \begin{eqnarray} p &=& \frac{\exp\left[\frac{\mu_0VM_sH_D}{kT}\left(1-\frac{H_B}{H_K}\right)\right] - \exp\left[-\frac{\mu_0VM_sH_D}{kT}\left(1-\frac{H_B}{H_K}\right)\right]} {\exp\left[\frac{\mu_0VM_sH_D}{kT}\left(1-\frac{H_B}{H_K}\right)\right] + \exp\left[-\frac{\mu_0VM_sH_D}{kT}\left(1-\frac{H_B}{H_K}\right)\right]}, \nonumber \\ &=& \tanh\left[\frac{\mu_0VM_sH_D}{kT}\left(1-\frac{H_B}{H_K}\right)\right]. \label{eq10} \end{eqnarray} ブロッキング磁場 \(H_B\) は次の緩和時間 \(\tau_B\) を 1 s と置くことで決定されます. \begin{equation} \tau_{n+1} \approx \tau_n = \tau_B= \frac{1}{A}\exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1-\frac{H_B}{H_K}\right)^2\right] = 1. \label{eq11} \end{equation}
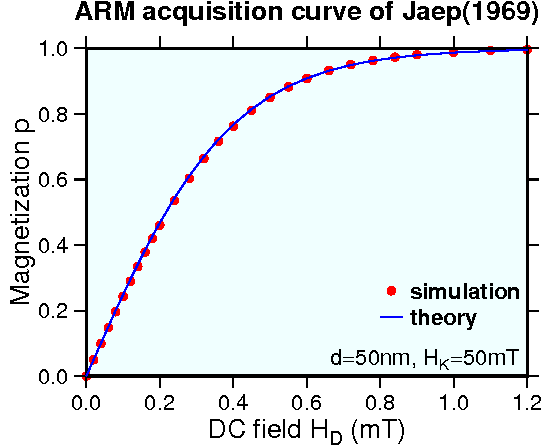
右図は \(d\) = 50 nm, \(H_K\) = 50 mT についての ARM 獲得曲線がシミュレーション(赤丸)と理論(青線)で大変よく一致していることを示します.しかし,モデルの ARM 帯磁率 \(\partial p/\partial H_D\) は実験的観測結果よりもずっと大きく,モデルが一方向に揃った単磁区粒子についてで,ランダムな分布の粒子ではないことを考慮しても大きすぎます.モデルと観測の違いは, ARM では磁気的相互作用が強いことが原因です.磁気的相互作用の影響は TRM よりも ARM で大きいです.この理由は, ARM は自発磁化 \(M_s\) が大きく相互作用磁場が強い室温でブロックされるのに対して, TRM は \(M_s\) が小さい高温でブロックされるからです.それでも, Jaep の ARM モデルは磁気的相互作用の無い単磁区粒子に対しても有限の ARM 帯磁率を与える点で,プライザッハ・モデルよりも優れていると言えます.
Jaep (1971) は磁気的相互作用のある単磁区粒子に対する,ネールの熱活性化理論を用いたモデルを追加しました.この ARM モデルに基づいて, Tanaka (1999) はショー(Shaw)法による古地磁気強度測定における ARM 補正に関して, ARM と TRM の類似性について議論しています.
参考文献:
- Jaep, W. F., Anhysteretic magnetization of an assembly of single-domain particles, J. Appl. Phys., 40, 1297-1298, 1969.
- Jaep, W. F., Role of interactions in magnetic tapes, J. Appl. Phys., 42, 2790-2794, 1971.
- Tanaka, H., Theoretical background of ARM correction in the Shaw palaeointensity method, Geophys. J. Int., 137, 261-265, 1999. (→ doi:10.1046/j.1365-246X.1999.00783.x)