5-4 海洋リソスフェアの半無限体冷却モデル
海洋リソスフェアの熱流量: 海洋地域で観測される地殻熱流量は,「5-1 地温勾配と地殻熱流量」でも言及しましたが,発熱源の放射性元素含有量が小さいにもかかわらず大陸地域よりも大きいです.海洋底で観測される熱流量は,海嶺付近では 200~250 mW/m2 以上にもなり,海嶺から離れるに従い減少します.また,海洋リソスフェアの厚さは海嶺から離れるに従い厚くなり,海洋底も深くなります.これらの観測結果はプレートテクトニクスの海洋底拡大に伴うリソスフェアの冷却過程で説明されます.
海嶺ではアセノスフェアとよばれる高温のマントル物質が上昇してきます.アセノスフェアは固体ですが,地質学的時間スケールではマントル対流に従って流動すると考えられています.上昇してきたアセノスフェアは海底で冷却されて上部から段々と固くなりますが,その領域をリソスフェアとよびます(なお,プレートも同じ領域を指す用語ですが,太平洋プレートなど,リソスフェアの個々のブロックに使用することが多いようです).リソスフェアは時間とともに冷却が進み厚さが増加し,海洋底拡大に伴い海嶺から離れていきます.リソスフェアの密度は冷却とともに増加し,アイソスタシーにより時間とともに沈降が進み,海嶺から離れるほど海洋底は深くなります.このような海洋リソスフェアの冷却モデルによる地殻熱流量の理論値は種々の年代の海底で測定値とよく一致します.
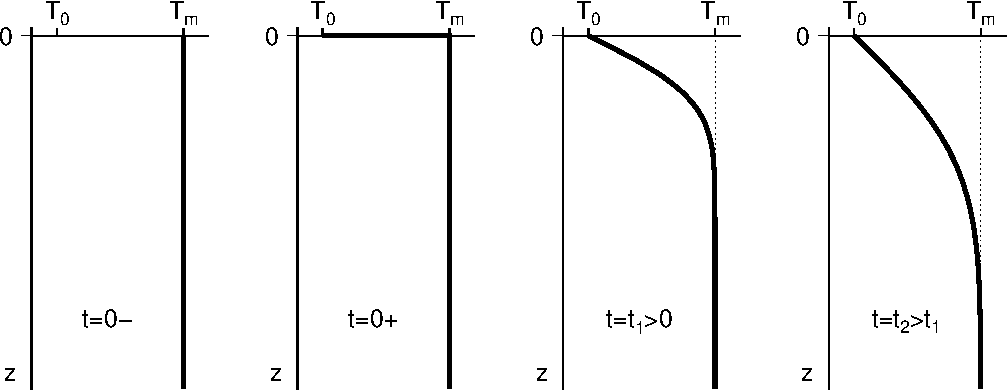
海洋リソスフェアの半無限体冷却モデルによる地下温度分布を時間を追って下図に示します.このモデルでは,アセノスフェアを柱状の半無限体とし,表面の海底を原点として深さ方向に \(z\) 軸を取ります.アセノスフェアは海洋底拡大に伴い水平方向に移動しますが,座標軸は移動するアセノスフェアに固定されているとします.また,水平方向の熱伝導はないものとします.時間の原点 \(t\) = 0 で温度 \(T_m\) のアセノスフェアの上面が突然に海底の温度 \(T_0\) に冷却されるとして,1次元非定常熱伝導方程式を解きます. \(t\) = 0- と \(t\) = 0+ はそれぞれ \(z\) = 0 が \(T_0\) に冷却される直前と直後の地下温度分布です.その後の \(t\) = \(t_1\) で冷却が深部に浸透し,更に時間の経過した \(t\) = \(t_2\) でより深い部分まで冷却が進行している様子が示されています.このモデルによる非定常熱伝導方程式の解法を Turcotte & Schubert (2002) に従って以下に説明します.解析は少し長くなりますが,基礎レベルの数学でも十分理解できる内容です.
半無限体冷却モデル: 深さと時間の関数である温度 \(T(z,t)\) に対する1次元非定常熱伝導方程式, \begin{equation} \frac{\partial T}{\partial t} = \kappa \frac{\partial^2 T}{\partial z^2}, \label{eq01} \end{equation} を境界条件, \begin{equation} T(z,0)=T_m, \quad T(0,t)=T_0, \quad T(\infty,t)=T_m, \label{eq02} \end{equation} のもとに解きます.まず,次の無次元温度 \(\theta(z,t)\) を導入します. \begin{equation} \theta=\frac{T-T_0}{T_m-T_0}. \label{eq03} \end{equation} 簡単に分かるように, \(\theta\) に関する熱伝導方程式の形は (1) と同じで, \begin{equation} \frac{\partial \theta}{\partial t} = \kappa \frac{\partial^2 \theta}{\partial z^2}. \label{eq04} \end{equation} 境界条件は次のようになります. \begin{equation} \theta(z,0)=1, \quad \theta(0,t)=0, \quad \theta(\infty,t)=1, \label{eq05} \end{equation} さらに,変数 \(z\) を \(2\sqrt{\kappa t}\) で規格化し,無次元とした新しい変数 \(\eta\) を導入します. \begin{equation} \eta = \frac{z}{2\sqrt{\kappa t}}. \label{eq06} \end{equation} ここに, \(\sqrt{\kappa t}\) は時間 \(t\) に対する熱拡散の特徴的距離で,分母の \(2\) は後の式変形を容易にするためです.2つの変数 \(z\) と \(t\) から1つの無次元変数となった \(\eta\) は相似変数とよばれます.その由来は, \(T\) を \(z\) に対してプロットした曲線は \(t\) が異なれば違う形ですが, \(z\) を \(2\sqrt{\kappa t}\) で規格化してプロットすれば同じ形になるからです.
式 (4) を \(\eta\) で表わすために,次のように偏微分の変換を実行します. \begin{eqnarray*} \frac{\partial\theta}{\partial t} & = & \frac{d\theta}{d\eta}\frac{\partial\eta}{\partial t} = \frac{d\theta}{d\eta}\left(-\frac{1}{4}\frac{z}{\sqrt{\kappa t}}\frac{1}{t}\right) = -\frac{\eta}{2t}\frac{d\theta}{d\eta}, \\ \frac{\partial\theta}{\partial z} & = & \frac{d\theta}{d\eta}\frac{\partial\eta}{\partial z} = \frac{1}{2\sqrt{\kappa t}}\frac{d\theta}{d\eta}, \\ \frac{\partial^2\theta}{\partial z^2} & = & \frac{1}{2\sqrt{\kappa t}}\frac{d}{d\eta}\left(\frac{d\theta}{d\eta}\right)\frac{d\eta}{dz} = \frac{1}{4\kappa t}\frac{d^2\theta}{d\eta^2}. \end{eqnarray*} これらを用いると式 (4) は, \[ -\frac{\eta}{2t}\frac{d\theta}{d\eta} = \frac{\kappa}{4\kappa t}\frac{d^2\theta}{d\eta^2}, \] となり,熱伝導方程式 (4) と境界条件 (5) は次のようになります. \begin{equation} -\eta\frac{d\theta}{d\eta} = \frac{1}{2}\frac{d^2\theta}{d\eta^2}, \label{eq07} \end{equation} \begin{equation} \theta(0) = 0, \quad \theta(\infty) = 1. \label{eq08} \end{equation}
ここで, \(\phi=\frac{d\theta}{d\eta}\) とおくと式 (7) は, \begin{eqnarray*} -\eta\phi & = & \frac{1}{2}\frac{d\phi}{d\eta}, \\ -2\eta d\eta & = & \frac{d\phi}{\phi}, \end{eqnarray*} となり,これを両辺積分します.簡単のために,積分定数を \(-\log C_1\) とおくと, \begin{eqnarray*} & & -\eta^2 = \log\phi - \log C_1 = \log\frac{\phi}{C_1}, \\ & & \qquad \phi = \frac{d\theta}{d\eta} = C_1 e^{-\eta^2}. \end{eqnarray*} これを更に積分しますが, \(e^{-\eta^2}\) の不定積分は初等関数では表わせないので,任意の変数 \(t\) を用いて次の表現とします. \[ \theta(\eta) = C_1\int_0^\eta e^{-t^2}dt + C_2. \] ここで境界条件 (8) を適用すると, \(\theta(0)\) = 0 より \(C_2\) = 0 で, \(\theta(\infty)\) = 1 より, \[ 1 = C_1\int_0^\infty e^{-t^2}dt. \] 右辺の定積分は \(\frac{\sqrt{\pi}}{2}\) ですので(→ 導き方), \(C_1\) = \(\frac{2}{\sqrt{\pi}}\) となり \(\theta\) は次式となります. \begin{equation} \theta(\eta) = \frac{2}{\sqrt{\pi}}\int_0^\eta e^{-t^2}dt. \label{9} \end{equation} この式の右辺は誤差関数とよばれ,正規分布の累積分布関数を与えるなど,科学技術の広い分野で使用され,記号 \({\rm erf}()\) で表わされます(誤差関数 \({\rm erf}(x)\) と相補誤差関数 \({\rm erfc}(x)\) = 1 - \({\rm erf}(x)\) のグラフと数値表は → このページにあります).結局,海洋リソスフェアの冷却モデルは次式で与えられます. \begin{equation} \frac{T(z,t)-T_0}{T_m-T_0} = {\rm erf}\left(\frac{z}{2\sqrt{\kappa t}}\right). \label{10} \end{equation}
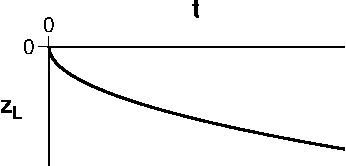
海洋リソスフェアの厚さの時間変化: この半無限体冷却モデルで表面付近の急な温度変化の領域を熱境界層とよびます.ここでは,熱境界層の厚さを \(T-T_0\) が \(T_m-T_0\) の 0.9 になるまでとして,その領域をリソスフェアとします.すると, \({\rm erf}(\eta)\) = 0.9 となる \(\eta\) はおよそ 1.16 ですので,リソスフェアの底の深さ,即ちリソスフェアの厚さ \(z_L\) は, \begin{equation} z_L = 2.32\sqrt{\kappa t}, \label{11} \end{equation} で与えられ,図のように時間 \(t\) の経過とともに厚くなります.さらに,温度の低いリソスフェアはアセノスフェアよりも密度が大きいため,厚さの増大につれてアイソスタシーにより次第に沈降します.そのため図にはありませんが,海洋底は時間とともに深くなります.実際の海洋底の深さやリソスフェアの厚さは,若い年代ではこのモデルでよく説明できます.しかし,およそ8千万年前より古くなると,例えば海洋底の深さやリソスフェアの厚さが一定値に近づくなど,このモデルでは十分には説明できなくなります.専門レベルになりますが,古い時代のデータも含めて説明可能なモデルが提唱されています.
海洋リソスフェアの熱流量の時間変化: 半無限体冷却モデルによる地殻熱流量は式 (10) を \(z\) で微分して熱伝導度 \(k\) を掛けることで得られます.誤差関数の微分は一般に, \[ \frac{d}{dx}{\rm erf}(x) = \frac{d}{dx}\left(\frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}dt\right) = \frac{2}{\sqrt{\pi}}e^{-x^2}, \] ですので,式 (10) より熱流量 \(q\) は, \[ q = -k\frac{\partial T}{\partial z} = -\frac{k(T_m-T_0)}{\sqrt{\pi\kappa t}}e^{-z^2/4\kappa t}, \] となります.リソスフェア表面,即ち海洋底での地殻熱流量 \(q_0\) は \(z\) = 0 とおいて, \begin{equation} q_0 = -\frac{k(T_m-T_0)}{\sqrt{\pi\kappa t}}, \label{eq12} \end{equation} となります.この式では \(t\) = 0 で \(q_0\) が無限大になりますが,その点を除いて式 (12) は観測値とよく合います.しかし,前述のリソスフェアの厚さと同様,約8千万年前より古い海底では観測値が一定になるなど,モデルとの差が現れます.これについてはより詳細なモデルで説明されています.
ケルビンによる地球の年齢: 19世紀中頃に物理学者のケルビンが発表した地球の年齢が地質学者の常識からはあまりに若い年代だったので,大論争になったことは有名です.地球の年齢の推定にケルビンが使用した理論はこのページで扱った半無限体冷却モデルです.地球は球ですが,高温の地球が冷却する過程で生じる表面付近の熱境界層は地球半径に比較して大変薄いので,1次元の半無限体冷却モデルを適用したのは誤りではないです.ケルビンは,このモデルでは地表付近の地温勾配が時間の経過とともに小さくなることを利用して,地温勾配の観測値を理論値と比較することで年齢を決定しました.
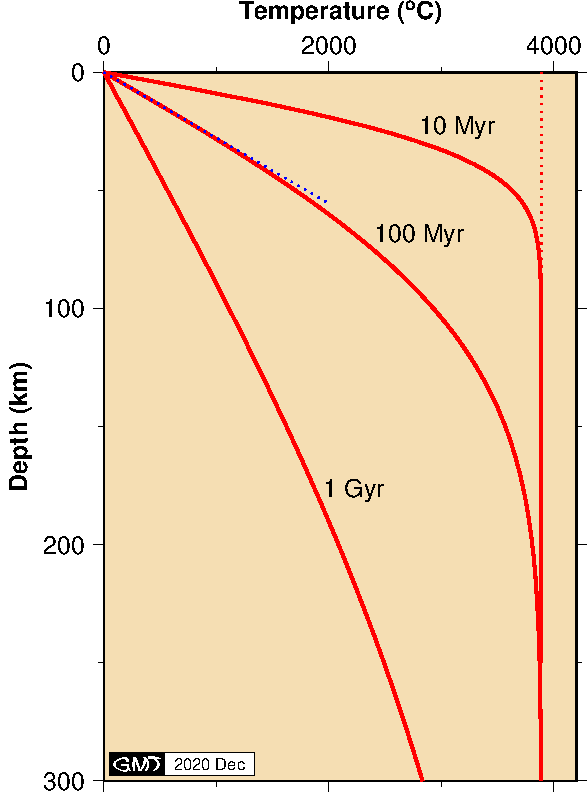
右図にケルビンが最初の論文で使用したデータ, \(T_m-T_0\) = 3888 °C, \(\kappa\) = 1.18×10-6 m2/s,による地下温度分布を3つの経過時間について示します(データは Richter (1986) より).青色の点線は当時測定された地温勾配(36 °C/km)で, 100 Myr(1億年)経過した地下温度分布とよく合います.この結果からケルビンは地球の年齢を 9800 万年とし,その後も何回か改定し,そのたびにより若い年代となり, 2400 万年を最良値としたそうです.
地球の年齢 46 億年より2桁も小さくなった原因としてよく挙げられるのが,熱源の放射性元素が考慮されていない点です.しかし, England et al. (2007) によると,モデルに熱源を加えても結果はほとんど変わらないそうです.誤りの大きな原因は,固体の地球内部も地質学的時間スケールでは対流することで,その場合には一定時間経過すると地表付近の地温勾配がある程度大きな値に保たれるそうです.
問題5-4-1
(1) 半無限体冷却モデルで,アセノスフェアの温度を \(T_m\) = 1300 °C,リソスフェアの表面と底面の温度をそれぞれ \(T_0\) = 0 °C と \(T\) = 1100 °C とします. \({\rm erf}(\eta)\) = 1100/1300 = 0.846 より \(\eta\) = 1.01 ですので,この場合のリソスフェアの厚さ \(L\) は本文の式 (10) より次式で与えられます. \[ L = 2.02\sqrt{\kappa t}. \] \(\kappa\) = 1×10-6 m2/s として,年代が (a) 10 Ma(Ma は百万年前), (b) 50 Ma, (c) 100 Ma のリソスフェアの厚さを計算しなさい.
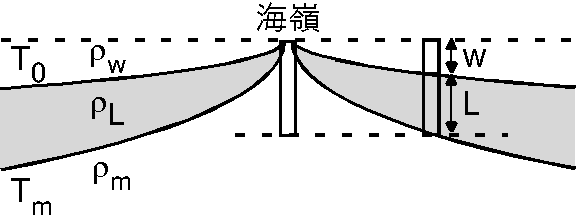
(2) 右図は海洋リソスフェアが年代とともにアイソスタシーにより沈降するモデルです.ある年代のリソスフェアの厚さを \(L\),海嶺頂上からの沈み量を \(w\),海水,リソスフェア,アセノスフェアの密度をそれぞれ \(\rho_w\), \(\rho_L\), \(\rho_m\) とします.アイソスタシーが成立するとして,沈み量を与える次式を導きなさい. \[ w = \frac{\rho_L-\rho_m}{\rho_m-\rho_w}L. \]
(3) リソスフェア内の温度分布の簡単なモデルとして,表面の \(T_0\) = 0 °C から底面の \(T_m\) まで直線的に変化しているとし,その平均値 \(\frac{1}{2}T_m\) をリソスフェアの温度とします.すると, \(\rho_L\) と \(\rho_m\) の関係は,体積膨張率 \(\alpha\) を用いて次式で表わされます. \[ \rho_L - \rho_m = {\scriptsize \frac{1}{2}}\alpha T_m\rho_m. \] いま, \(L\) = 100 km, \(\rho_m\) = 3300 kg/m3, \(\rho_w\) = 1000 kg/m3, \(T_m\) = 1300 °C, \(\alpha\) = 3.3×10-5 1/K として,リソスフェアの沈み量を計算しなさい.
【体積膨張率について】 一般に,物体は温度 \(T\) が上昇すると体積 \(v\) が増加しますが,単位温度当たりの膨張の割合を体積膨張率といい,次式で定義されます. \[ \alpha = \frac{1}{v}\frac{dv}{dT}. \] 一方,体積 \(v\) は物体の密度 \(\rho\) と質量 \(m\) に, \(v\rho=m\),の関係にあります.温度の上昇で質量が保存されるとすれば,この両辺を微分して, \(dv\rho+vd\rho=0\),から \[ \frac{dv}{v} = -\frac{d\rho}{\rho}. \] が成り立つので,体積膨張率は次のように密度を用いても表わすことができます. \[ \alpha = -\frac{1}{\rho}\frac{d\rho}{dT}. \] この問題では温度が \(T_m\) から \(\frac{1}{2}T_m\) に減少するので密度は増加します.
問題5-4-2
ケルビンが計算した方法で地球の年齢を求めてみます.本文の式 (12) を変形して,年代 \(t\) を地表の地温勾配 \(\frac{\partial T}{\partial z}|_{z=0}\) で表わす式を導きなさい.地表付近の地温勾配を 25 °C/km, \(T_m\) = 2000 °C, \(T_0\) = 0 °C, \(\kappa\) = 1×10-6 m2/s として地球の年齢を計算しなさい.
参考文献:
- England, P.C., P. Molnar, & F.M. Richter, Kelvin, Perry and the Age of the Earth, Am. Scientist, 95, 342-349, 2007.
- Richter, F.M., Kelvin and the Age of the Earth, J. Geol., 94, 395-401, 1986.
- Turcotte, D. & G. Schubert, Geodynamics (Second Edition), 456 pp., Cambridge University Press, 2002.