問題1−4−1 解答
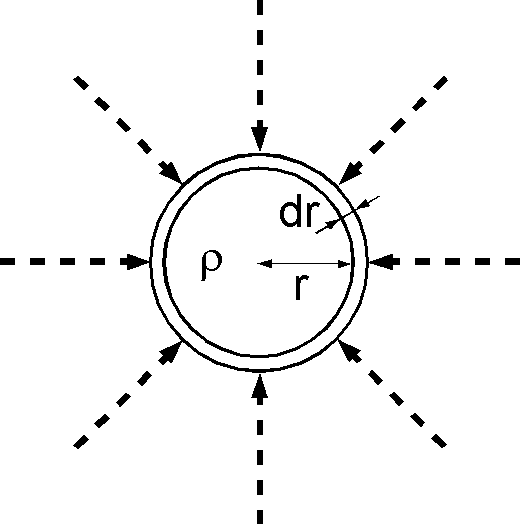
(1) 重力エネルギー \(U\) の積分は問題1-3-1で導いた式を使用して, \begin{eqnarray*} U & = & \int \frac{GM_r}{r}dm, \\ & = & \int_0^R\frac{16\pi^2 G\rho^2}{3}r^4 dr, \\ & = & \frac{16\pi^2 G\rho^2}{15}R^5 = \left(\frac{4}{3}\pi R^3\rho\right)^2\frac{9}{15}\frac{G}{R}, \\ & = & \frac{3}{5}\frac{GM^2}{R}. \end{eqnarray*}
(2) 太陽質量を計算すると,\(M = 1.991\times 10^{30}\ \mathrm{kg}\) ですので,重力エネルギーは次の値となります. \[ U = 2.279\times 10^{41}\ \mathrm{J}. \] 一方,太陽の全表面から毎秒放射されるエネルギー(太陽光度) \(L\) は太陽定数に地球軌道を半径とする球の面積を掛けて, \[ L = 3.874\times 10^{26}\ \mathrm{W\ (J/s)}, \] ですので,太陽の年令は \[ U/L = 5.883\times 10^{14}\ \mathrm{s} = 1.865\times 10^7\ \mathrm{yr}. \] よって,太陽の年令はヘルムホルツが結論した値とほぼ同じ,約 19 Myr(1900 万年)となりました.
問題1−4−2 解答
(1) ウィーンの変位則 \(\lambda_m T\) = 2900 μm K より \(T = 5800\ \mathrm{K}\).
(2) 1 m2 当たりのエネルギーである太陽定数を地球軌道半径の球の全表面について合計すると \(L = 4\pi a^2 S\).値は, \[ L = = 3.874\times 10^{26} \approx 3.9×10^{26} \ \mathrm{W}. \]
(3) \(L\) はシュテファン・ボルツマンの法則による単位面積あたりのエネルギーを,太陽の表面積について合計し, \[ L = 4\pi R^2 \sigma T^4. \] よって, \[ R = \frac{1}{T^2}\sqrt{\frac{L}{4\pi\sigma}}. \] \(R\) の値は \(6.93\times 10^8 \ \mathrm{m}\) となり,約 69 万km です(公式には 69 万 6 千km).
問題1−4−3 解答
(1) 面積速度一定の式を,楕円の面積を周期で割った値に等しいとします. \[ \frac{1}{2}r^2\frac{d\theta}{dt} = \frac{\pi ab}{T}. \] これを楕円の短半径 \(b = a\sqrt{1-e^2}\) を利用して変形します. \[ dt = \frac{T}{2\pi a^2\sqrt{1-e^2}}r^2 d\theta. \] この関係より,\(\bar I\) を求める式を \(\theta\) で積分します. \begin{align*} \bar I & = \frac{kr_0^2}{T}\int_0^T\frac{1}{r^2}dt = \frac{kr_0^2}{T}\int_0^{2\pi} \frac{T}{2\pi a^2\sqrt{1-e^2}}\frac{1}{r^2}\,r^2 d\theta \\ & = \frac{k}{2\pi\sqrt{1-e^2}}\left(\frac{r_0}{a}\right)^2\int_0^{2\pi}d\theta = k\left(\frac{r_0}{a}\right)^2\frac{1}{\sqrt{1-e^2}}. \end{align*}
(2) \(1/\sqrt{1-e^2}\) は \(e=0\) では 1,\(e=0.06\) では 1.0018 となります.よって,最も扁平な楕円軌道の場合でも,地球に入射する年平均太陽放射は約0.2%増加するだけです.
補足
高度なミランコビッチ理論から離心率起源の変動の周期は約10万年となりますが,周期の振幅は小さく,他の要因(周期約4万年の自転軸傾角や約2万年の自転軸歳差運動)の1/10以下です.しかし,過去100万年間の気温の変動の記録は10万年周期が卓越しています.この理論と観測の齟齬は最近の研究 (Abe-Ouchi et al., 2013) で解決されたようです.この研究では大気と氷床のフィードバックに加えて氷床融解後の地表の隆起の遅れなども組み入れた包括的な物理モデルを構築し,10万年周期の卓越を示しています.
参考文献:
- Abe--Ouchi et al., Insolation-driven 100,000-year glacial cycles and hysteresis of ice-sheet volume, Nature, 500, 190-194, 2013. doi: 10.1038/nature12374