物理地学の基礎：演習問題と解説

６-３ 地下電気伝導度

物質の電気の流れ易さは電気伝導度で表わされ，単位は S/m（ジーメンス・パー・メートル）です．電気伝導度の逆数が比抵抗で，単位は Ω m です．乾燥した岩石の常温での電気伝導度は 10-8~10-13 S/m で，銅の 108 S/m に比べて桁違いに小さいです．しかし，地下の電気伝導度は水の存在などで通常 10-4 S/m より大きいです．実際，前々ページで記したように，磁気嵐による地中の誘導電流が時として大規模停電の原因になるように，大地は電気をよく通します．また，地殻やマントルの電気伝導度は地球内部の温度や構成物質の推定に役立ち，地震波速度，重力，密度などとは独立した情報となっています．

地磁気の電磁誘導による方法： 地下の電気伝導度を求める方法には，例えば地面に電極を設置して電流を流すなど，幾つかあります．ここでは電離圏や磁気圏に原因する地磁気変動により地下に誘導された電流と磁場を，地表で観測することで地下電気伝導度を求める方法の基礎原理を解説します．この方法は地磁気地電流法（マグネトテルリック法, magnetotelluric method）で MT 法と呼ばれています． MT 法や地磁気による電磁感応（誘導）の詳しい解説は，学部レベルを超えますが， Constable (2007) や上嶋 (2009) にあります．

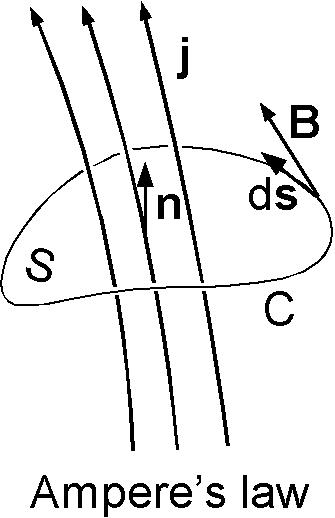
アンペールの法則

右図はアンペールの法則の説明図で， \({\bf j}\) は単位面積当たりの電流を表わす電流密度です．この法則によると，任意の閉曲線 C に沿って磁場 \({\bf B}\) を線積分すると， C で囲まれた \({\bf j}\) を面 S で面積積分した全電流に透磁率 \(\mu\) を掛けた量になります． \[ \oint{\bf B}\cdot d{\bf s} = \mu\int\int{\bf j}\cdot {\bf n}dS. \]

このアンペールの法則を右(下)図のように電気伝導度が \(\sigma\) の地中に誘導された電流と磁場に適用します．図で， x-y 面が地表で， z 軸を深さ方向に， x 軸を電流密度 \({\bf j}\) の方向にとります．すると，磁場 \({\bf B}\) は y 軸の向きとなります（次節で導きます）．

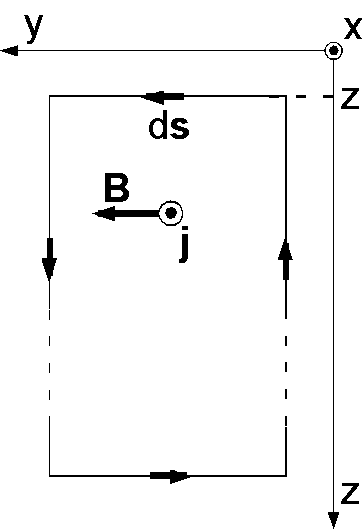
アンペールの法則の地下の誘導電場と磁場への応用

いま，電流密度を \(z\) と \(t\) の関数として，地表 \(z\) = 0 で角周波数 \(\omega\) で時間変動しているとします． \begin{equation} j(0) = e^{i\omega t}. \label{eq01} \end{equation} 以下，式の形は次節で導きますが，電流は深さとともに減衰し，位相が遅れてきます．深さ \(z\) では次式となります． \[ j(z) = e^{-z/\delta}e^{i(\omega t - z/\delta)}. \] ここに， \(\delta\) は電流の大きさが \(1/e\) に減少する深さ（スキンデプス）で， \begin{equation} \delta = \sqrt{\frac{2}{\mu\sigma\omega}}, \label{eq02} \end{equation} で表わされ，電気伝導度が大きいほど，また周期が短いほど浅い位置で電流が減少することを示します．ここで，図のように上辺と下辺が単位の長さで，縦方向に無限に長い四角形の閉曲線に沿って磁場を線積分します．その際，下辺では磁場は減衰してゼロと仮定し，左右の２辺では磁場と微小距離 \(d{\bf s}\) が垂直ですのでゼロで，結局磁場の線積分は深さ \(z\) の上辺だけが寄与し \(B(z)\) となります．これとアンペールの法則により四角形に含まれる電流密度の面積分との関係から， \begin{eqnarray*} \oint{\bf B}\cdot d{\bf s} = B(z) & = & \mu\int\int{\bf j}\cdot {\bf n}dS = \mu\int_z^\infty e^{-z/\delta}e^{i(\omega t - z/\delta)} dz, \\ & = & \mu e^{i\omega t}\int_z^\infty e^{-(z/\delta)(1+i)}dz, \\ & = & \mu e^{i\omega t}\frac{-\delta}{1+i}\left[e^{-(z/\delta)(1+i)}\right]_z^\infty, \\ & = & \frac{\mu\delta}{1+i}e^{-z/\delta}e^{i(\omega t - z/\delta)}, \\ & = & \frac{\mu\delta}{\sqrt{2}}e^{-z/\delta}e^{i(\omega t - z/\delta - \pi/4)}, \end{eqnarray*} となり，磁場の変動は電流よりも位相が 45° 遅れていることが分かります．なお，最後の式では， \[ \frac{1}{1+i} = \frac{1-i}{2} = \frac{1}{\sqrt{2}}\left[\cos\left(-\frac{\pi}{4}\right) + i\sin\left(-\frac{\pi}{4}\right)\right] = \frac{1}{\sqrt{2}}e^{-i\pi/4}, \] の変形を用いました．以上から，地表では磁場は次式で表わされます． \begin{equation} B(0) = \frac{\mu\delta}{\sqrt{2}}e^{i(\omega t - \pi/4)}. \label{eq03} \end{equation} 実際には電流密度ではなく電場 \(E\) を用い，地表で電場と磁場を測定し，その比から地下の電気伝導度を求めます．式 (1)， (2)， (3) と \(j=\sigma E\) の関係を用いて， \[ |E|/|B| = \sqrt{2}/\mu\sigma\delta = \sqrt{\omega/\mu\sigma}, \] となり，地下の電気伝導度 \(\sigma\) または比抵抗 \(\rho\) は次式で表わされます． \begin{equation} \rho = \frac{1}{\sigma} = \frac{\mu}{\omega}\left|\frac{E}{B}\right|^2. \label{eq04} \end{equation}

↑ ページ冒頭

マクスウェルの方程式からの導出： このホームページでは磁束密度 \(B\) を磁場としていますが，マクスウェルの方程式を扱うに当たっては \(H\) で表わされる磁場（または磁界）とは区別する必要があります．しかし， \(B=\mu H\) の関係を用いて，基本的には式の変形は \(B\) で表わすことにします．

電場と磁場の関係は次のマクスウェルの方程式（全ての公式は → ここにあります）で表わされます． \begin{eqnarray} \nabla\times{\bf E} & = & -\frac{\partial{\bf B}}{\partial t}, \label{eq05} \\ \nabla\times{\bf H} & = & {\bf j} + \frac{\partial{\bf D}}{\partial t}. \label{eq06} \end{eqnarray} ここで，式 (6) の変位電流 \(\partial{\bf D}/\partial t\) をゼロと近似し（理由は → ここにあります），次の関係式， \begin{eqnarray} {\bf j} & = & \sigma{\bf E}, \label{eq07} \\ {\bf B} & = & \mu{\bf H}, \label{eq08} \end{eqnarray} を用いると，式 (6) は次のようになります． \begin{equation} \nabla\times{\bf B} = \mu\sigma{\bf E}. \label{eq09} \end{equation} そこで，式 (5) と (9) から \({\bf E}\) と \({\bf B}\) の別々の方程式を導くことを考えます．

ベクトル解析の恒等式より（まとめは → ここにあります） \(\nabla\cdot(\nabla\times{\bf B})=0\) ですので式 (9) より， \begin{equation} \nabla\cdot{\bf E} = 0, \label{eq10} \end{equation} となります．また，磁荷が存在しないことから常に次式が成立します． \begin{equation} \nabla\cdot{\bf B} = 0, \label{eq11} \end{equation} 式 (5) の両辺に \(\nabla\) をベクトル積で作用させ（rot を作用），恒等式を用いると， \[ \nabla\times(\nabla\times{\bf E}) = \nabla(\nabla\cdot{\bf E}) - \nabla^2{\bf E} = -\frac{\partial}{\partial t}(\nabla\times{\bf B}), \] となり，式 (10) から左辺第１項はゼロで，右辺は式 (9) を用いて \({\bf E}\) で表わすと次式を得ます． \begin{equation} \nabla^2{\bf E} = \mu\sigma\frac{\partial{\bf E}}{\partial t}. \label{eq12} \end{equation} 同様にして，式 (9) から， \[ \nabla\times(\nabla\times{\bf B}) = \nabla(\nabla\cdot{\bf B}) - \nabla^2{\bf B} = \mu\sigma\nabla\times{\bf E}, \] となり，左辺の第１項は式 (11) からゼロ，右辺は式 (5) を用いて \({\bf B}\) で表わすと次式となります． \begin{equation} \nabla^2{\bf B} = \mu\sigma\frac{\partial{\bf B}}{\partial t}. \label{eq13} \end{equation} 式 (12) と (13) から \({\bf E}\) と \({\bf B}\) は同じ形の別々の方程式を満たすことになります．この方程式は「→ ５ 地球の熱と温度」で扱った拡散方程式です．

↑ ページ冒頭

ここで，地表を原点として深さ方向に z 軸をとり，電場も磁場も \({\bf E}(z,t)\)， \({\bf B}(z,t)\) のように \(z\) と \(t\) だけの関数とします．すると， \(x\) と \(y\) での偏微分はゼロとなりますので，微分演算子の公式を用いて（まとめは → ここにあります），式 (5) と (9) を成分で表わすと次の関係式が得られます． \begin{eqnarray} \left(-\frac{\partial E_y}{\partial z}, \frac{\partial E_x}{\partial z}, 0\right) & = & \left(-\frac{\partial B_x}{\partial t}, -\frac{\partial B_y}{\partial t}, -\frac{\partial B_z}{\partial t}\right), \label{eq14} \\ \left(-\frac{\partial B_y}{\partial z}, \frac{\partial B_x}{\partial z}, 0\right) & = & \mu\sigma(E_x, E_y, E_z). \label{eq15} \end{eqnarray} 式 (15) から \(E_z\) はゼロとなります． \[ E_z = 0. \] 式 (14) 及び式 (11) から， \[ \frac{\partial B_z}{\partial t} = \frac{\partial B_z}{\partial z} = 0, \] となり， \(B_z\) は \(t\) と \(z\) に対して一定ですが，変動部分だけを考えれば良いので \(B_z\) もゼロとします． \[ B_z = 0. \] ここで， \({\bf E}\) の方向に x 軸を取ることにすると， \(E_y\) はゼロです． \[ E_y = 0. \] すると，式 (14) と (15) から， \[ \frac{\partial B_x}{\partial t} = \frac{\partial B_x}{\partial z} = 0, \] となり， \(B_x\) もゼロとします． \[ B_x = 0. \] 以上から，水平面内にある電場と磁場は直交していて，成分の添字は省略し，次のように表わせます． \begin{eqnarray} {\bf E} & = & (E, 0 ,0), \label{eq16} \\ {\bf B} & = & (0, B, 0). \label{eq17} \end{eqnarray} また，式 (14) と (15) から， \(E\) と \(B\) には次の関係があります． \begin{eqnarray} \frac{\partial E}{\partial z} & = & -\frac{\partial B}{\partial t}, \label{eq18} \\ \mu\sigma E & = & -\frac{\partial B}{\partial z}. \label{eq19} \end{eqnarray}

↑ ページ冒頭

改めて式 (12) と (13) を成分で表わすと次の２つの方程式となります． \begin{eqnarray} \frac{\partial^2 E}{\partial z^2} & = & \mu\sigma\frac{\partial E}{\partial t}, \label{eq20} \\ \frac{\partial^2 B}{\partial z^2} & = & \mu\sigma\frac{\partial B}{\partial t}, \label{eq21} \end{eqnarray} この方程式の解は「→ ５-３ 時間周期...非定常熱伝導方程式」で扱った熱拡散方程式の熱拡散率 \(\kappa\) を \(1/\mu\sigma\) で置き換えた形になり，冒頭の式 (2) と重複しますがスキンデプス， \begin{equation} \delta = \sqrt{\frac{2}{\mu\sigma\omega}}, \label{eq22} \end{equation} を用いて，次のように表わせます． \begin{eqnarray} E(z) & = & E_0e^{-z/\delta}e^{i(\omega t - z/\delta)}, \label{eq23} \\ B(z) & = & B_0e^{-z/\delta}e^{i(\omega t - z/\delta)}. \label{eq24} \end{eqnarray} ここで，電場の変動によって磁場の変動が現れると考え， \(B_0\) を \(E_0\) で表わします．式 (23) と (24) を式 (19)（又は(18)）に代入して， \[ \mu\sigma E_0e^{-z/\delta}e^{i(\omega t - z/\delta)} = \frac{1+i}{\delta}B_0e^{-z/\delta}e^{i(\omega t - z/\delta)}. \] 式 (22) の \(\delta\) を代入し，冒頭に示した \(\sqrt{2}/(1+i) = e^{-i\pi/4}\) を用いて整理すると， \[ B_0 = \delta\mu\sigma\frac{1}{1+i}E_0 = \sqrt{\frac{\mu\sigma}{\omega}}\frac{\sqrt{2}}{1+i}E_0 = \sqrt{\frac{\mu\sigma}{\omega}}e^{-i\pi/4}E_0. \] 簡単のために \(E_0\) = 1 とすると，式 (23) と (24) は， \begin{eqnarray} E(z) & = & e^{-z/\delta}e^{i(\omega t - z/\delta)}, \label{eq25} \\ B(z) & = & \sqrt{\frac{\mu\sigma}{\omega}}e^{-z/\delta}e^{i(\omega t - z/\delta - \pi/4)}. \label{eq26} \end{eqnarray} となり， \(z\) に対する減衰の割合は \(E\) も \(B\) も同じですが， \(B\) の位相が 45° 遅れていることが分かります．この２つの式から，地表（\(z\) = 0）で測定した電場と磁束密度の大きさの比から，冒頭の式 (4) と同じですが，地下の電気伝導度 \(\sigma\) 又は比抵抗 \(\rho\) を決定する次式が導かれます． \begin{equation} \rho = \frac{1}{\sigma} = \frac{\mu}{\omega}\left|\frac{E}{B}\right|^2. \label{eq27} \end{equation}

以上の MT 法の解説はあくまで基礎原理です．実際の観測では，地下の電気伝導度が一様ではなく，複数の層構造など複雑な地下構造を仮定します．また，通常は電場や磁場の時間に対する記録を周波数に分解して周波数解析を行うようです． MT 法などの地磁気の電磁誘導による方法は，活断層や火山から地殻深部やマントルまでの電気伝導度構造の解明に応用されています．

なお，学部の電磁気学で最後に学ぶ真空中の電磁波の導出は上記の方法とは違い，マクスウェルの方程式を電流密度と電荷密度をゼロとして解きます．そのため，次のような波動方程式となります． \[ \nabla^2{\bf E} = \varepsilon_0\mu_0\frac{\partial^2{\bf E}}{\partial t^2}, \quad \nabla^2{\bf B} = \varepsilon_0\mu_0\frac{\partial^2{\bf B}}{\partial t^2}. \]

↑ ページ冒頭

問題６-３-１

（１） 地磁気は外核内のダイナモ作用により発生してますが，その変動は核表面ではあらゆる周期成分を含むと考えられています（ホワイトスペクトル）．しかし，周期の短い信号はマントルや地殻を通過する間に電磁的に減衰して地表まで届きません．そこで，コア起源の地磁気変動のうち，地表で観測される最短の周期を１年とし，その信号が地表では \(1/e\) に減衰しているとします．マントルと地殻を平坦な層構造として，その見掛けの電気伝導度を見積もりなさい．但し，透磁率は真空の値 \(\mu_0\) = 4π×10-7 N/A2 とし，コア・マントル境界の深さを 2900 km とします．

（２） 磁気嵐中の地磁気変動を地表で観測したところ，電場と磁場の変化の大きさはそれぞれ 100 mV/km と 250 nT で周期は 1 h であった．本文の MT 法の基礎理論に従って，地下の比抵抗，電気伝導度，およびスキンデプスを計算しなさい．

→ 問題６-３-１ 解説

参考文献：

↑ ページ冒頭   ← 前ページ   → 次ページ