 統計学的検定:分布の検定; histo と histo2
統計学的検定:分布の検定; histo と histo2
科学のどの分野においても,あるデータが正規(ガウス)分布のような理論分布に従っているかどうかを知ることは重要です.また,2つのデータの分布が異なるかどうかを知ることもしばしば必要です.これらの問題を解くための効果的で容易な方法は,データのヒストグラムを描いて統計的検定を行うことです.プログラム "histo" と "histo2" はこのための手段を提供します.
このような目的では,帰無仮説は「H: 観測されたデータは正規分布の母集団からのものである」や「H: 2つのデータの分布は同じ母集団からの分布である」となるでしょう.ここで重要なことは,統計的検定の目的はこれらの帰無仮説を否定することです.それ故,帰無仮説が棄却されなかったときには,帰無仮説が正しいと主張することはできません.即ち,「データは正規分布である」や「2つのデータの分布は同じである」と主張するのは誤りで,「データは正規分布とは矛盾しない」や「2つのデータの分布は1つの分布と矛盾しない」と述べるに留めます.
プログラム "histo" はあるデータの分布が正規分布と対数正規分布のどちらに近いかの統計的検定を,カイ二乗検定とコルモゴロフ-スミルノフ検定を使用して行います.カイ二乗検定では,階級の区分けをそれぞれの階級のデータ数ができるだけ等しくなるように設定します.このためには階級の境界を,データの平均と標準偏差による正規(対数正規)分布の確率密度が等分されるように決定します.カイ二乗検定は階級数が 4 から順次階級数を増やして繰り返され,各階級における仮定した分布の期待値が 5 より小さくなると終了します.
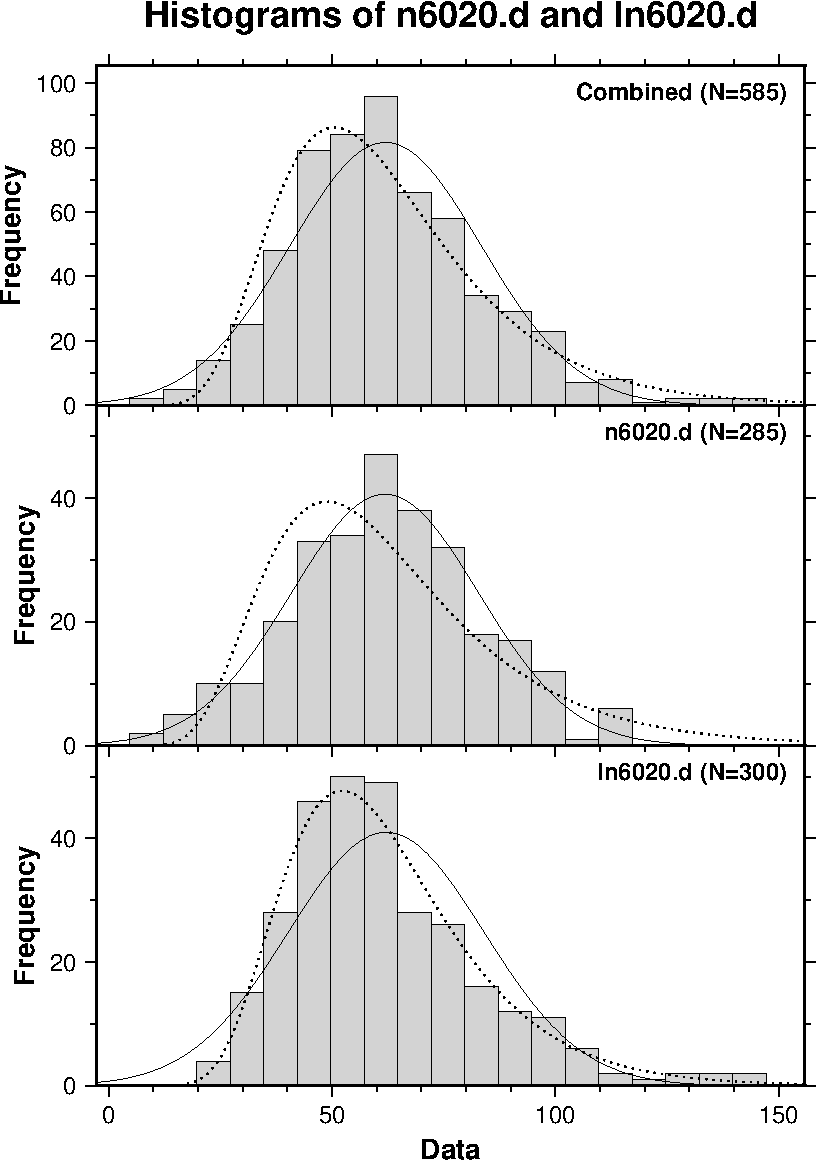
プログラム "histo2" は2つのデータ・ファイルを読み込み,2データの分布が異なるかどうかの統計的検定をカイ二乗検定とコロモゴロフ-スミルノフ検定により実施します.カイ二乗検定では,階級の境界は2データの合計の累積分布を等分するように決定します.カイ二乗検定は, "histo" と同様に,異なる階級数で繰り返されます.プログラム "histo2" はまた,それぞれのデータについて正規(対数正規)分布に対する検定も実施します.下図は "histo2" によりプロットしたヒストグラムの例で,正規分布と対数正規分布に従う乱数によるデータの分布を比較しています.統計的検定の結果は stdout (Linux 端末)へ出力されます.
カイ二乗検定
カイ二乗(\(\chi^2\))検定はデータをヒストグラムで表し,各階級のデータ度数と,比較する分布の期待度数との差の程度を測定します.階級数を \(N_B\) とすると,カイ二乗統計量は次式で表されます. \begin{equation} \chi^2 = \sum_{i=1}^{N_B}\frac{(n_i - e_i)^2}{e_i}, \label{eq01} \end{equation} ここに, \(n_i\) は \(i\) 番目の階級におけるデータ度数で, \(e_i\) は比較する分布による期待値です.この統計量は, \(N_B\) ≥ 5 で \(e_i\) ≥ 5 の場合に,自由度が \(\nu=N_B-1\) のカイ二乗分布でよく近似されることが知られています(ホーエル, 1978).観測された \(\chi^2\) が有意水準 \(\alpha\) に対応する一定の値を越えれば,データが仮定した分布からの標本であるという帰無仮説は棄却されます.比較する分布が,データから決定した平均と標準偏差による正規(対数正規)分布の場合には,自由度は使用した母数の数だけ減少します.よって,このような場合には,自由度は \(\nu = N_B-3\) となります.
カイ二乗検定は2つのデータの分布が異なるかどうかの検定にも適用されます.いま, \(R_i\) と \(S_i\) をそれぞれデータ1とデータ2の同じ \(i\) 番目の階級のデータ度数とします.カイ二乗統計量は, \begin{equation} \chi^2 = \sum_{i=1}^{N_B}\frac{(\sqrt{S/R}R_i - \sqrt{R/S}S_i)^2}{R_i + S_i}, \label{eq02} \end{equation} で与えられ,ここに \(R\) はデータ1の, \(S\) はデータ2の総度数です(Press et al., 1992).式 \eqref{eq02} の統計量は自由度が \(\nu=N_B-1\) の \(\chi^2\) 分布に従います.
コロモゴロフ-スミルノフ検定
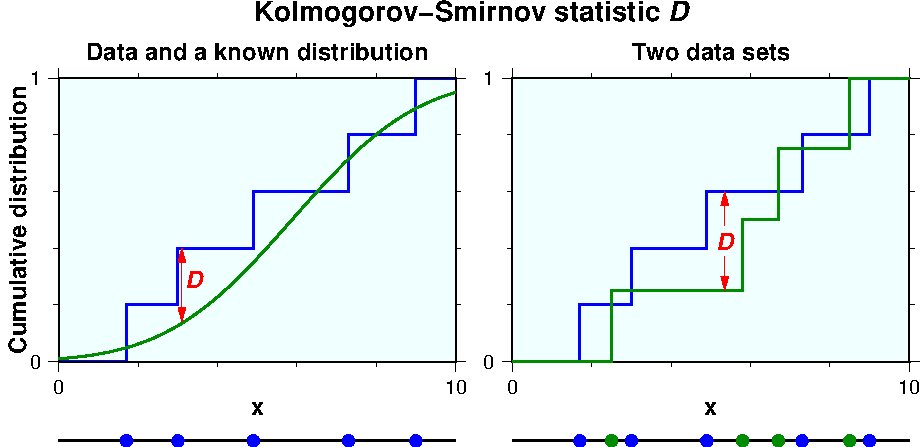
コロモゴロフ-スミルノフ(Kolmogorov-Smirnov, K-S)検定は,観測されたデータの累積分布曲線を他の観測データ(または理論分布)のそれと比較し,それらの差の程度を測定します.その差が大きいほど2つの分布が異なる確率は高いと考えられます.いま,昇順にソートされた \(N\) 個のデータ \(x_i (i=1 \cdots N)\) を考えます. K-S 検定では,データの累積分布関数 \(S_N(x)\) は次の階段関数で表されます. \begin{equation} S_N(x) = \left\lbrace \begin{array}{cl} 0 & (x < x_1), \\ i/N & (x_i ≤ x < x_{i+1}), \label{eq03} \\ 1 & (x ≥ x_N). \end{array} \right. \end{equation} 1つのデータ分布を理論分布と比較するときは, K-S 統計量はデータと理論分布の累積分布曲線, \(S_N(x)\) と \(F(x)\),の差の絶対値の最大値です; \begin{equation} D = \max_{-\infty< x <\infty} |S_N(x) - F(x)|. \label{eq04} \end{equation} 2つのデータの分布を比較するときは, K-S 統計量 \(D\) は, \begin{equation} D = \max_{-\infty< x <\infty} |S_{N_1}(x) - S_{N_2}(x)|, \label{eq05} \end{equation} となり,ここに \(S_{N_1}(x)\) と \(S_{N_2}(x)\) はそれぞれデータ1とデータ2の累積分布関数です.下図は K-S 統計量 \(D\) の模式図で,観測データが理論分布(左図)や他のデータ(右図)と比較される様子を示します.
観測された統計量 \(D_{obs.}\) から,有意確率 \(P\) を見積もる方法には幾つかあります(有意確率とは帰無仮説が正しいときに観測された統計量を得る確率で,有意水準 \(\alpha\) より小さいと帰無仮説は棄却されます).ここでは, Press et al. (1992) に従い,次式で与えられる \(Q_{KS}\), \begin{equation} Q_{KS}(\lambda) = 2\sum_{j=1}^\infty (-1)^{j-1} e^{-2j^2\lambda^2}. \label{eq06} \end{equation} を使用して, \(P\) は次式で与えられます. \begin{equation} P(D>D_{obs.}) = Q_{KS}\left(\left[\sqrt{N_e} + 0.12 + 0.11\left/\sqrt{N_e}\right.\right]D_{obs.}\right), \label{eq07} \end{equation} ここに, \(N_e\) は有効データ数; \begin{equation} N_e = N, \label{eq08} \end{equation} は \eqref{eq04} によるデータと理論分布の場合, \begin{equation} N_e = \frac{N_1 N_2}{N_1 + N_2}, \label{eq09} \end{equation} は \eqref{eq05} による2つのデータの場合です.式 \eqref{eq07} の正確さは \(N_e\) が大きいほど増しますが, Press et al (1992) によると \(N_e \geq 4\) のような小さなデータ数でも十分に正確のようです.しかしこのことはプログラム "histo" や "histo2" で,データと正規(対数正規)分布を比較する場合には必ずしも正しくないことを指摘しておきます.それは,プログラムがデータから求めた2つの母数,平均と標準偏差,を使用するからです.このような場合には, Press et al. (1992) はシミュレーションによる方法を推奨してますが, "histo" と "histo2" では行っていません.
プログラムのダウンロードとインストール
正規,対数正規, \(\chi^2\) 分布に関する関数の概要
以下, \(f(x)\) と \(F(x)\) はそれぞれ \(x\) の確率密度と累積分布で, \(P(x_c)\) は \(x\) が基準値 \(x_c\) を超える確率です.定義や表記は次のマニュアルや教科書を参考にしています: Crow et al. (1960),小針 (1973), Press et al. (1992).
正規分布:
\begin{equation} f(x) = {1 \over \sqrt{2\pi}\sigma}e^{-(x-\mu)^2/2\sigma^2}. \label{eq10} \end{equation} ここに, \(\mu\) と \(\sigma^2\) は \(x\) の平均と分散です.標準化した変数, \begin{equation} z = (x - \mu)/\sigma, \label{eq11} \end{equation} を導入すると, \(z\) の確率密度関数は次式で与えられます. \begin{equation} f(z) = {1 \over \sqrt{2\pi}}e^{-z^2/2}. \label{eq12} \end{equation} \(f(z)\) の不定積分は初等関数では表せないので, \(\int_{-\infty}^\infty f(z)=1\) を示すことは困難です.しかし,以下のような方法で導くことはできます(数学的には厳密ではないかもしれません).次の二重積分を考えます. \[ \int_{-\infty}^\infty e^{-u^2/2}du \int_{-\infty}^\infty e^{-v^2/2}dv = \int_{-\infty}^\infty\int_{-\infty}^\infty e^{-(u^2 + v^2)/2}du dv. \] 次のように \(r\) と \(\theta\) を導入します. \[ u = r\cos\theta, \quad v = r\sin\theta, \quad dudv = r dr d\theta, \] 二重積分は以下のように求まります. \[ \int_0^{2\pi}d\theta\int_0^\infty r e^{-r^2/2}dr = 2\pi\left[-e^{-r^2/2}\right]_0^\infty = 2\pi. \] よって, \(\int_{-\infty}^\infty e^{-z^2/2}dz=\sqrt{2\pi}\),即ち \(\int_{-\infty}^\infty f(z)=1\).
式 \eqref{eq12} を使用して \(x\) の平均と分散は以下のように求まります. \begin{eqnarray*} E[x] & = & {1 \over \sqrt{2\pi}\sigma}\int_{-\infty}^\infty x e^{-(x-\mu)^2/2\sigma^2}dx, \\ & = & {1 \over \sqrt{2\pi}}\int_{-\infty}^\infty(\sigma z + \mu) e^{-z^2/2}dz, \\ & = & {\sigma \over \sqrt{2\pi}}\left[-e^{-z^2/2}\right]_{-\infty}^\infty + {\mu \over \sqrt{2\pi}}\int_{-\infty}^\infty e^{-z^2/2}dz = \mu. \end{eqnarray*} \begin{eqnarray*} E[(x-\bar x)^2] & = & {1 \over \sqrt{2\pi}\sigma}\int_{-\infty}^\infty (x-\mu)^2 e^{-(x-\mu)^2/2\sigma^2}dx, \\ & = & {\sigma^2 \over \sqrt{2\pi}}\int_{-\infty}^\infty z^2 e^{-z^2/2}dz = {\sigma^2 \over \sqrt{2\pi}}\int_{-\infty}^\infty z\left(-e^{-z^2/2}\right)^{'} dz, \\ & = & {\sigma^2 \over \sqrt{2\pi}}\left[-ze^{-z^2/2}\right]_{-\infty}^\infty + {\sigma^2 \over \sqrt{2\pi}}\int_{-\infty}^\infty e^{-z^2/2}dz = \sigma^2. \end{eqnarray*} 最後の式の変形では,部分積分を使用し最初の項は証明なしでゼロとしました(\(\int_{-\infty}^\infty z^2 e^{-z^2/2}dz=\sqrt{2\pi}\) は数学公式集にも載っています).
\(\def\erf{\mathop{\mathrm{erf}}\nolimits}\) \(\def\erfc{\mathop{\mathrm{erfc}}\nolimits}\) 積分 \(\int_{-\infty}^x f(x)dx\) は初等関数で表せないので,累積分布 \(F(x)\) を表すためには誤差関数 \(\erf(x)\) と相補誤差関数 \(\erfc(x)\) を導入します; \begin{eqnarray} \erf(x) & = & {2 \over \sqrt{\pi}}\int_0^x e^{-t^2}dt, \label{eq13} \\ \erfc(x) & = & 1 - \erf(x) = {2 \over \sqrt{\pi}}\int_x^\infty e^{-t^2}dt, \label{eq14} \end{eqnarray} \(z ≥ 0\) のときは, \eqref{eq12} を使用し \(t=z/\sqrt{2}\) と置いて, \begin{eqnarray*} F(z) & = & {1 \over \sqrt{2\pi}}\int_{-\infty}^z e^{-z^2/2} dz, \\ & = & 0.5 + {1 \over \sqrt{2\pi}}\int_0^z e^{-z^2/2} dz = 0.5 + {1 \over \sqrt{\pi}}\int_0^{z/\sqrt{2}} e^{-t^2} dt, \\ & = & 0.5 + {1 \over 2}\erf\left({z \over \sqrt{2}}\right). \end{eqnarray*} 同様にして \(z < 0\) の場合も, \begin{eqnarray*} F(z) & = & 1 - {1 \over \sqrt{2\pi}}\int_z^\infty e^{-z^2/2} dz, \\ & = & 1 - {1 \over \sqrt{\pi}}\int_{z/\sqrt{2}}^\infty e^{-t^2} dt = 1 - {1 \over 2}\erfc\left({z \over \sqrt{2}}\right), \\ & = & 0.5 + {1 \over 2}\erf\left({z \over \sqrt{2}}\right). \end{eqnarray*} これらを統合して, \(z\) と \(x\) の全ての範囲に対して累積分布は次式で与えられます. \begin{eqnarray} F(z) & = & 0.5 + {1 \over 2}\erf\left({z \over \sqrt{2}}\right), \label{eq15} \\ F(x) & = & 0.5 + {1 \over 2}\erf\left(\frac{x-\mu}{\sqrt{2}\sigma}\right). \label{eq16} \end{eqnarray}
\(z\) が基準値 \(z_c\) を超える確率 \(P(z_c)\) は, \eqref{eq15} を \(P(z_c)= 1-F(z_c)\) に代入することで得られます(\(x\) についても同様です). \begin{eqnarray} P(z_c) & = & {1 \over 2}\erfc\left({z_c \over \sqrt{2}}\right), \label{eq17} \\ P(x_c) & = & {1 \over 2}\erfc\left(\frac{x_c-\mu}{\sqrt{2}\sigma}\right). \label{eq18} \end{eqnarray}
対数正規分布:
対数正規分布は \(y=\log x\) が正規分布に従うときの \(x\) の分布です.いま, \(y\) の確率密度 \(g(y)\) を, \begin{equation} g(y) = {1 \over \sqrt{2\pi}\sigma}e^{-(y-\mu)^2/2\sigma^2}, \label{eq19} \end{equation} とします.ここに, \begin{equation} y = \log x \quad (x > 0), \label{eq20} \end{equation} です.この場合, \(x=e^y\) の確率密度 \(f(x)\) は次式を満たします. \[ g(y)dy = f(x)dx. \] よって, \begin{eqnarray} f(x) & = & g(y){dy \over dx} = g(\log x){1 \over x}, \nonumber \\ & = & {1 \over \sqrt{2\pi}\sigma x}e^{-(\log x-\mu)^2/2\sigma^2} \quad (x > 0), \label{eq21} \end{eqnarray} となります.また, \(\int_0^\infty f(x) = 1\) は明らかです.
\(x\) の平均は以下のようにして導かれます. \[ E[x] = \int_0^\infty xf(x)dx = {1 \over \sqrt{2\pi}\sigma}\int_0^\infty e^{-(\log x-\mu)^2/2\sigma^2}dx. \] \(t=\log x\) と置くと \(dx=e^t dt\) ですので, \begin{eqnarray} E[x] & = & {1 \over \sqrt{2\pi}\sigma}\int_{-\infty}^\infty e^{-(t-\mu)^2/2\sigma^2+t}dt, \nonumber \\ & = & e^{(2\mu+\sigma^2)/2}{1 \over \sqrt{2\pi}\sigma}\int_{-\infty}^\infty e^{-(t-(\mu+\sigma^2))^2/2\sigma^2}dt, \nonumber \\ & = & e^{\mu+\sigma^2/2}. \label{eq22} \end{eqnarray} \(x\) の分散を導くには,最初に \(E[x^2]\) を求めます. \begin{eqnarray*} E[x^2] & = & \int_0^\infty x^2f(x)dx = {1 \over \sqrt{2\pi}\sigma}\int_0^\infty x e^{-(\log x-\mu)^2/2\sigma^2}dx, \\ & = & {1 \over \sqrt{2\pi}\sigma}\int_{-\infty}^\infty e^{t-(t-\mu)^2/2\sigma^2+t}dt, \\ & = & e^{2(\mu+\sigma^2)}{1 \over \sqrt{2\pi}\sigma}\int_{-\infty}^\infty e^{-(t-(\mu+2\sigma^2))^2/2\sigma^2}dt, \\ & = & e^{2(\mu+\sigma^2)}. \end{eqnarray*} よって, \(x\) の分散は次式で与えられます. \begin{eqnarray} E[(x-\bar x)^2] & = & E[x^2] - {\bar x}^2, \nonumber \\ & = & e^{2(\mu+\sigma^2)} - e^{2\mu+\sigma^2}, \nonumber \\ & = & e^{2\mu+\sigma^2}(e^{\sigma^2}-1). \label{eq23} \end{eqnarray}
対数正規分布の累積分布関数 \(F(x)\) は以下のように表されます. \[ F(x) = {1 \over \sqrt{2\pi}\sigma}\int_0^x {1 \over x}e^{-(\log x-\mu)^2/2\sigma^2}dx. \] \(t=-(\log x-\mu)/\sqrt{2}\sigma\) と置き, \(dx=-\sqrt{2}\sigma x dt\) を使用して, \begin{eqnarray} F(x) & = & -{1 \over \sqrt{\pi}}\int_\infty^{-(\log x-\mu)/\sqrt{2}\sigma}e^{-t^2}dt, \nonumber \\ & = & {1 \over \sqrt{\pi}}\int_{-(\log x-\mu)/\sqrt{2}\sigma}^\infty e^{-t^2}dt, \nonumber \\ & = & {1 \over 2}\erfc\left(-\frac{\log x-\mu}{\sqrt{2}\sigma}\right). \label{eq24} \end{eqnarray}
\(x\) が基準値 \(x_c\) を超える確率 \(P(x_c)=1-F(x_c)\) は次式となります. \begin{equation} P(x_c) = 1 - {1 \over 2}\erfc\left(-\frac{\log x_c-\mu}{\sqrt{2}\sigma}\right) = 0.5 + {1 \over 2}\erf\left(-\frac{\log x_c-\mu}{\sqrt{2}\sigma}\right). \label{eq25} \end{equation}
\(\chi^2\) 分布:
\begin{equation} f(x) = \frac{1}{2^{\nu \over 2}\Gamma\left({\nu \over 2}\right)}x^{{\nu \over 2}-1}e^{-{x \over 2}} \quad (x > 0). \label{eq26} \end{equation} 累積分布 \(F(x)\) を表すには次の不完全ガンマ関数を使用します. \begin{eqnarray*} \gamma(a,x) & = & \int_0^x t^{a-1}e^{-t}dt, \\ \Gamma(a,x) & = & \int_x^\infty t^{a-1}e^{-t}dt = \Gamma(a) - \gamma(a,x). \end{eqnarray*} 式 \eqref{eq26} を積分して, \[ F(x) = \frac{1}{2^{\nu \over 2}\Gamma\left({\nu \over 2}\right)}\int_0^x x^{{\nu \over 2}-1}e^{-{x \over 2}}dx. \] \(t=x/2\) と置き,よって \(dx=2dt\) を使用して, \begin{eqnarray} F(x) & = & \frac{1}{2^{\nu \over 2}\Gamma\left({\nu \over 2}\right)}\int_0^t 2^{{\nu \over 2}-1}t^{{\nu \over 2}-1}e^{-t}2dt, \nonumber \\ & = & \frac{1}{\Gamma\left({\nu \over 2}\right)}\int_0^{x/2}t^{{\nu \over 2}-1}e^{-t}dt, \nonumber \\ & = & \frac{\gamma\left({\nu \over 2},{x \over 2}\right)}{\Gamma\left({\nu \over 2}\right)}. \label{eq27} \end{eqnarray} 同様にして, \(P(x_c)=1-F(x_c)\) は次式で与えられます. \begin{equation} P(x_c) = \frac{\Gamma\left({\nu \over 2},{x \over 2}\right)}{\Gamma\left({\nu \over 2}\right)}. \label{eq28} \end{equation}
参考文献:
- Crow, E. L., F. A. Davis, and M. W. Maxfield, Statistics Manual, 288 pp., Dover Pub. Inc., New York, 1960.
- ホーエル, P. G., 入門数理統計学, 404 pp., 培風館, 東京, 1978.
- 小針アキ宏, 確率・統計入門, 300 pp., 岩波書店, 東京, 1973.
- Press, W.H., S.A. Teukolsky, W.T. Vetterling, and B.P. Flannery, Numerical Recipes in C: The Art of Scientific Computing (Second Edition), 994 pp., Cambridge University Press, Cambridge, 1992.