４-４ 弾性体の力学と断層運動
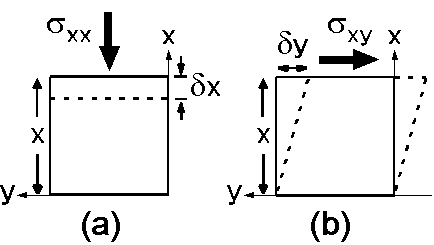
応力と歪み： 応力と歪については「→ ４-２ 地震波の伝播」でも触れましたが，以下はより詳しいまとめです．応力とは物体内部で作用する単位面積あたりの力で，ある面に垂直な成分を法線応力，平行な成分をずれ応力（せん断応力）といいます．応力は \(\sigma_{xx}\) などと記しますが，１番目の添え字は応力が働く面を，２番目は応力の方向を表わします．例えば \(\sigma_{xx}\) は \(x\) の面で \(-x\) 方向に働く応力で，通常の圧力と同じと考えて構いません．ここに， \(x\) 面とは \(x\) 軸に垂直な面で，面に立てた外向き法線が \(+x\) 軸方向の場合を正の \(x\) 面， \(-x\) 軸方向の場合を負の \(x\) 面といいます．そして，正の面では負方向の応力を正，負の面では正方向の応力を正とします．これは地球内部を扱う場合の定義で，一般の応力ベクトルの正負の定義とは逆ですので注意が必要です．また， \(\sigma_{xy}\) は \(x\) の面に沿って \(-y\) 方向に働く応力で，物体を横方向にずらすような力と考えてよいです．応力の単位は圧力と同じ Pa（パスカル）で， 1 Pa = 1 N/m2 です．大気圧を Pa で表わすと， 1 atm = 約 0.1 MPa = 約 1013 hPa です（M はメガで 106， h はヘクトで 102です）．
一方，歪みとは物体の変形の程度を表す量で，変形前の値で規格化して割合に直します．弾性体では，歪みは応力に比例し，これをフックの法則といいいます．図（a）のように，高さ \(x\) の弾性体ブロックが法線応力 \(\sigma_{xx}\) により \(\delta x\) 短縮した場合の歪みを伸縮歪みといい， \begin{equation} \epsilon_{xx} = \frac{\delta x}{x}, \label{eq01} \end{equation} で表され，地球科学分野では短縮する場合を正とします．フックの法則は， \begin{equation} \sigma_{xx} = E \epsilon_{xx}, \label{eq02} \end{equation} で与えられ， \(E\) はヤング率です．図（b）のようなずれ応力が働いた場合の横方向の歪みをずれ歪み（せん断歪み）といい， \begin{equation} \epsilon_{xy} = \frac{1}{2}\frac{\delta y}{x}, \label{eq03} \end{equation} で表されます．但し，これは単純ずれ歪みの場合で，一般的には \(\epsilon_{xy}=(1/2)(\delta y/x+\delta x/y)\) で定義されます．ここでは (3) の定義に従い，この場合のフックの法則は， \begin{equation} \sigma_{xy} = 2 \mu \epsilon_{xy}, \label{eq04} \end{equation} となり， \(\mu\) を剛性率といいます．
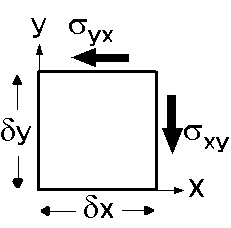
３次元弾性体： 一般化された３次元弾性体では， \(\sigma_{xx}\)， \(\sigma_{xy}\)， \(\sigma_{xz}\)， \(\sigma_{yx}\)， \(\sigma_{yy}\)， \(\sigma_{yz}\)， \(\sigma_{zx}\)， \(\sigma_{zy}\)， \(\sigma_{zz}\) の９個の変数が必要です．しかし， \(\sigma_{xy}\) = \(\sigma_{yx}\)， \(\sigma_{xz}\) = \(\sigma_{zx}\)， \(\sigma_{yz}\) = \(\sigma_{zy}\) の対称性のために，実際には６個の変数で記述します（歪みについても同様）．この対称性は，図で \(z\) 軸（紙面に垂直）の回りの力のモーメントがつり合うことから得られます．図の微小な直方体が回転しないためには， \[ (\sigma_{xy}\times\delta y)\times\delta x = (\sigma_{yx}\times\delta x)\times\delta y, \] が成り立つ必要があり，これより， \[ \sigma_{xy} = \sigma_{yx}, \] が得られ，他も同様です．一般化されたフックの法則は大変複雑で，次式で表されます． \begin{eqnarray} \sigma_{xx} & = & (\lambda+2\mu)\epsilon_{xx} + \lambda\epsilon_{yy} + \lambda\epsilon_{zz}, \nonumber \\ \sigma_{yy} & = & \lambda\epsilon_{xx} + (\lambda+2\mu)\epsilon_{yy} + \lambda\epsilon_{zz}, \nonumber \\ \sigma_{zz} & = & \lambda\epsilon_{xx} + \lambda\epsilon_{yy} + (\lambda+2\mu)\epsilon_{zz}, \label{eq05} \\ \sigma_{xy} & = & 2\mu\epsilon_{xy}, \nonumber \\ \sigma_{xz} & = & 2\mu\epsilon_{xz}, \nonumber \\ \sigma_{yz} & = & 2\mu\epsilon_{yz}. \nonumber \end{eqnarray} ここに \(\lambda\) と \(\mu\) はラメの定数といわれます（\(\mu\) は前述の剛性率）．これらの式を解析すると，例えば \(x\) 方向に圧縮応力 \(\sigma_{xx}\) が働くと \(x\) 方向に縮むだけでなく， \(y\) と \(z\) 方向にも膨らむことが導かれます．しかし，ここでは基礎レベルとして，これらの式の詳細な扱いは省略します．
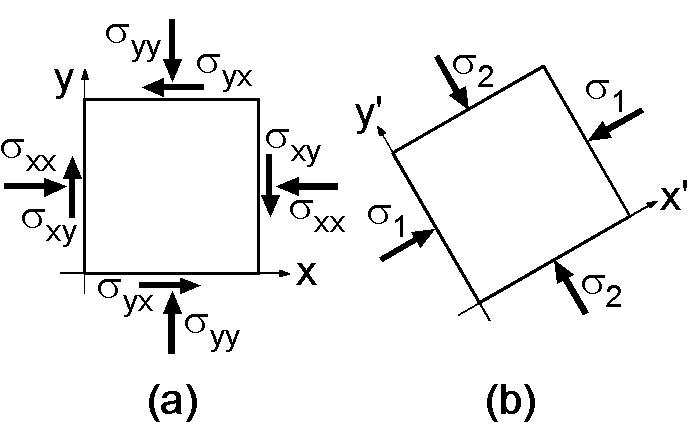
主応力軸と主応力： 図（a）は弾性体の中に任意に取った座標系での，ある微小体積部分に作用する応力の様子です．この座標系をある適当な角度回転すると，各座標軸に垂直な面ではずれ応力がゼロとなるような座標系が存在することが証明されています．即ち， \[ \sigma_{x'y'} = \sigma_{x'z'} = \sigma_{y'z'} = 0, \] となるような座標軸を主応力軸といいます．このときの各応力は主応力とよばれ， \(\sigma_1\)， \(\sigma_2\)， \(\sigma_3\) で表します（図（b））．対応する伸縮歪みは主歪みといい， \(\epsilon_1\)， \(\epsilon_2\)， \(\epsilon_3\) で表します．主応力軸の座標系では式 (5) は次のように表せます． \begin{eqnarray} \sigma_1 & = & (\lambda+2\mu)\epsilon_1 + \lambda\epsilon_2 + \lambda\epsilon_3, \nonumber \\ \sigma_2 & = & \lambda\epsilon_1 + (\lambda+2\mu)\epsilon_2 + \lambda\epsilon_3, \label{eq06} \\ \sigma_3 & = & \lambda\epsilon_1 + \lambda\epsilon_2 + (\lambda+2\mu)\epsilon_3. \nonumber \\ \end{eqnarray} 地殻中では，主応力軸の１つが鉛直方向となることが多く，プレート運動などにより３つの主応力の大きさの違いがある程度顕著になると，断層が動いて岩石破壊が生じます．３つの主応力が等しい場合は， \begin{equation} p = \sigma_1 = \sigma_2 = \sigma_3, \label{eq07} \end{equation} が圧力であり，静水圧と同じ状態になります．このように地中の応力分布が静水圧と同じ状態をリソスタティックな状態といい，この状態では岩石の破壊は発生しません．リソスタティックでない場合は，圧力は次のように３つの主応力の平均として定義されます． \begin{equation} p = \frac{1}{3}(\sigma_1 + \sigma_2 + \sigma_3). \label{eq08} \end{equation} また，主歪みによる体積 \(V\) の変化は， \(\delta V\) は膨張が正に対して，歪みは縮小が正ですので， \[ \frac{V + \delta V}{V} = (1 - \epsilon_1)(1 - \epsilon_2)(1 - \epsilon_3), \] となります．これを近似して，縮小を正として定義される体積変化 \(\Delta\) は次式となります． \begin{equation} \Delta = -\frac{\delta V}{V} = \epsilon_1 + \epsilon_2 + \epsilon_3. \label{eq09} \end{equation} ここで，(6) の各式を足すことで， \begin{eqnarray} p & = & \frac{\sigma_1 + \sigma_2 + \sigma_3}{3} = \frac{3\lambda+2\mu}{3}(\epsilon_1 + \epsilon_2 + \epsilon_3) = \frac{3\lambda+2\mu}{3}\Delta, \nonumber \\ & = & K\Delta. \end{eqnarray} ここに， \(K=(3\lambda+2\mu)/3\) は，体積弾性率（非圧縮率）で「→ ４-２ 地震波の伝播」でも扱いました．
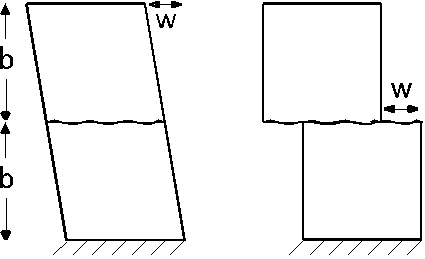
断層帯の地殻歪み： 地殻中でずれ応力が高まり，断層面におけるずれ歪みが岩石の限界値を超えると断層が動いて地震が発生します．図は横ずれ断層を上空から見た模式図で，図の左と右はそれぞれ地震発生の直前と直後の様子です． \(w\) を断層のずれ， \(b\) を断層帯片側の幅とすると，地震発生直前の地殻のずれ歪み \(\epsilon\) は式 (3) より， \[ \epsilon = (1/2)(w/2b) = w/4b, \] で求まります．仮に \(w\) = 4 m， \(b\) = 10 km とすると, \[ \epsilon = 4/(4\times 10\times 10^3) = 1\times 10^{-4}, \] となります．この歪みの原因となったずれ応力 \(\tau\) は，岩石の剛性率 \(\mu\) を 20 GPa とすると，式 (4) より， \[ \tau = 2\times20\times10^9\times1\times10^{-4} = 4\times10^6. \] すなわち， \(\tau\) = 4 MPa となります．この値は大気圧の約 0.1 MPa と比較して特に大きくないですが，実際には１ケタ以上大きいと考えられます．それは，地殻の中では断層面に垂直に働く圧縮応力のため，断層面の摩擦応力が増加して断層が滑りにくくなり，単純に式 (4) を適用できないためです．なお，ずれ応力は面や向きの添字を省略する場合は \(\sigma\) ではなく \(\tau\) で表わすのが一般的です．
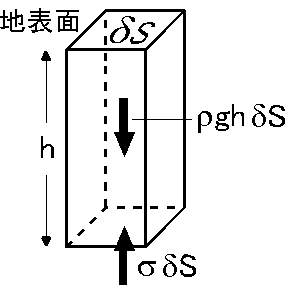
地殻内の応力： 地殻の中では岩石層自身の重さのため常に大きな圧縮応力が働いています．図のように，断面積 \(\delta S\)，高さ \(h\) の柱を考え，岩石の密度 \(\rho\) と重力加速度 \(g\) は一定とします．すると，底の面では柱の重さによる力 \(\rho gh\delta S\) と圧縮応力による力 \(\sigma\delta S\) がつりあい， \[ \sigma = \rho gh, \] の応力が働きます．この応力の大きさは， \(\rho\) = 2700 kg/m3， \(g\) = 10 m/s2 とすると，深さ 10 km では， \[ \sigma = 2700\times 10\times 10\times 10^3 = 270\times 10^6. \] 即ち， 270 MPa の大きな値となります．地殻の中では，岩石層の重さに起因した圧縮応力は地質学的時間スケールではあらゆる方向に働き，水中の圧力と似た状態になると考えられています．前述の通り，この状態を静水圧（hydrostatic）に習って，静岩石圧（lithostatic）の状態にあると表現します．結局，リソスタティックの状態での地殻の圧力 \(p\) は圧縮応力 \(\sigma\) に等しくなります． \begin{equation} p = \sigma = \rho gh. \label{eq11} \end{equation} このようなリソスタティックな状態では岩石破壊は生じず，断層が動くのはプレート運動などの原因で，３つの主応力の大きさの差がある限界値を超えた場合です．
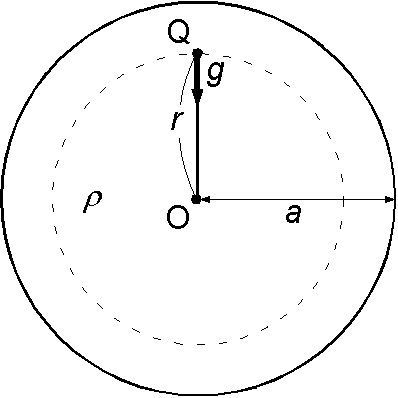
小天体内部の圧力： 上記のリソスタティックな状態にある地殻内部の圧力は，岩石の密度も重力加速度も一定と仮定して導きました．しかし，天体内部の圧力を求める際には密度も重力加速度も中心からの距離の関数となり大変難解な問題となります．そこで，密度は一定で重力加速度だけが変化するとして考えることにします．この密度一定のモデルは，月のような小天体には応用可能と思われます．
図のような密度 \(\rho\) で半径 \(a\) の天体を考え，内部の点 Q の中心からの距離 \(r\) を外向きを正とします．点 Q における圧力 \(p\) の， \(r\) が \(dr\) 増加したときの減少 \(dp\) は，重力加速度を \(g(r)\) として式 (11) より， \begin{equation} dp = -\rho g(r) dr, \label{eq12} \end{equation} と表せます．一方，点 Q における重力加速度は，点 Q より内側の部分の質量 \(M(r)\) だけによりますので（「３-５ 重力ポテンシャルとジオイド」の「→ 問題３-５-２ 解説」を参照）， \begin{equation} g(r) = \frac{GM(r)}{r^2} = \frac{4\pi \rho G}{3} r, \label{eq13} \end{equation} となります．但し， \(g(r)\) は内向きを正とし， \(G\) は万有引力定数です．式 (13) を用いて式 (12) を積分すると， \(C\) を積分定数として， \[ p = -\frac{2\pi\rho^2 G}{3}r^2 + C, \] となりますが， \(r=a\) で \(p=0\) として \(C\) を決めれば， \(p\) は次式となります． \begin{equation} p = \frac{2\pi\rho^2 G}{3}(a^2 - r^2). \label{eq14} \end{equation} この式から月の中心の圧力を， \(\rho\) = 3300 kg/m3， \(a\) = 1737 km として計算すると， \begin{eqnarray*} p & = & 2\times 3.14\times 3300^2\times 6.674\times 10^{−11}\times (1.737\times 10^6)^2\div 3, \\ & = & 4.59\times 10^9. \end{eqnarray*} 約 4.6 GPa となりました．
応力の単位： 応力（圧力）の単位はパスカル（Pa = N/m2）ですが，重量キログラム毎平方センチメートル（kgf/cm2），気圧（atm），バール（bar）もよく使われますので，これらの単位間の関係をまとめます．
- 1 kgf/cm2 = 9.80665 N/cm2 = 9.80665÷10-4 N/m2 = 9.80665×104 Pa,
- \(\qquad\quad\approx\) 0.1 MPa.
- 1 atm = 76×13.5951×10-3 kgf/cm2 = 76×13.5951×10-3×9.80665÷10-4 N/m2,
- \(\qquad\)= 1.01325×105 Pa = 1013.25 hPa,
- \(\qquad\)\(\approx\) 0.1 MPa.
- 1 bar = 106 dyn/cm2 = 106×10-5÷10-4 N/m2 = 105 Pa,
- \(\qquad\)= 0.1 MPa.
問題４-４-１
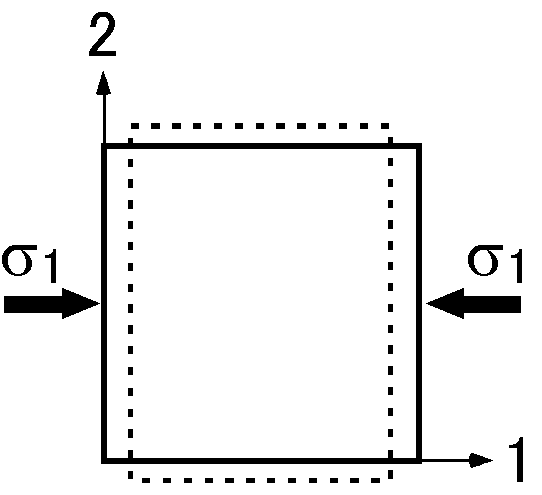
図は弾性体に圧縮応力 \(\sigma_1\) が働くと，その方向に縮むだけでなく，直角な２つの方向については伸びる様子を示します．この場合，主応力についての一般化されたフックの法則は，本文の式 (6) で \(\sigma_2=\sigma_3=0\) とおいて， \begin{eqnarray*} \sigma_1 & = & (\lambda+2\mu)\epsilon_1 + \lambda\epsilon_2 + \lambda\epsilon_3, \\ 0 & = & \lambda\epsilon_1 + (\lambda+2\mu)\epsilon_2 + \lambda\epsilon_3, \\ 0 & = & \lambda\epsilon_1 + \lambda\epsilon_2 + (\lambda+2\mu)\epsilon_3, \end{eqnarray*} となります．これらの式を解くことで次の関係式を導きなさい． \begin{eqnarray*} \epsilon_1 & = & \frac{\lambda + \mu}{\mu(3\lambda + 2\mu)}\sigma_1, \\ \epsilon_2 & = & \epsilon_3 = -\frac{\lambda}{2(\lambda + \mu)}\epsilon_1. \end{eqnarray*}
問題４-４-２
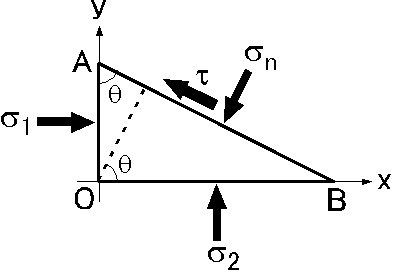
断層は理論上は最大圧縮応力軸と最小圧縮応力軸に対し 45° の傾きを持つことを２次元モデルで考えます．図のように \(x\) 軸と \(y\) 軸が主応力軸で， \(\sigma_1\) ≥ \(\sigma_2\) ≥ 0 とします．ある面 AB の法線方向が \(x\) 軸と \(\theta\) の角度をなすとき，その面に働く法線応力 \(\sigma_n\) とずれ応力 \(\tau\) が次式で表されることを，三角形 OAB に働く力のつり合いから導きなさい． \begin{eqnarray*} \sigma_n & = & \frac{1}{2}(\sigma_1 + \sigma_2) + \frac{1}{2}(\sigma_1 - \sigma_2)\cos 2\theta, \\ \tau & = & \frac{1}{2}(\sigma_1 - \sigma_2)\sin 2\theta. \end{eqnarray*} この結果から，断層が破壊して地震が発生するときの条件や断層の向きについて考察しなさい．
問題４-４-３
マントルと核による２層構造のリソスタティックな状態にある天体内部の圧力を考えます．天体の半径は \(a\)，核の半径は \(b\)，マントルの厚さは \(a-b\) です．核の密度 \(\rho_c\) とマントルの密度 \(\rho_m\) は深さによらず一定とします．
- （１） 内部の点 Q の中心からの距離 \(r\) は外向きを正，その点における重力加速度 \(g(r)\) は内向きを正とするとき，重力加速度 \(g(r)\) と圧力 \(p(r)\) は以下の式で与えられることを導きなさい． \begin{eqnarray*} g(r) & = & \frac{4}{3}\pi G\rho_c r \quad 0\leq r\leq b, \\ & = & \frac{4}{3}\pi G\left(\rho_m r+\frac{(\rho_c-\rho_m)b^3}{r^2}\right) \quad b\leq r\leq a. \end{eqnarray*} \begin{eqnarray*} p(r) & = & \frac{2}{3}\pi G\rho_m^2(a^2-r^2)+\frac{4}{3}\pi G\rho_m(\rho_c-\rho_m)b^3\left(\frac{1}{r}-\frac{1}{a}\right) \quad b\leq r\leq a, \\ & = & \frac{2}{3}\pi G\rho_c^2(b^2-r^2)+\frac{2}{3}\pi G\rho_m^2(a^2-b^2)+\frac{4}{3}\pi G\rho_m(\rho_c-\rho_m)b^3\left(\frac{1}{b}-\frac{1}{a}\right) \\ & \quad & 0\leq r\leq b. \end{eqnarray*}
- （２） このモデルを地球に適用し， \(a\) = 6371 km， \(b\) = 3480 km， \(\rho_m\) = 4400 kg/m3， \(\rho_c\) = 11200 kg/m3， \(G\) = 6.674×10-11 m3 kg-1 s-2 として，核-マントル境界と地球表面での重力加速度，及び，核-マントル境界と地球中心での圧力を計算しなさい．
参考文献：
- Turcotte, D. & G. Schubert, Geodynamics (Second Edition), 456 pp., Cambridge University Press, 2002.