3-5 重力ポテンシャルとジオイド
ベクトル場とポテンシャル: 一般に,位置の関数で表される物理量を場(ば)といいます.特に,ベクトル \({\bf f}\) が位置の関数で表されるときは \({\bf f}\) をベクトル場といい,万有引力,電場,磁場などが考えられます.また,ベクトル場 \({\bf f}\) が位置の関数であるスカラー \(V\) の空間微分 \begin{equation} {\bf f} = -\nabla V, \label{eq01} \end{equation} で表されるとき, \(V\) を \({\bf f}\) のポテンシャルといいます.ここに, \(\nabla\) (ナブラ) は次の微分演算子です. \begin{equation} \nabla = \left(\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}\right). \label{eq02} \end{equation}
ポテンシャル \(V\) の値が一定となるような面を等ポテンシャル面といいます.ベクトル場 \({\bf f}\) は等ポテンシャル面に常に垂直となりますが,これは次のようにして分かります.いま,ある点のポテンシャル \(V({\bf r})\) と微小距離 \(d{\bf r}\) 離れた点のポテンシャル \(V({\bf r}+d{\bf r})\) が等しいとします.即ち, \[ dV = V({\bf r}+d{\bf r}) - V({\bf r}) = 0. \] 全微分の公式より, \begin{eqnarray*} dV & = & \frac{\partial V}{\partial x}dx + \frac{\partial V}{\partial y}dy + \frac{\partial V}{\partial z}dz, \\ & = & \left(\frac{\partial V}{\partial x},\frac{\partial V}{\partial y},\frac{\partial V}{\partial z}\right)\cdot (dx,dy,dz), \\ & = & -{\bf f}\cdot d{\bf r} = 0. \end{eqnarray*} よって, \({\bf f}\) と \(d{\bf r}\) は直交し,ベクトル場 \({\bf f}\) は等ポテンシャル面に垂直となります.
ベクトル場 \({\bf f}\) をある経路に沿って積分すると,その結果は経路に依存しないことが分かります. \begin{eqnarray} \int_{\bf r_0}^{\bf r_1}{\bf f}\cdot d{\bf r} & = & \int_{\bf r_0}^{\bf r_1} -\nabla V\cdot d{\bf r}, \nonumber \\ & = & -\int_{\bf r_0}^{\bf r_1} \frac{\partial V}{\partial x}dx + \frac{\partial V}{\partial y}dy + \frac{\partial V}{\partial z}dz, \nonumber \\ & = & -\int_{\bf r_0}^{\bf r_1} dV, \nonumber \\ & = & -V({\bf r_1}) + V({\bf r_0}). \label{eq03} \end{eqnarray} 式 (3) の左辺は \({\bf f}\) を力とすれば,力がした仕事です.よって, (3) はその仕事が経路に関わらず最初と最後のポテンシャルの差だけで決まることを示します.そのため,ポテンシャルはポテンシャルエネルギーとも言われます.また,このようなベクトル場は保存ベクトル場と言われます.
重力ポテンシャル: 重力によるポテンシャルを重力ポテンシャルといいます.測地学の専門レベルでは重力加速度を重力と表現します.ここでも重力ポテンシャルを単位質量の物体の位置エネルギーと考えます.よって,重力ポテンシャルの空間微分は重力加速度になります.また,測地学では (1) の空間微分の式に負記号を付けませんが,ここでは基礎レベルの物理学に従い式 (1) を使用します.
地表付近の重力ポテンシャルについて考えると,重力加速度は一定の \(g\) で鉛直下向きですので,1次元の問題となります.そこで, \(z\) 軸を地表から上向きに取ると,質量 \(m\) の質点の位置エネルギーは \(mgz\) です(→ 1-3 エネルギー保存則と運動量保存則).よって,この場合の重力ポテンシャル \(V\) と重力加速度ベクトル \({\bf g}\) の \(z\) 成分 \(g_z\) は次のようになります. \[ V = gz, \quad g_z = -\frac{dV}{dz} = -g. \]
地球規模の重力加速度については,地球の中心を原点とし,考えている地点の鉛直上向きに \(r\) 軸を取れば1次元として扱えます.万有引力定数を \(G\),地球の質量を \(M\) として,重力ポテンシャル \(V\) と重力加速度 \({\bf g}\) の \(r\) 成分 \(g_r\) は次のようになります. \[ V = -\frac{GM}{r}, \quad g_r = -\frac{dV}{dr} = -\frac{d}{dr}\left(-\frac{GM}{r}\right) = -\frac{GM}{r^2}. \]
一方,遠心力にもポテンシャルがあります.単位質量の質点が半径 \(\ell\) の円軌道を角速度 \(\omega\) で回転しているときの遠心力は外向きに \(\ell\omega^2\) ですので,遠心力によるポテンシャルと遠心力による加速度ベクトル \({\bf a}\) の外向き成分 \(a\) は次式で表されます. \[ V = -\frac{1}{2}\ell^2\omega^2, \quad a = -\frac{dV}{d\ell} = \ell\omega^2. \] そこで,地球の重力は引力と自転の遠心力の合力ですので,重力ポテンシャルはそれらのポテンシャルの和で表せます.経度方向に力は働かないので,2次元の球座標 \(r,\theta\) で考えると,重力ポテンシャルは次式で表せます.但し, \(r\) は地球中心からの距離, \(\theta\) は余緯度で子午面内で北極からの角度です. \begin{equation} V = -\frac{GM}{r} - \frac{1}{2}r^2\omega^2\sin^2\theta. \label{eq04} \end{equation} 球座標では, \(\nabla = \left(\frac{\partial}{\partial r}, \frac{1}{r}\frac{\partial}{\partial\theta}\right)\) ですので,重力加速度の \(r\) 成分と \(\theta\) 成分は, \begin{eqnarray} g_r & = & -\frac{\partial V}{\partial r} = -\frac{GM}{r^2} + r\omega^2\sin^2\theta, \label{eq05} \\ g_\theta & = & -\frac{1}{r}\frac{\partial V}{\partial\theta} = r\omega^2\sin\theta\cos\theta. \label{eq06} \end{eqnarray} ここで注意すべき点は,(6) によると重力加速度 \({\bf g}\) は子午線に沿った南向きの成分を含むことです.そのため,例えば海水は赤道の方へ流れてしまい,海洋は赤道で深く極で浅いことになります.実際の地球がこれと異なるのは地球の形が球ではなく,回転楕円体に近いからです.
ジオイド: 地球の形を球とすると, (5) と (6) により重力加速度は地表に垂直ではなく,地表は水平面ではありません.これは自転する球の表面は等ポテンシャル面ではないためです.重力理論によると,回転楕円体をその扁平率,密度,慣性モーメントなどを地球に適合するよう定めることで,その表面を等ポテンシャル面とすることができます.このようにして地球の形と重力ポテンシャルを近似するよう定めた回転楕円体を地球楕円体といいます.
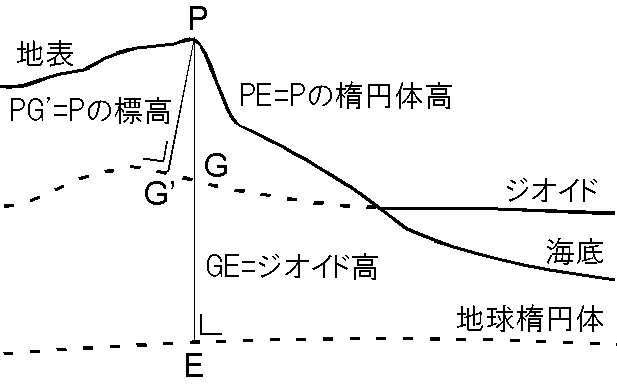
一方,海上では平均海水面は水平面であり,重力は海面に垂直ですので,等ポテンシャル面となります.そこで,平均海水面,及び陸上では仮想的な海面をジオイドといい,標高の基準としました.ある地点の標高を海抜で表現するのはそのためです.ジオイドは地球楕円体とは通常 30〜50 m 程度ずれがあり,図にジオイド,地球楕円体,標高などの関係を示します. P 点の標高とは P からジオイドへ下ろした垂線の距離 PG' で,地球楕円体へ下ろした垂線の距離 PE の楕円体高とは異なります.また,距離 GE をジオイド高といいます.標高は水準測量で決定し,楕円体高は衛星測位から決定します. GPS 機器で標高が正しく求まるのは,各地のジオイド高の情報が入力されているためです.但し,図から PG' と PE は僅かですが傾きの偏差があり (鉛直線偏差または垂直線偏差),高精度の測量ではその情報も必要になるようです.
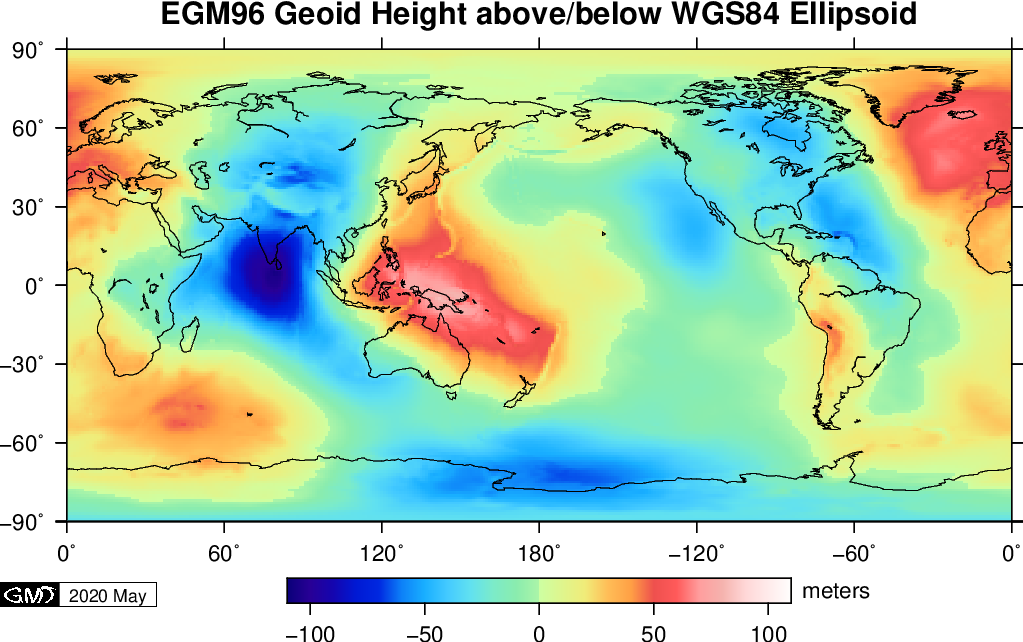
ジオイドは地球の表面の地形や内部の密度の不均質などの原因で最大で 100 m 程度の起伏があり,下図に世界のジオイド高の分布を示します.起伏の多くについて,プレートテクトニクスやマントル対流との関係が指摘されているようです.しかし, -100 m 以上にもなる最も深い窪みであるインドの南の領域については原因は不明のようです.ここで注意すべき点は,この領域を船が航行すると実際に 100 m 降下し再び 100 m 上昇しますが,その間には重力エネルギーの出入りはないことです.また,降りる途中で船が停止しても船が落ちて行くことはないです.ジオイドはたとえ起伏があっても等ポテンシャル面,即ち水平面だからです.なお,等ポテンシャル面では重力の大きさは必ずしも等しくないことも注意が必要です.
問題3-5-1
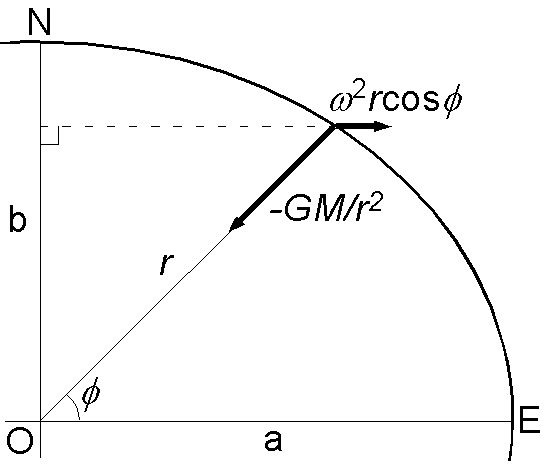
17 世紀にホイヘンスは地球の全質量がその中心に集中していると仮定し,地球の扁平率として 1/578 を得ました.これを重力ポテンシャルから求めます.
図のように,地球を密度一様で質量が \(M\) の回転楕円体とし,角速度 \(\omega\) で自転しているとします.地球の全質量が回転楕円体の中心に集中しているとすると,引力と遠心力の合力による重力ポテンシャル \(V\) は地球中心からの距離 \(r\),緯度 \(\phi\) の地点で次式で表せます. \[ V = -\frac{GM}{r} - \frac{1}{2}r^2\omega^2\cos^2\phi. \]
(1) 重力ポテンシャルが極 N と赤道 E で等しいとして,扁平率が次式で与えられることを導きなさい. \[ f = 1 - \frac{b}{a} = \frac{3\omega^2}{8\pi G\rho}. \] 但し, \(G\) は万有引力定数, \(\rho\) は回転楕円体の密度です.なお,回転楕円体の体積は \(4\pi a^2b/3\) です.
(2) 次の定数の値を用いて地球の扁平率を求めなさい. \begin{eqnarray*} G & = & 6.674\times 10^{-11}\ \mathrm{m^3\,kg^{-1}\,s^{-2}},\\ \omega & = & 2\pi\div(0.9973\times 24\times 3600) = 7.292\times 10^{-5}\ \mathrm{s^{-1}},\\ \rho & = & 5500\ \mathrm{kg/m^3}. \end{eqnarray*}
【補足】 全質量が中心に集中しているとする仮定は,次の問題3-5-2のように球では成立しますが回転楕円体には適用できません.より高い近似による方法は → このページで解説しています.
問題3-5-2
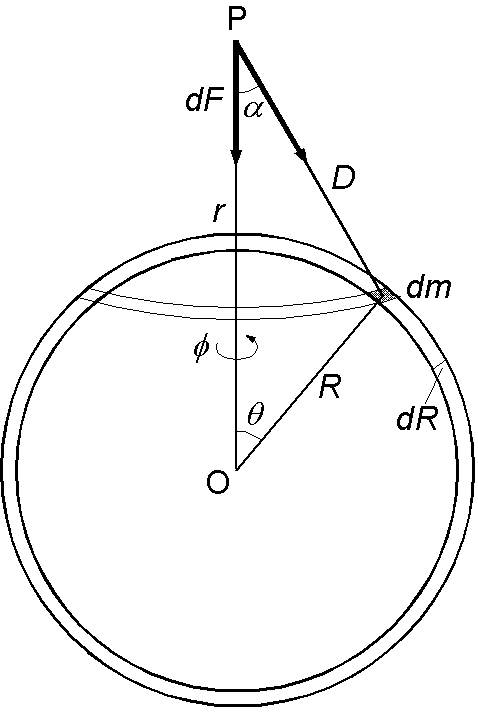
球による引力は球の中心に全質量が集中した質点による引力と同等です.これを図のように,球の内部の微小部分の質量 \(dm\) が中心から距離 \(r\) の点 P に位置する質点に及ぼす力を球全体で積分することで導きます.但し,点 P は球の外部で,質点は単位質量とします.(より簡単なポテンシャルによる方法は次問題で扱います)
\(dm\) による力を PO 方向の成分 \(dF\) と直交する成分に分けると,後者は PO の回りの対称性から積分するとゼロですので,前者のみを考えます.万有引力定数を \(G\),球の密度を \(\rho\) とし,各変数を図のように取り, \(dm\) の体積 \(dR\times Rd\theta\times R\sin\theta d\phi\) を考慮して, \begin{eqnarray*} dF & = & \frac{G}{D^2}\cos\alpha dm, \\ & = & \frac{G}{D^2}\cos\alpha \rho R^2\sin\theta dR d\theta d\phi. \end{eqnarray*} これを球の半径を \(a\) として積分し,球の質量を \(M\) として \(F\) を与える式を導きなさい.但し,次の関係式を利用し,途中で \(\theta\) の積分は \(D\) による積分に変換します. \begin{eqnarray*} \cos\alpha & = & \frac{D^2 + r^2 - R^2}{2rD}, \\ D & = & \sqrt{r^2 + R^2 - 2rR\cos\theta}, \\ dD & = & \frac{rR\sin\theta}{\sqrt{r^2 + R^2 - 2rR\cos\theta}}d\theta = rR\frac{\sin\theta}{D}d\theta. \end{eqnarray*}
問題3-5-3
前問と同じ球による引力をポテンシャルから導きます.微小部分の質量 \(dm\) による点 P のポテンシャル \(dV\) を球全体で積分し球によるポテンシャル \(V\) を求めます. \[ dV = -\frac{G}{D}dm = -\frac{G}{D}\rho R^2\sin\theta dR d\theta d\phi. \] 積分では, \(D=\sqrt{r^2+R^2-2rR\cos\theta}\) を微分して得られる, \[ \frac{1}{rR}dD = \frac{\sin\theta}{D}d\theta, \] を用いて積分変数を \(\theta\) から \(D\) へ変換します.
球の半径を \(a\),質量を \(M\) として,点 P における球の引力による加速度 \(g\) (単位質量の質点が受ける力) を求めなさい.