問題4−4−1 解答
kgf/cm2, atm, bar を Pa で表す変換式は以下の通りです. \begin{eqnarray*} 1\ \mathrm{kgf/cm^2} & = & 9.80665\ \mathrm{N/cm^2} = 9.80665\div 10^{-4}\ \mathrm{N/m^2} = 9.80665\times 10^4\ \mathrm{Pa} \approx 0.1\ \mathrm{MPa}. \\ 1\ \mathrm{atm} & = & 76\times 13.5951\times 10^{-3}\ \mathrm{kgf/cm^2} \\ & = & 76\times 13.5951\times 10^{-3}\times 9.80665\div 10^{-4}\ \mathrm{N/m^2} \\ & = & 1.01325\times 10^5\ \mathrm{Pa} = 1013.25\ \mathrm{hPa} \approx 0.1\ \mathrm{MPa}. \\ 1\ \mathrm{bar} & = & 10^6\ \mathrm{dyn/cm^2} = 10^6\times 10^{-5}\div 10^{-4}\ \mathrm{N/m^2} = 10^5\ \mathrm{Pa} = 0.1\ \mathrm{MPa}. \end{eqnarray*}
問題4−4−2 解答
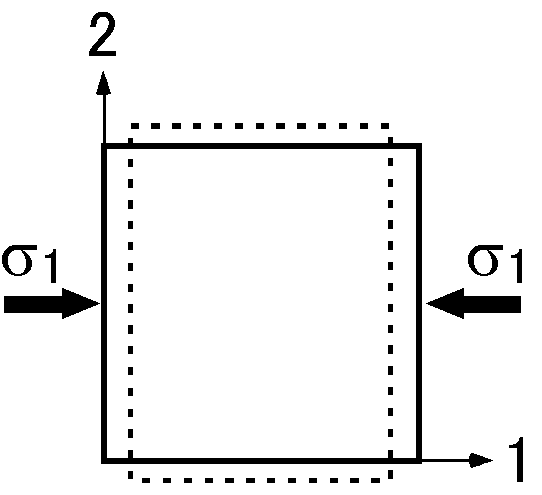
本文の式 (6) で \(\sigma_2\) = \(\sigma_3\) = 0 とおくと次のようになります. \begin{eqnarray} \sigma_1 & = & (\lambda+2\mu)\epsilon_1 + \lambda\epsilon_2 + \lambda\epsilon_3, \label{eq01} \\ 0 & = & \lambda\epsilon_1 + (\lambda+2\mu)\epsilon_2 + \lambda\epsilon_3, \label{eq02} \\ 0 & = & \lambda\epsilon_1 + \lambda\epsilon_2 + (\lambda+2\mu)\epsilon_3. \label{eq03} \end{eqnarray} 式 (2) から式 (3) を引くと, \[ 2\mu\epsilon_2 - 2\mu\epsilon_3 = 0, \] より, \[ \epsilon_2 = \epsilon_3. \] これを式 (2) または (3) に代入して, \begin{equation} \epsilon_2 = \epsilon_3 = -\frac{\lambda}{2(\lambda + \mu)}\epsilon_1. \label{eq04} \end{equation} この結果を式 (1) に代入すると, \begin{eqnarray} \sigma_1 & = & (\lambda + 2\mu)\epsilon_1 - \frac{\lambda^2}{\lambda + \mu}\epsilon_1, \nonumber \\ & = & \frac{\mu(3\lambda + 2\mu)}{\lambda + \mu}\epsilon_1. \label{eq05} \end{eqnarray} \(\epsilon_1\) で表わして, \begin{equation} \epsilon_1 = \frac{\lambda + \mu}{\mu(3\lambda + 2\mu)}\sigma_1. \label{eq06} \end{equation}
問題4−4−3 解答
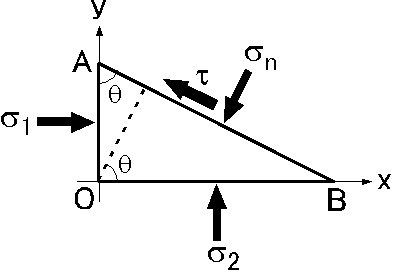
力のつり合いの式は \(x\) 軸方向と \(y\) 軸方向のそれぞれについて, \begin{eqnarray} \sigma_1 \mathsf{\overline{OA}} & = & \tau \mathsf{\overline{AB}}\sin\theta + \sigma_n \mathsf{\overline{AB}}\cos\theta, \label{eq07} \\ \sigma_2 \mathsf{\overline{OB}} & = & -\tau \mathsf{\overline{AB}}\cos\theta + \sigma_n \mathsf{\overline{AB}}\sin\theta. \label{eq08} \end{eqnarray} 但し, \(\mathsf{\overline{OA}}\), \(\mathsf{\overline{OB}}\), \(\mathsf{\overline{AB}}\) はそれぞれ線分 OA, OB, AB の長さですが,ここでは面積に相当します.式 (7) と式 (8) の両辺を \(\mathsf{\overline{AB}}\) で除して, \[ \frac{\mathsf{\overline{OA}}}{\mathsf{\overline{AB}}} = \cos\theta, \quad \frac{\mathsf{\overline{OB}}}{\mathsf{\overline{AB}}} = \sin\theta, \] を代入すると, \begin{eqnarray} \sigma_1\cos\theta & = & \tau\sin\theta + \sigma_n\cos\theta, \label{eq09} \\ \sigma_2\sin\theta & = & -\tau\cos\theta + \sigma_n\sin\theta. \label{eq10} \end{eqnarray} (9)×\(\cos\theta\) + (10)×\(\sin\theta\),及び (9)×\(\sin\theta\) - (10)×\(\cos\theta\) より, \begin{eqnarray} \sigma_n & = & \sigma_1\cos^2\theta + \sigma_2\sin^2\theta, \label{eq11} \\ \tau & = & (\sigma_1 - \sigma_2)\sin\theta\cos\theta. \label{eq12} \end{eqnarray} さらに, \[ \cos^2\theta=\frac{1+\cos 2\theta}{2},\quad \sin^2\theta=\frac{1-\cos 2\theta}{2},\quad \sin\theta\cos\theta=\frac{1}{2}\sin 2\theta, \] を用いて, \begin{eqnarray} \sigma_n & = & \frac{1}{2}(\sigma_1 + \sigma_2) + \frac{1}{2}(\sigma_1 - \sigma_2)\cos 2\theta, \label{eq13} \\ \tau & = & \frac{1}{2}(\sigma_1 - \sigma_2)\sin 2\theta. \label{eq14} \end{eqnarray}
面 AB の破壊は AB に働くずれ応力 \(\tau\) がある限界値 \(\tau_c\) を超えると発生します.式 (14) によると, \(\tau\) は主応力の差 \(\sigma_1\) - \(\sigma_2\)(差応力)に比例し, \(\theta\) = 45° で最大となります.よって,断層の破壊は差応力 \(\sigma_1\) - \(\sigma_2\) が \(\tau_c\) の2倍を超えたときに発生し,断層面の向きは2つの主応力軸から 45° の方向です.
しかし,面 AB に破壊が生じる限界のずれ応力 \(\tau_c\) は,面 AB に働く法線応力 \(\sigma_n\) に比例して大きくなることが知られています.従って,必ずしも断層の破壊は \(\theta\) = 45° で発生するとは限りません.式 (13) によると, \(\sigma_n\) は \(\theta\) = 0° で最大値 \(\sigma_1\), \(\theta\) = 90° で最小値 \(\sigma_2\) となります.そのため, \(\theta\) が 45° 以下では,大きな \(\sigma_n\) のため \(\tau_c\) も大きく断層破壊は発生しませんが, 45° を超えると \(\tau\) は小さくなるものの,減少した \(\sigma_n\) のために \(\tau_c\) もさらに小さくなり,断層が破壊するということが考えられます.このような場合には,断層面の傾きは最大圧縮軸から 45° より小さい角度となります.
上の考察は既存の断層面が存在するときには成立しません.それは,過去に動いたことがある断層面は脆弱で,小さなずれ応力の発生でも破壊することがあるからです.