問題3-5-2 解説
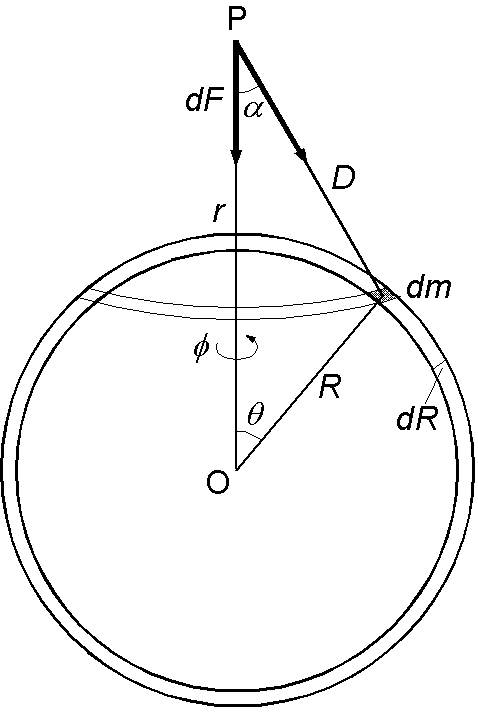
\(dF=\frac{G}{D^2}\cos\alpha dm\) を \(\phi\) は 0 から 2π, \(\theta\) は 0 から π, \(R\) は 0 から \(a\) まで積分します. \[ F = \int\int\int\frac{G}{D^2}\cos\alpha dm = \int_0^a dR\int_0^\pi d\theta\int_0^{2\pi}\frac{G}{D^2}\cos\alpha \rho R^2\sin\theta d\phi. \] \(\cos\alpha\) に余弦公式を適用して式を変形します. \begin{eqnarray*} F & = & 2\pi\rho G\int_0^a dR\int_0^\pi\frac{D^2+r^2-R^2}{2rD}\frac{1}{D^2}R^2\sin\theta d\theta, \\ & = & \frac{\pi\rho G}{r}\int_0^a dR\int_0^\pi\left(1+\frac{r^2-R^2}{D^2}\right)R^2\frac{\sin\theta}{D}d\theta. \end{eqnarray*} ここで, \(D=\sqrt{r^2 + R^2 - 2rR\cos\theta}\) を \(\theta\) で微分すると, \[ dD = \frac{rR\sin\theta}{\sqrt{r^2 + R^2 - 2rR\cos\theta}}d\theta = rR\frac{\sin\theta}{D}d\theta, \] 即ち, \[ \frac{\sin\theta}{D}d\theta = \frac{1}{rR}dD, \] の関係を使用して,積分変数を \(\theta\) から \(D\) へ変換します. \begin{eqnarray*} F & = & \frac{\pi\rho G}{r^2}\int_0^a dR\int_{r-R}^{r+R}\left(1+\frac{r^2-R^2}{D^2}\right)R dD, \\ & = & \frac{\pi\rho G}{r^2}\int_0^a dR\left[D - \frac{r^2-R^2}{D}\right]_{r-R}^{r+R} R, \\ & = & \frac{\pi\rho G}{r^2}\int_0^a dR\left(r+R-r+R-\frac{r^2-R^2}{r+R}+\frac{r^2-R^2}{r-R}\right)R, \\ & = & \frac{\pi\rho G}{r^2}\int_0^a R(r+R-r+R-r+R+r+R)dR, \\ & = & \frac{4\pi\rho G}{r^2}\int_0^a R^2 dR = \frac{4\pi\rho G}{r^2}\frac{a^3}{3} = \frac{GM}{r^2}. \end{eqnarray*}
補足:球殻の内部の点には力が働かないことについて
上図で,点 P が厚さ \(dR\) の球殻の内部(球殻で囲まれた空間)にある場合, P より上部の球殻による力と下部の球殻による力が相殺して,点 P には力が働かないことが予想されます.この場合,三角形 P-dm-O の角 \(\alpha\) が鈍角から鋭角まで変化しますが,上で導いた積分の式はそのまま使えます.但し, \(D\) の積分範囲が \(R-r\) から \(R+r\) となります.よって,半径 \(R\),厚さ \(dR\) の球殻の全質量による力 \(dF\) は, \begin{eqnarray*} dF & = & \frac{\pi\rho G}{r^2}\int_{R-r}^{R+r}\left(1+\frac{r^2-R^2}{D^2}\right)R dD, \\ & = & \frac{\pi\rho GR}{r^2}\left[D - \frac{r^2-R^2}{D}\right]_{R-r}^{R+r}, \\ & = & \frac{\pi\rho GR}{r^2}\left(R+r-R+r-\frac{r^2-R^2}{R+r}+\frac{r^2-R^2}{R-r}\right), \\ & = & \frac{\pi\rho GR}{r^2}(R+r-R+r+R-r-R-r) = 0. \end{eqnarray*}
この結果から,球の内部で半径 \(r\) に位置する質点に働く力は,その点より内側の部分の質量だけから力を受けることが分かります.球の密度を \(\rho\),質点は単位質量とすれば力は, \[ F = G\rho\frac{4\pi r^3}{3}\frac{1}{r^2} = \frac{4\pi\rho G}{3}r, \] となります.例えば,地球内部の重力は地球中心からの距離に比例し,中心でゼロになります.