問題1−2−1 解答
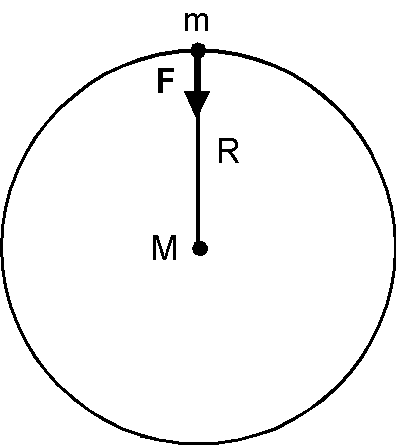
地球を密度が一様な球とすると,地球による引力は地球中心の質量 \(M\) の質点による引力と見なせるので,万有引力の法則より, \[ F = G\frac{Mm}{R^2}. \] 一方,運動方程式より物体は力 \(F\) により加速度を得ますが,慣習上これを重力加速度 \(g\) と記すと, \[ F = mg. \] 両式を等しいと置くと, \(m\) は消去され, \[ g = \frac{GM}{R^2}, \] となり,重力加速度は物体の質量には依存しないことが分かります.
問題1−2−2 解答
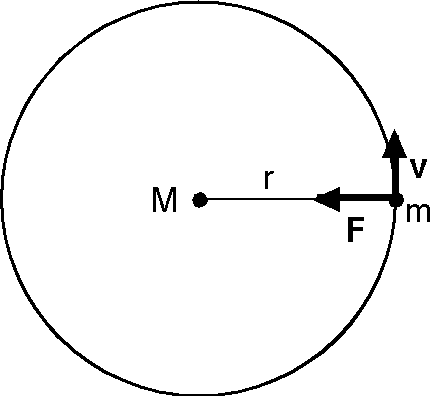
図のように,質量 \(M\) の太陽と質量 \(m\) の惑星の間には万有引力 \(F\) が働きますが,この力が速度 \(v\) で等速円運動する惑星に働く向心力となっています. \[ F = G\frac{Mm}{r^2} = mr\omega^2. \] よって, \[ \frac{1}{r^3\omega^2} = \frac{1}{GM}. \] 角速度 \(\omega\) を周期 \(T\) に置き換えて, \[ \frac{T^2}{r^3} = \frac{4\pi^2}{GM}. \] これは万有引力定数と太陽の質量だけで決まる一定値です.
問題1−2−3 解答
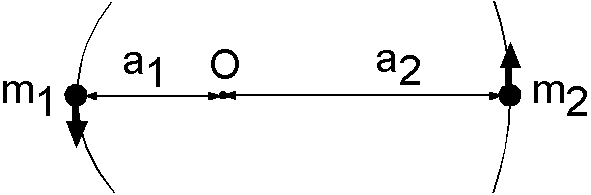
主星については,重心 O の回りの半径 \(a_1\) の円運動による向心力と,距離が \(a=a_1+a_2\) 離れた伴星との間に働く万有引力を等しいとおき, \[ m_1 a_1 \omega^2 = G\frac{m_1 m_2}{a^2}. \] この式から \(m_1\) を消去して整理すると, \[ a_1 a^2\omega^2 = G m_2. \] 伴星についても同様にして, \[ a_2 a^2\omega^2 = G m_1. \] これらの式を足し合わせて, \[ (a_1 + a_2)a^2\omega^2 = G(m_2 + m_1). \] これに, \(a=a_1+a_2\) と \(\omega = 2\pi/T\) を代入して整理すると,次の一般化されたケプラーの第3法則となります. \[ \frac{a^3}{T^2} = \frac{G}{4 \pi^2} (m_1 + m_2). \]