問題５−４−１ 解答

（１）　(a) 10 Ma については， \begin{eqnarray*} 2.02\sqrt{\kappa t} & = & 2.02\times\sqrt{(1\times 10^{-6})\times(10\times 10^6)\times(365\times 24\times 3600)} \\ & = & 3.59\times 10^4\ \mathrm{m}. \end{eqnarray*} となり，約 36 km です．同様に， (b) 50 Myr = 1.5768×10¹⁵ s と (c) 100 Myr = 3.1536×10¹⁵ s については，それぞれ 80.2 km と 113 km となります．

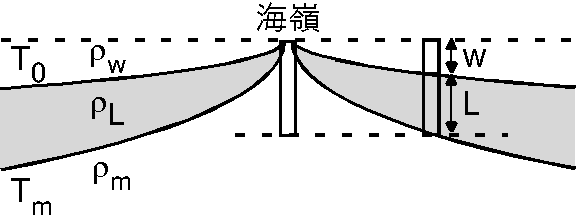
（２） 下の点線を補償面とし圧力の釣り合いより， \begin{eqnarray*} \rho_m(w + L) & = & \rho_w w + \rho_L L, \\ (\rho_m-\rho_w)w & = & (\rho_L - \rho_m)L, \\ w & = & \frac{\rho_L-\rho_m}{\rho_m-\rho_w}L. \end{eqnarray*}

（３） \(\alpha\) = 3.3×10^-5 1/K， \(T_m\) = 1300 °C， \(\rho_m\) = 3300 kg/m³ を用いて， \begin{eqnarray*} \rho_L - \rho_m & = & \frac{1}{2}\alpha T_m\rho_m, \\ & = & \frac{1}{2}\times (3.3\times 10^{-5})\times 1300\times 3300 = 70.785\ \mathrm{kg/m^3}. \end{eqnarray*} \(L\) = 100 km， \(\rho_w\) = 1000 kg/m³ より， \[ w = \frac{\rho_L-\rho_m}{\rho_m-\rho_w}L = \frac{70.785}{3300-1000}\times(100\times 10^3) = 3.08\times 10^3\ \mathrm{m}. \] 約 3.1 km となりましたが，海嶺の頂上は海面から 2~3 km ですので，海底の深さはおよそ 5~6 km となります．これは，およそ１億年で厚さ 100 km 程度となった海洋リソスフェアとして，よく観測される値です．ここで仮定したリソスフェアの温度構造は大変簡単ですが，実際の観測値とかなり合うことが分かります．

問題５−４−２ 解答

本文の式 (12)， \[ q_0 = -k\left[\frac{\partial T}{\partial z}\right]_{z=0} = -\frac{k(T_m-T_0)}{\sqrt{\pi\kappa t}}, \] より， \[ \left[\frac{\partial T}{\partial z}\right]_{z=0} = \frac{T_m-T_0}{\sqrt{\pi\kappa t}}. \] これを \(t\) について解いて， \[ t = \frac{(T_m-T_0)^2}{\pi\kappa[\partial T/\partial z]_{z=0}^2}. \] この式に， \([\partial T/\partial z]_{z=0}\) = 0.025 °C/m， \(T_m\) = 2000 °C， \(T_0\) = 0°C， \(\kappa\) = 1×10^-6 m²/s を代入すると， \begin{eqnarray*} t & = & \frac{2000^2}{3.14\times(1\times 10^{-6})\times(2.5\times 10^{-2})^2} = 2.0382\times 10^{15}\ \mathrm{s}, \\ & = & 6.4631\times 10^7\ \mathrm{yr} = 64.6\ \mathrm{Myr}. \end{eqnarray*} 地球の年齢は約 65 Myr（６千５百万年）という若い年齢となりました．

半無限体冷却モデルが地球の年齢に適用できない理由は本文に記したとおりですが，この簡単な１次元のモデルは海洋リソスフェアの冷却など，地球表層部を扱うプレートテクトニクスでは多くの事象を説明できます．

→ ホーム