誤差関数と相補誤差関数のグラフと数値表
誤差関数 \({\rm erf}(x)\) と相補誤差関数 \({\rm erfc}(x)\) は次のように定義されます. \begin{eqnarray*} {\rm erf}(x) & = & \frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}dt, \\ {\rm erfc}(x) & = & 1 - {\rm erf}(x) = \frac{2}{\sqrt{\pi}}\int_x^\infty e^{-t^2}dt. \end{eqnarray*} これらの関数は特殊関数である不完全ガンマ関数の特別な場合です.以下のグラフと数値表の作成には Press et al. (1992) による数値計算コードを使用しました.なお,分野によっては,上式の規格化係数 \(\frac{2}{\sqrt{\pi}}\) を付けない定義もありますので注意が必要です.
参考文献:
- Press, W.H., S.A. Teukolsky, W.T. Vetterling, and B.P. Flannery, Numerical Recipes in C: The Art of Scientific Computing (Second Edition), 994 pp., Cambridge University Press, Cambridge, 1992.
グラフ:
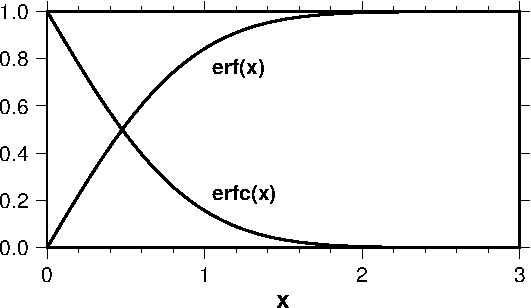
数値表:
| x | erf(x) | erfc(x) |
|---|---|---|
| 0.00 | 0.000000 | 1.000000 |
| 0.01 | 0.011283 | 0.988717 |
| 0.02 | 0.022565 | 0.977435 |
| 0.03 | 0.033841 | 0.966159 |
| 0.04 | 0.045111 | 0.954889 |
| 0.05 | 0.056372 | 0.943628 |
| 0.06 | 0.067622 | 0.932378 |
| 0.07 | 0.078858 | 0.921142 |
| 0.08 | 0.090078 | 0.909922 |
| 0.09 | 0.101281 | 0.898719 |
| 0.10 | 0.112463 | 0.887537 |
| 0.11 | 0.123623 | 0.876377 |
| 0.12 | 0.134758 | 0.865242 |
| 0.13 | 0.145867 | 0.854133 |
| 0.14 | 0.156947 | 0.843053 |
| 0.15 | 0.167996 | 0.832004 |
| 0.16 | 0.179012 | 0.820988 |
| 0.17 | 0.189992 | 0.810008 |
| 0.18 | 0.200936 | 0.799064 |
| 0.19 | 0.211840 | 0.788160 |
| 0.20 | 0.222703 | 0.777297 |
| 0.21 | 0.233522 | 0.766478 |
| 0.22 | 0.244296 | 0.755704 |
| 0.23 | 0.255023 | 0.744977 |
| 0.24 | 0.265700 | 0.734300 |
| 0.25 | 0.276326 | 0.723674 |
| 0.26 | 0.286900 | 0.713100 |
| 0.27 | 0.297418 | 0.702582 |
| 0.28 | 0.307880 | 0.692120 |
| 0.29 | 0.318283 | 0.681717 |
| 0.30 | 0.328627 | 0.671373 |
| 0.31 | 0.338908 | 0.661092 |
| 0.32 | 0.349126 | 0.650874 |
| 0.33 | 0.359279 | 0.640721 |
| 0.34 | 0.369365 | 0.630635 |
| 0.35 | 0.379382 | 0.620618 |
| 0.36 | 0.389330 | 0.610670 |
| 0.37 | 0.399206 | 0.600794 |
| 0.38 | 0.409009 | 0.590991 |
| 0.39 | 0.418739 | 0.581261 |
| 0.40 | 0.428392 | 0.571608 |
| 0.41 | 0.437969 | 0.562031 |
| 0.42 | 0.447468 | 0.552532 |
| 0.43 | 0.456887 | 0.543113 |
| 0.44 | 0.466225 | 0.533775 |
| 0.45 | 0.475482 | 0.524518 |
| 0.46 | 0.484655 | 0.515345 |
| 0.47 | 0.493745 | 0.506255 |
| 0.48 | 0.502750 | 0.497250 |
| 0.49 | 0.511668 | 0.488332 |
| 0.50 | 0.520500 | 0.479500 |
| 0.52 | 0.537899 | 0.462101 |
| 0.54 | 0.554939 | 0.445061 |
| 0.56 | 0.571616 | 0.428384 |
| 0.58 | 0.587923 | 0.412077 |
| 0.60 | 0.603856 | 0.396144 |
| 0.62 | 0.619411 | 0.380589 |
| 0.64 | 0.634586 | 0.365414 |
| 0.66 | 0.649377 | 0.350623 |
| 0.68 | 0.663782 | 0.336218 |
| 0.70 | 0.677801 | 0.322199 |
| 0.72 | 0.691433 | 0.308567 |
| 0.74 | 0.704678 | 0.295322 |
| 0.76 | 0.717537 | 0.282463 |
| 0.78 | 0.730010 | 0.269990 |
| 0.80 | 0.742101 | 0.257899 |
| 0.82 | 0.753811 | 0.246189 |
| 0.84 | 0.765143 | 0.234857 |
| 0.86 | 0.776100 | 0.223900 |
| 0.88 | 0.786687 | 0.213313 |
| 0.90 | 0.796908 | 0.203092 |
| 0.92 | 0.806768 | 0.193232 |
| 0.94 | 0.816271 | 0.183729 |
| 0.96 | 0.825424 | 0.174576 |
| 0.98 | 0.834231 | 0.165769 |
| 1.00 | 0.842701 | 0.157299 |
| 1.05 | 0.862436 | 0.137564 |
| 1.10 | 0.880205 | 0.119795 |
| 1.15 | 0.896124 | 0.103876 |
| 1.20 | 0.910314 | 0.089686 |
| 1.25 | 0.922900 | 0.077100 |
| 1.30 | 0.934008 | 0.065992 |
| 1.35 | 0.943762 | 0.056238 |
| 1.40 | 0.952285 | 0.047715 |
| 1.45 | 0.959695 | 0.040305 |
| 1.50 | 0.966105 | 0.033895 |
| 1.60 | 0.976348 | 0.023652 |
| 1.70 | 0.983790 | 0.016210 |
| 1.80 | 0.989091 | 0.010909 |
| 1.90 | 0.992790 | 0.007210 |
| 2.00 | 0.995322 | 0.004678 |
| 2.20 | 0.998137 | 0.001863 |
| 2.40 | 0.999311 | 0.000689 |
| 2.60 | 0.999764 | 0.000236 |
| 2.80 | 0.999925 | 0.000075 |
| 3.00 | 0.999978 | 0.000022 |