5-2 大陸の地殻熱流量モデル -- 定常熱伝導方程式
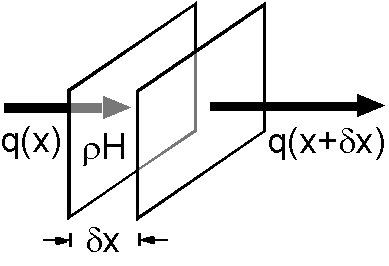
1次元定常熱伝導方程式: 図のような2つの平行な面の間の熱流量について考えます.面に垂直に \(x\) 軸を取り,1つの面から入る熱流量を \(q(x)\),微小距離 \(\delta x\) 離れた他方の面から出る熱流量を \(q(x+\delta x)\) とします.すると熱流量の差は次式で近似できます. \[ q(x+\delta x) - q(x) = \frac{dq}{dx} \delta x. \] この式の右辺に,温度を \(T\),熱伝導度を \(k\) として \(q=-k\frac{dT}{dx}\) を代入して整理すると, \[ q(x+\delta x) - q(x) = -k\frac{d^2T}{dx^2}\delta x, \] となります.いま,温度は距離だけに依存し,時間には一定の定常状態を考えます(非定常の熱伝導は次ページで扱います).すると,この熱流量の差は2つの面の間にある熱源から補充されることとなります.図で,単位面積の2つの面の間の体積は \(\delta x\) です.また,熱源の単位質量当たりの発熱量を \(H\) とすると,単位体積当たりの発熱量は密度を \(\rho\) として \(\rho H\) です.よって, \begin{eqnarray} -k\frac{d^2T}{dx^2}\delta x & = & \rho H\delta x, \nonumber \\ \frac{d^2T}{dx^2} & = & -\frac{\rho H}{k}. \label{eq01} \end{eqnarray} となり,これは1次元定常熱伝導方程式とよばれます.
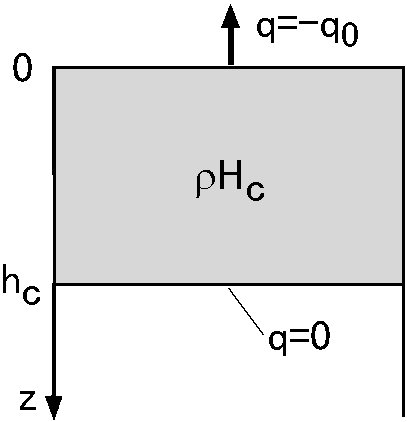
大陸の地殻熱流量モデル: 地殻熱流量や地下温度分布は式 (1) を積分して得られます.大陸のモデルとして,図のような単位質量当たり発熱量 \(H_c\) の発熱源が一様に分布する,密度 \(\rho\) 厚さ \(h_c\) の地殻を考えます.地表を原点とし深さ方向に座標軸 \(z\) を取り,熱流量は地表で \(q=-q_0\)(負記号は熱流が上向きのため),地殻の底で \(q=0\) とします.式 (1) の熱伝導方程式は, \[ k\frac{d^2T}{dz^2} = -\rho H_c, \] となります.これを積分すると,積分定数を \(C\) として次式を得ます. \[ k\frac{dT}{dz} = -\rho H_c z + C. \] 地表では, \(\left[-k\frac{dT}{dz}\right]_{z=0}=-q_0\) より \(C=q_0\) となり,熱流量は次式で表わされます. \[ q = -k\frac{dT}{dz} = -q_0 + \rho H_c z. \] 地殻の底で \(q=0\) より \(H_c\) と \(h_c\) の次の関係が得られます. \[ \rho H_c h_c = q_0. \] この関係式に大陸地域での典型的な値, \(q_0\) = 65 mW/m2 と \(\rho H_c\) = 2 μW/m3 を代入し, \(h_c\) = 32.5 km と妥当な値を得ます.地下温度分布は, \(dT/dz\) を更に積分し,地表の温度を \(T_0\) として, \[ T = T_0 + \frac{q_0}{k}z - \frac{\rho H_c}{2k}z^2, \] となります. \(z\) に \(h_c\) を代入し,上の \(\rho H_ch_c\) = \(q_0\) の関係を用い, \(k\) = 3.5 W/m K とすると,地殻の底の温度も次のように妥当な値となります. \[ T(h_c) = T_0 + q_0 h_c/2k \approx T_0 + 302\ °\mathrm{C}. \]
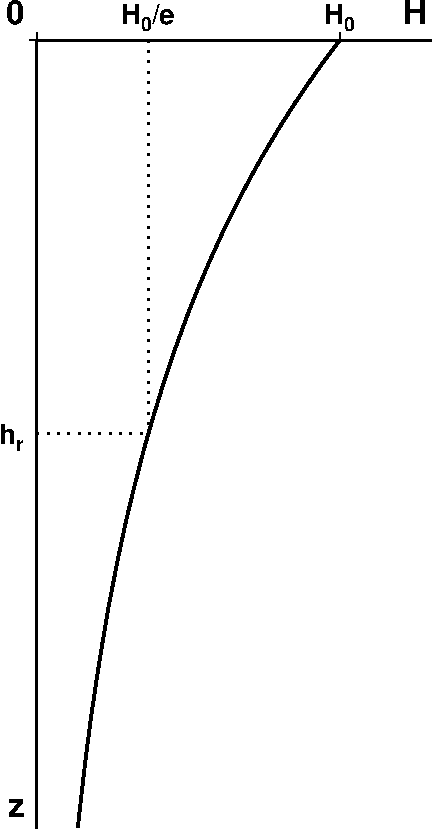
しかし,上のモデルではマントルからの熱流が考慮されていません.また,前ページで扱ったように,発熱源は浅い領域ほど多くなります.そこで,図のように発熱源の分布が深さの指数関数で減少するモデルを考え,単位質量当たりの発熱量 \(H\) を, \begin{equation} H = H_0 e^{-z/h_r}, \label{eq02} \end{equation} で表わします.ここに, \(H_0\) と \(h_r\) は発熱量の地表の値と 1/\(e\) に減少する深さです.熱伝導方程式は次式となります. \begin{equation} k\frac{d^2T}{dz^2} = -\rho H_0 e^{-z/h_r}, \label{eq03} \end{equation} これを解くための境界条件として,マントルからの熱流量が \(z=\infty\) で \(q=-q_m\) とします.式 (3) を積分して, \[ k\frac{dT}{dz} = \rho H_0 h_r e^{-z/h_r} + C, \] となりますが,積分定数 \(C\) は \(z=\infty\) で \(q=-q_m\) から, \[ \left[-k\frac{dT}{dz}\right]_{z=\infty} = -C = -q_m, \] より \(C=q_m\) ですので,熱流量を表わす式は次のようになります. \begin{equation} q = -k\frac{dT}{dz} = -q_m - \rho H_0 h_r e^{-z/h_r}. \label{eq04} \end{equation} 地表での熱流量 \(q=-q_0\) は \(z=0\) とおいて, \begin{equation} q_0 = q_m + \rho H_0 h_r, \label{eq05} \end{equation} となります.この式は地表で観測される熱流量 \(q_0\) と地表付近の岩石の発熱量 \(H_0\) が直線関係にあることを示します.地下温度分布はさらに \(dT/dz\) を積分し,地表の温度を \(T_0\) とすることで次式となります. \begin{equation} T = T_0 + \frac{q_m}{k}z + \frac{\rho H_0 h_r^2}{k}(1 - e^{-z/h_r}). \label{eq06} \end{equation}
このモデルの優れた点は,式 (5) が大陸での観測結果をよく説明することです.地殻熱流量が大きい地点では,地下の岩石の発熱量も大きいという直線関係が観測されています.そのデータから,マントルからの熱流量 \(q_m\) として 20~30 mW/m2 の値が得られています.また, \(h_r\) としては 7~10 km 程度となり,発熱源が上部地殻に集中していることを示します.式 (6) も大陸の地下温度分布をよく表わすと考えられています.例えば, \(q_m\) = 30 mW/m2, \(h_r\) = 10 km, \(q_0\) = 65 mW/m2, \(\rho H_0\) = 2 μW/m3, \(k\) = 3.5 W/m K を代入すると \(z\) = 30 km での温度は \(T_0\)+311 °C となります.
このように,大陸で観測される地殻熱流量は地下上層部に発熱源が集中しているモデルで良く説明されます.そのため歴史的には,発熱源の少ない地殻からなる海洋地域では地殻熱流量は小さいと考えられてきました.しかし観測が始まると,海洋地域の熱流量のほうがむしろ大きいことが判明しました.これは,海洋地域のリソスフェアが大陸地域のそれよりも格段に若く現在も冷却の途中にあり,冷却過程の熱伝導による熱移送が大きいためです.即ち,海嶺に上昇してきた高温のマントル物質が,冷却しながら海洋底拡大により移動する際のリソスフェア内の熱伝導で説明されます.海洋リソスフェアの熱流量モデルについては,後のページで扱います.
球の熱伝導モデル: 半径 \(a\) の球の内部に単位質量当たりの発熱量 \(H\) の発熱源が一様に分布しているときの球表面での単位面積当たりの熱流 \(q_0\) を考えてみます.但し,温度は時間で一定で定常状態にあるとします.球内部で単位時間あたりに発生する熱エネルギーは球の密度を \(\rho\) として, \[ (4/3)\pi a^3\rho H, \] です.この熱は,エネルギー保存則から球表面から放出される熱, \[ 4\pi a^2 q_0, \] と等しくなります.よって,球表面からの熱流は次のようになります. \[ q_0 = \rho Ha/3. \]
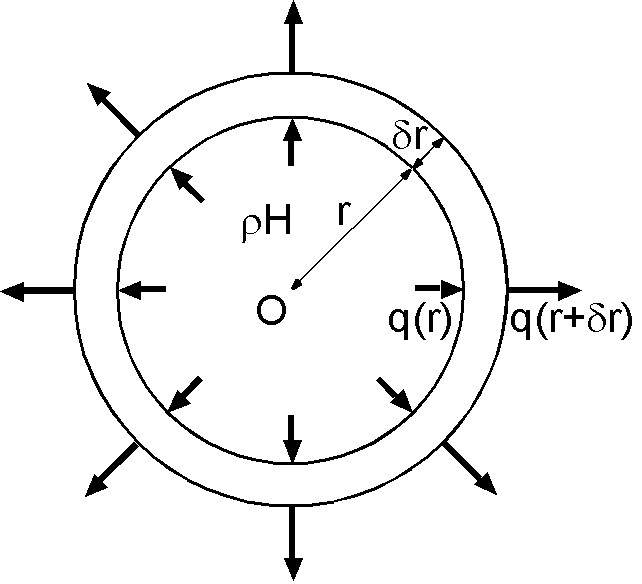
発熱源が一様分布でないときは,問題はこのように簡単ではありません.しかし,発熱源の分布が球中心からの距離 \(r\) だけによるときは,以下のように1次元の問題として扱うことができます.図は球内部の発熱源による熱流が,半径が \(r\) と \(r+\delta r\) の間の微小厚さの球殻に \(q(r)\) で流入し, \(q(r+\delta r)\) で流出する様子を示します.出入りする熱流の差は次式で近似できます. \[ q(r+\delta r) - q(r) = \frac{dq(r)}{dr}\delta r. \] この近似式を用いて球殻全体についての熱流の差を近似しますが,次のように \(\delta r\) の2次の項は省略します. \begin{eqnarray*} & & 4\pi(r+\delta r)^2 q(r+\delta r) - 4\pi r^2 q(r) \\ & \approx & 4\pi\left[(r^2+2r\delta r)\left(q(r)+\frac{dq(r)}{dr}\delta r\right) - r^2q(r)\right], \\ & \approx & 4\pi r^2\left(\frac{dq(r)}{dr} + \frac{2}{r}q(r)\right)\delta r. \end{eqnarray*} この球殻から流出する熱は,球の温度が一定の定常状態では,球殻内部の熱源による熱, \[ 4\pi r^2\rho H\delta r, \] と等しくなります.よって,次の関係式 \[ \frac{dq}{dr} + \frac{2}{r}q = \rho H, \] を得ますが,左辺を次のように変形すると便利です. \[ \frac{1}{r^2}\frac{d}{dr}\left(r^2 q\right) = \rho H. \] この式に, \(k\) を熱伝導度として \(q=-k\frac{dT}{dr}\) を代入し次式となります. \begin{equation} \frac{1}{r^2}\frac{d}{dr}\left(r^2 \frac{dT}{dr}\right) = -\frac{\rho}{k} H. \label{eq07} \end{equation} この式が熱源分布が半径方向だけに依存する球の熱伝導方程式です.
発熱源が一様分布している球について,球内部の温度分布を式 (7) から導いてみます. \(H\) は定数ですので,式 (7) を2回積分し積分定数を \(C_1\), \(C_2\) とすると, \[ T = -\frac{\rho H}{6k}r^2 - \frac{C_1}{r} + C_2, \] となりますが,球の中心で温度 \(T\) が有限である条件から \(C_1=0\) となり,球表面の温度を \(r=a\) で \(T=T_0\) として \(C_2\) を決めると, \begin{equation} T = T_0 + \frac{\rho H}{6k}(a^2 - r^2), \label{eq08} \end{equation} となり,温度は球の中心に近づくほど上昇することが分かります.この式を微分して, \begin{equation} q = -k\frac{dT}{dr} = \frac{\rho H}{3}r, \label{eq09} \end{equation} が熱流量を与えます.この式から球表面の熱流量 \(q_0\) は \[ q_0 = \rho Ha/3, \] となり,前述のエネルギーバランスからの結果と一致します.
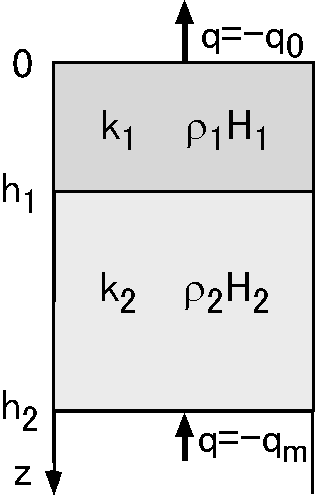
問題5-2-1
大陸の地殻熱流量を2層構造モデルで考えます.第1層の底面の深さを \(h_1\),熱伝導度を \(k_1\),密度を \(\rho_1\),単位質量当たり発熱量を \(H_1\) とし,第2層についてはそれぞれ \(h_2\), \(k_2\), \(\rho_2\), \(H_2\) とします.地表を原点とし深さ方向に \(z\) 軸をとり,地表の熱流量が \(-q_0\),マントルからの熱流量が第2層の底で \(-q_m\) とします.また,地表の温度を \(T_0\) とします.
(1) 地殻熱流量と地下温度分布を与える以下の式を導きなさい. \begin{eqnarray*} q & = & -q_0 + \rho_1H_1z \quad (0\leq z\leq h_1), \\ T & = & T_0 + \frac{q_0}{k_1}z - \frac{\rho_1H_1}{2k_1}z^2 \quad (0\leq z\leq h_1), \\ q & = & -q_m + \rho_2H_2(z - h_2) \quad (h_1\leq z\leq h_2), \\ T & = & T_0 + \left(\frac{q_0}{k_1}-\frac{q_m}{k_2}\right)h_1 - \frac{\rho_2H_2}{k_2}h_1h_2 + \left(\frac{\rho_2H_2}{k_2}-\frac{\rho_1H_1}{k_1}\right)\frac{h_1^2}{2} \\ & & + \frac{q_m + \rho_2H_2 h_2}{k_2}z - \frac{\rho_2H_2}{2k_2}z^2 \quad (h_1\leq z\leq h_2). \end{eqnarray*}
(2) \(h_1\) = 10 km, \(h_2\) = 40 km, \(k_1\) = \(k_2\) = 3 W/m K, \(\rho_1H_1\) = 2.5 μW/m3, \(\rho_2H_2\) = 0.5 μW/m3, \(q_m\) = 25 mW/m2, \(T_0\) = 0 °C とするとき,地表の熱流量 \(q_0\) と第1層,第2層の底の温度 \(T_1\), \(T_2\) を求めなさい.
問題5-2-2
発熱源が一様分布している球の温度と熱流量の分布はそれぞれ本文の式 (8) と (9) で表わされます.これを地球に適用し,球表面の熱流量を 80 mW/m2,半径を6400 km,熱伝導度を4 W/mK,表面温度を0°C として中心温度を求めなさい.
問題5-2-3
単位質量当たりの発熱量 \(H\) が \[ H = H_0\left(\frac{r}{a}\right)^n \] で表わされる球の熱伝導モデルを考えます.ここに,\(a\), \(r\), \(H_0\) はそれぞれ球の半径,中心からの距離,球表面での発熱量で,\(n\) は \(r\) に依存しない定数です.
(1) 球内部の温度 \(T\) と熱流量 \(q\) の分布は球の密度と熱伝導度を \(\rho\) と \(k\),表面の温度を \(T_0\) として次式で表わされることを導きなさい. \begin{align*} T & = T_0 + \frac{\rho H_0a^2}{(n+2)(n+3)k}\left(1 - \left(\frac{r}{a}\right)^{n+2}\right), \\ q & = \frac{\rho H_0a}{n+3}\left(\frac{r}{a}\right)^{n+1}. \end{align*}
(2) モデルを地球に適用し,\(q_0\) = 80 mW/m\(^2\), \(a\) = 6400 km, \(k\) = 4 \(\mathrm{W/m\,K}\), \(T_0\) = 0°C として \(n\) = 2 のときの中心温度を求めなさい.
参考文献:
- Turcotte, D. & G. Schubert, Geodynamics (Second Edition), 456 pp., Cambridge University Press, 2002.