物理地学の基礎：演習問題と解説

３-３ アイソスタシー

地球楕円体が，流体地球が自転するときの形に近いことから，固体の地球も地質学的時間スケールで作用する力に対しては流体として振舞うと考えられることは前述しました．一方で，山岳地域での重力調査から，高い山の地下には深い根があることが分かってきました．これは海上に浮かぶ氷山のように，比較的軽い山体がより重いマントルに深くまで位置することで，重力的に釣合うと考えられます．このような釣合の状態をアイソスタシー（地殻の均衡）とよびます．そのため，一般にある程度大きな地質構造ではアイソスタシーが成り立っています．

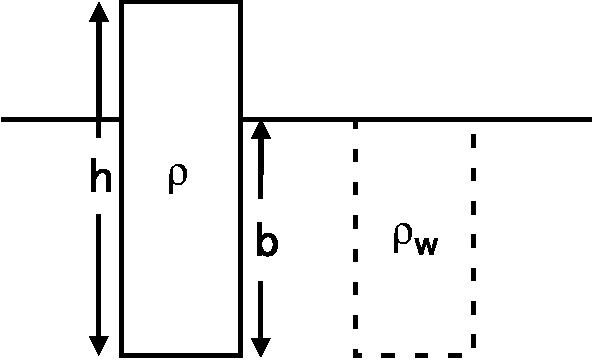
アイソスタシーとアルキメデスの原理

アイソスタシーとアルキメデスの原理： アイソスタシーは水に木片が浮かぶ原理と同じと考えられています．図で，木片と水の密度をそれぞれ \(\rho\) と \(\rho_w\)，木片の全高と水に沈んでいる部分の高さをそれぞれ \(h\) と \(b\) とします．木片の底より下の適当な水平面では圧力がどこでも同じで，この面を補償面とよびます．ここで，補償面を木片の底の深さに取れば， \[ \rho h = \rho_w b, \] が成り立ちます．これより，水面より上の木片の高さは， \[ h - b = h - \frac{\rho}{\rho_w}h = h\left(1 - \frac{\rho}{\rho_w}\right), \] で与えられます．木片と水の密度比は 0.5 程度ですので，木片全高の半分程度が水面より上となりますが，氷の場合は 10% 程度しか水面上には現れません．

この考えを大陸地殻とマントルに当てはめると，地殻の厚さと密度をそれぞれ 30 km と 2700 kg/m3，マントルの密度を 3300 kg/m3 として，地殻上面はマントル表面から 5.5 km 上の状態でマントルに浮いていることになります．しかし実際の地球では，厚さ 30~50 km の軽い大陸地殻と，厚さ 7 km 程度の薄くてより重い海洋地殻が (厚さ約 4 km の海洋を載せて)，更に重いマントルの全表面を覆っており，マントル表面が見えるわけではありません．なお，地球は深さとともに温度と圧力が増し，マントルの密度も深さとともに増大し，核-マントル境界付近では約 5500 kg/m3 になりますが，ここでは地殻付近の値の 3300 kg/m3 を使用します．

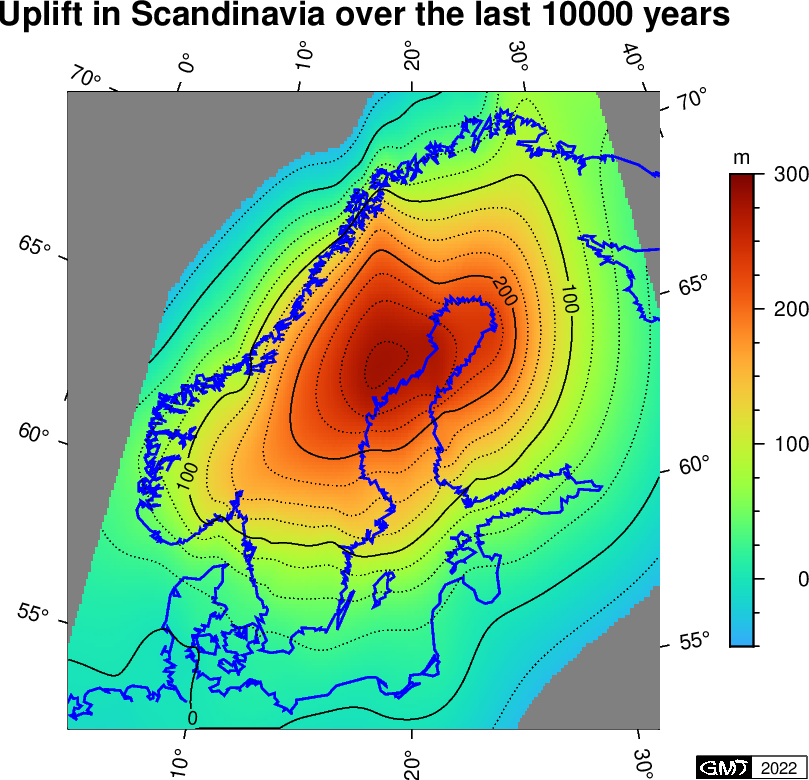
スカンディナビアの１万年前からの隆起
Click to enlarge

アイソスタシーの証拠： 最終氷期が終わると高緯度地域では氷床が短時間で消失し，その重さで沈んでいた地殻のゆっくりした隆起が始まりました．その際，隆起の進行とともに海岸線の痕跡が縞状に残ります．過去の海岸線に見られる化石のC-14年代から，地殻の隆起の時間変化が分かります．代表的な例のスカンジナビア半島では現在も最大年間1 cmで隆起が続いています．右図は Passe & Daniels (2015) に基づき， GMT (Generic Mapping tools) で求めたスカンジナビア半島の過去１万年間の隆起の分布です．最大で 280 m の隆起が見られますが，その場所は氷期には最も沈んでいたことになります．なお，負の隆起を示す周辺地域も見られますが，氷床の周辺地域の地殻は隆起ではなく沈降するようです．それは，氷床の周辺の地殻は氷床の重さで力学的に上方に曲げられていたため，氷床消失後は元に戻るためです．

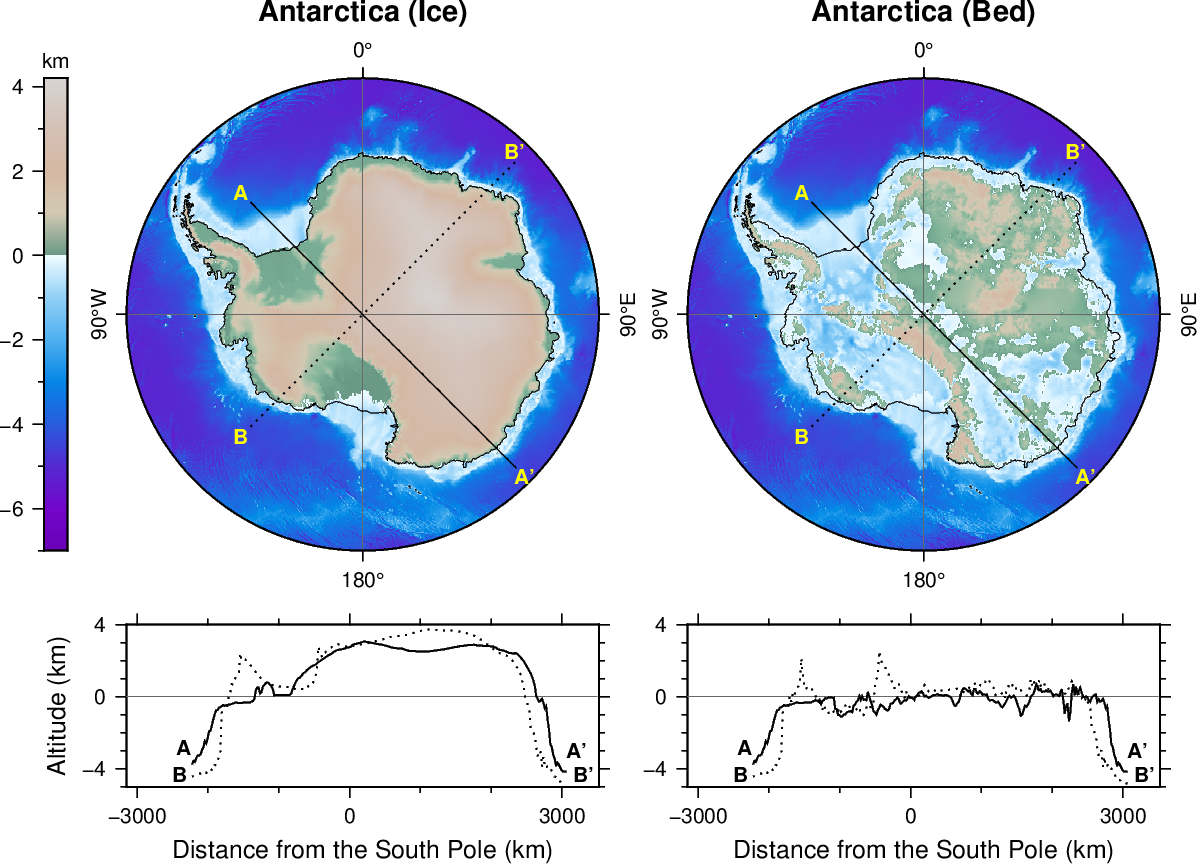
南極大陸の陸地の平均高度が異常に低いこともアイソスタシーの証拠です．南極大陸の氷床と陸地の高度分布を， NCEI (National Centers for Environmental Information) の全球地形データベース ETOPO1 を使用して GMT により表わした図を下に示します．図（左上）の通常の地図からは南極大陸の海抜が高いこと，図（左下）の２測線の断面からは多くの地域で高度 2〜3 km であることが分かります．これは図が大陸を覆う厚い氷床の高度を表わしているからです．一方，図（右）は氷床を取り除いた陸地部分の地図と断面図です．これらの図から分かる通り，南極大陸の陸地はかなりの領域が海面下となっています．陸地の全球での平均高度は 840 m と言われているので，南極大陸は氷床の重さで沈みアイソスタシーが成立していると考えられます．

南極大陸の氷床と陸地の高度分布，及び断面図
Click to enlarge

↑ ページ冒頭

マントルの流動性： アイソスタシーは固体の岩石であるマントルが流体の性質を示す例です．前述の通り，氷床の重さで沈んでいたスカンジナビア半島は，現在でも最大で 1 cm/yr の割合で隆起が続いていて，これからマントルの粘性率が推定されています．粘性率の詳細はここでは省略しますが，物質の粘度を表す定数で，一般に記号 \(\mu\) で表します．単位は [Pa s] で，値が大きいほど流れにくいことを示します (Pa は圧力の単位で N/m2 です)．スカンジナビア半島が１万年間に約 280 m 隆起した記録から，マントルの粘性率は次のように推定されています． \[ \mu = 10^{21}\ \mathrm{Pa\,s}. \] 参考のために各種物質の粘性率 \(\mu\) を，後述する熱拡散率 \(\kappa\) とともに表に示します（Turcotte & Schubert 2002, Table 6-1 より）．

物質\(\mu\ \mathrm{[Pa\,s]}\)\(\kappa\ \mathrm{[m^2/s]}\)
空気\(1.78\times 10^{-5}\)\(2.02\times 10^{-5}\)
水\(1.14\times 10^{-3}\)\(1.40\times 10^{-7}\)
オリーブ油\(0.099\)\(9.2\times 10^{-8}\)
グリセリン\(2.33\)\(9.8\times 10^{-8}\)

この表で物質の違いによる粘性率 \(\mu\) の違いは経験上得られる感覚とよく合っていますが，マントルの 1021 Pa s という大きな値からマントルが流動するかどうかの判断は困難です．

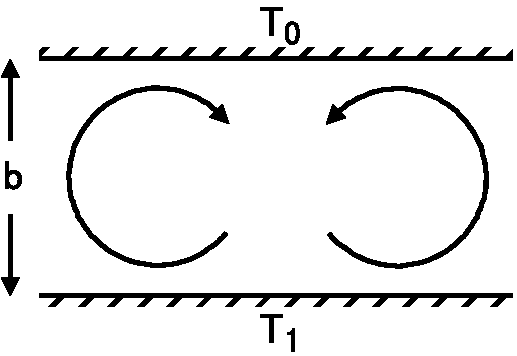
下面を加熱した流体の２次元対流モデル

マントル対流： マントルが流動することは，流体力学におけるレイリー数 \(Ra\) を見積もることで示されています．以下はレイリー数 \(Ra\) を用いた理論の平易な説明です．いま，横方向に無限に広がった，厚さ \(b\) の流体層を下から熱し，上面と下面をそれぞれ温度 \(T_0\) と \(T_1\) に保つとします (\(T_0<T_1\))．下面と上面の温度差 \(T_1-T_0\) が小さいうちは対流は起こらずに熱伝導のみで熱が下面から上面に伝わりますが，温度差がある限界を越えると対流が発生し，より効率的に熱が運ばれると考えられます．また，対流が発生するかどうかは温度差だけではなく，流体層の厚さや流体の物理的性質にも依存すると考えられます．流体力学では，対流の発生のしやすさを示す無次元のパラメータとして，次式で与えられるレイリー数が定義されました． \[ Ra = \frac{\rho_0 g\alpha_v(T_1 - T_0)b^3}{\mu\kappa}. \] ここに， \(\rho_0\) は温度 \(T_0\) での密度， \(g\) は重力加速度です． \(\alpha_v\) は体積膨張率で， 1 K の温度上昇で体積 \(v\) が膨張する割合を表し， \(\alpha_v = \frac{1}{v}\left(\frac{dv}{dT}\right)\) で与えられます．また， \(\kappa\) は熱拡散率とよばれ，値が大きいほど熱が拡散しやすく，熱伝導率 \(k\) を密度 \(\rho\) と比熱 \(c\) で割ったもので， \(\kappa = k/\rho c\) で与えられます．レイリー数 \(Ra\) の式に含まれる各変数を観察すると，分子では値が大きいほど，分母では値が小さいほど，対流が発生しやすくなることが直感的に理解できます．理論と実験の研究結果から，一般にはレイリー数 \(Ra\) が 1000 を越えると対流が発生すると判断して良いことが分かります．

例として厚さ 10 cm のオリーブ油の層を，下面と上面の温度差を 1°C に保つ場合のレイリー数を計算してみます． \(\rho_0\) = 1000 kg/m3， \(g\) = 10 m/s2， \(\alpha_v\) = 0.001 K-1， \(T_1-T_0\) = 1 K， \(b\) = 0.1 m， \(\mu\) = 0.1 Pa s， \(\kappa\) = 1\(\times\)10-7 m2/s を代入すると， \(Ra\) = 1\(\times\)106 となり，このようなわずかな温度差でも対流が発生することがわかります．一方，岩石の場合には普通の感覚では粘性は考えられませんが，仮に粘性率がマントルの値程度であったとして， \(\mu\) = 1021 Pa s と極めて大きいので， \(Ra\) は極めて小さい値となり，対流が発生するはずがないことが示されます．

しかし，これを地球規模で考えるとそうでもないことが分かります．粘性率 \(\mu\) が大きくても \(T_1-T_0\) や \(b^3\) が大きいので，マントルのレイリー数 \(Ra\) は 10\(^5\)-10\(^7\) に達し，対流が発生するべき値となります（問題3.3.3）．

↑ ページ冒頭

問題３-３-１

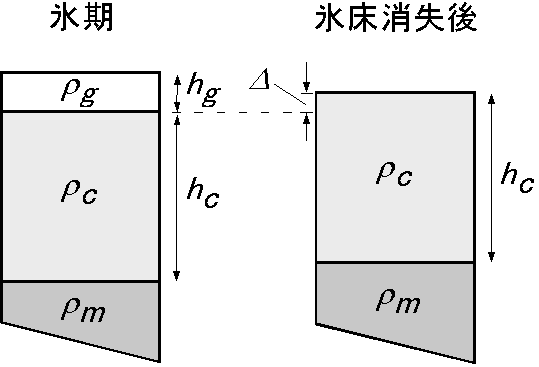
氷床消失後のアイソスタシーによる地殻の隆起

図左は厚さ \(h_c\)，密度 \(\rho_c\) の大陸地殻が厚さ \(h_g\)，密度 \(\rho_g\) の氷床の重さで沈んでいる様子を，図右は氷床消失後に大陸地殻が \(\mit\Delta\) 隆起した様子を示します．ここで， \(\rho_g\), \(\rho_c\), マントルの密度 \(\rho_m\) をそれぞれ kg/m3 の単位で， 900, 2700, 3300 として次の問いに答えなさい．

（１） 現在も上昇が続くスカンジナビア半島は厳密にはアイソスタシーは達成されていませんが，ここではアイソスタシーの均衡にあるとします．氷床の消失後に地殻が 300 m 隆起したとして，氷期におけるスカンジナビア半島の氷床の厚さを求めなさい．

（２） 南極大陸の氷床の厚さを 2500 m として，氷床が消失しアイソスタシーが成立したときの大陸の隆起量を求めなさい．但し，氷床が溶けることによる海面の上昇は考慮しないとします．

→ 解答

問題３-３-２

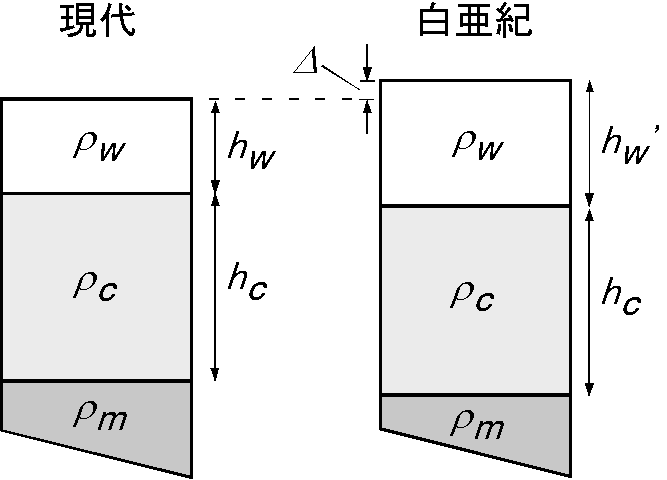
白亜紀の海面上昇とアイソスタシーによる海底の沈降

温暖期の白亜紀には海水準が現代よりも 200〜300 m も高く，増大した海洋の重さで海洋地殻は沈降しました．従って，実際の海洋の深さは海水準が上昇した高さよりもさらに深くなっていました．白亜紀にもアイソスタシーが成立するとして，白亜紀の海洋の深さ \(h_w^\prime\) と現代の海洋の深さ \(h_w\) の差を表す次の式を導きなさい．但し，現代と白亜紀の海水準の差を \(\mit\Delta\)，地殻の厚さを現代も白亜紀も同じ \(h_c\)，海水，地殻，マントルの密度をそれぞれ \(\rho_w\)， \(\rho_c\)， \(\rho_m\) とします． \[ h_w^\prime - h_w = \frac{\rho_m}{\rho_m - \rho_w}\mit\Delta. \] 次に，海水準の差 \(\mit\Delta\) を 200 m とし，海水の密度 \(\rho_w\) とマントルの密度 \(\rho_m\) をそれぞれ 1000 kg/m3 と 3300 kg/m3 とすると， \(h_w^\prime - h_w\) は何 m か?

→ 解答

問題３-３-３

上部マントルのレイリー数を，\(\rho_0\) = 4000 kg/m3，\(g\) = 10 m/s2，\(\alpha_v\) = 3\(\times\)10-5 K-1，\(T_1-T_0\) = 1500 K，\(b\) = 700 km，\(\mu\) = 1021 Pa s，\(\kappa\) = 10-6 m2/s として計算しなさい．

さらにマントル全体を考えて，\(b\) = 2900 km，\(T_1-T_0\) = 3000 K としてマントル全体での値も求めなさい．

→ 解答

参考文献：

↑ ページ冒頭   ← 前ページ   → 次ページ