重力ポテンシャルから求める地球の扁平率

地球の扁平率を求めた問題３-５-１の補足として，より高い近似レベルの重力ポテンシャルを用いる方法を， Stacey (1992) に基づいて以下に解説します．

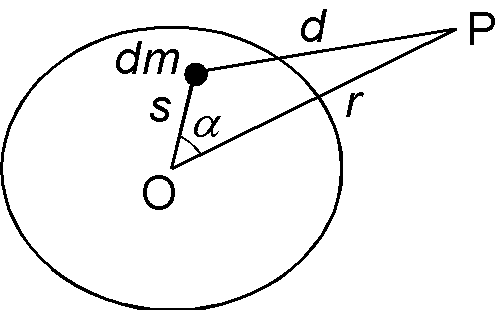
地球を密度一様で質量 \(M\) の回転楕円体とし，その中心を原点 O とします．いま，地表を含む地球外の点 P の重力ポテンシャル \(V_m\) を考えます．地球内部の微小体積の質量を \(dm\) とし，図のように距離や角度のパラメータを取ります． \(V_m\) は \(dm\) による重力ポテンシャルを地球全体で積分し，万有引力定数を \(G\) として次式となります． \begin{equation} V_m = -G\int\frac{dm}{d}, \label{eq01} \end{equation} ここで \(d\) を余弦定理で \(r\), \(s\), \(\alpha\) で表わし \(1/r\) で展開し近似します．これをマッカラーの公式（MacCullagh's formula）といいます． \begin{eqnarray} V_m & = & -G\int\frac{1}{\sqrt{r^2 + s^2 - 2rs\cos\alpha}}dm, \nonumber \\ & = & -\frac{G}{r}\int\left(1 + \frac{s^2}{r^2} -2\frac{s}{r}\cos\alpha\right)^{-\frac{1}{2}}dm, \nonumber \\ & = & -\frac{G}{r}\int\left[1 - \frac{1}{2}\left(\frac{s^2}{r^2} -2\frac{s}{r}\cos\alpha\right) + \frac{3}{8}\left(\frac{s^2}{r^2} -2\frac{s}{r}\cos\alpha\right)^2 - \cdots\right]dm, \nonumber \\ & = & -\frac{G}{r}\int\left(1 + \frac{s}{r}\cos\alpha - \frac{1}{2}\frac{s^2}{r^2} + \frac{3}{2}\frac{s^2}{r^2}\cos^2\alpha + \cdots\right)dm, \nonumber \\ & = & -\frac{G}{r}\int\left(1 + \frac{s}{r}\cos\alpha + \frac{s^2}{r^2} - \frac{3}{2}\frac{s^2}{r^2}\sin^2\alpha + \cdots\right)dm, \nonumber \\ & \approx & -\frac{G}{r}\int dm - \frac{G}{r^2}\int s\cos\alpha dm - \frac{G}{r^3}\int s^2 dm + \frac{3}{2}\frac{G}{r^3}\int s^2\sin^2\alpha dm. \label{eq02} \end{eqnarray} この \(V_m\) の式 (2) は４つの積分からなり，それぞれを以下のように変形していきます．

第１項は質量 \(M\) が地球の中心に集中しているときのポテンシャルで次式となります． \begin{equation} -\frac{G}{r}\int dm = -\frac{GM}{r}. \label{eq03} \end{equation}

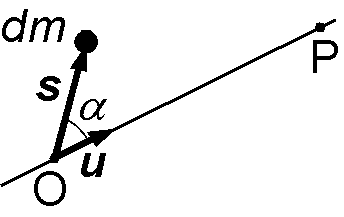
第２項については，右図のように地心直交座標系で O から \(dm\) へ向かうベクトルを \({\bf s} = (x,y,z)\)， OP 軸上の単位ベクトルを \({\bf u} = (u_x,u_y,u_z)\) とすると， \begin{eqnarray*} \int s\cos\alpha dm & = & \int {\bf s}\cdot{\bf u}dm = \int (xu_x + yu_y + zu_z) dm, \\ & = & u_x\int x dm + u_y\int y dm + u_z\int z dm. \end{eqnarray*} これらの積分は \(x, y, z\) が地心直交座標系の原点に関して対称なため全てゼロとなります．または，原点が地球の重心であるためと考えても良いです．即ち， \begin{equation} - \frac{G}{r^2}\int s\cos\alpha dm = 0. \label{eq04} \end{equation}

第３項については，積分を次のように変形します． \begin{eqnarray*} \int s^2 dm & = & \int(x^2 + y^2 + z^2)dm, \\ & = & \frac{1}{2}\left(\int(y^2+z^2)dm + \int(z^2+x^2)dm + \int(x^2+y^2)dm\right). \end{eqnarray*}

これら３つの積分は順に x 軸， y 軸, z 軸の回りの慣性モーメントです．右図に微小質量 \(dm\) の z 軸の回りの慣性モーメント， \(h^2dm=(x^2+y^2)dm\) を示しましたが，これを地球全体に積分すると地球の z 軸（自転軸）の回りの慣性モーメントになります．これら３軸 x， y， z の回りの慣性モーメントは慣習としてそれぞれ， \(A, B, C\) と表わします．また，ここでは z 軸の回りの回転対称を考えてますので \(A=B\) です．結局，第３項は次のようになります． \begin{equation} -\frac{G}{r^3}\int s^2 dm = -\frac{G}{2r^3}(2A + C). \label{eq05} \end{equation}

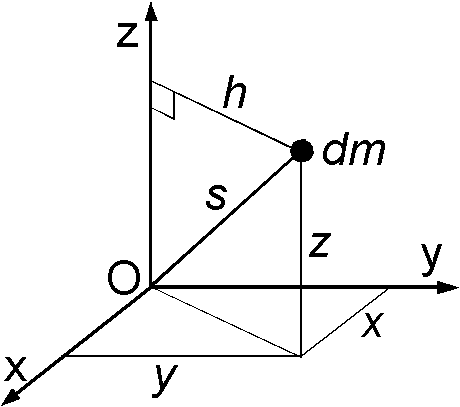
第４項の積分は OP 軸の回りの慣性モーメントですが，次のように地心直交座標で表して展開します． \begin{eqnarray*} \small{\int s^2\sin^2\alpha dm} & = & \small{\int\left(|{\bf s}|^2 - ({\bf s}\cdot{\bf u})^2\right)dm = \int\left(x^2+y^2+z^2 - (xu_x+yu_y+zu_z)^2\right)dm}, \\ & = & \small{\int(x^2 + y^2 + z^2 - x^2u_x^2 - y^2u_y^2 - z^2u_z^2 - 2xyu_xu_y - 2yzu_yu_z - 2zxu_zu_x)dm}. \end{eqnarray*} これを， \(u_x^2\) + \(u_y^2\) + \(u_z^2\) = 1 より \(u_x^2\) = 1 - \(u_y^2\) - \(u_z^2\) とし， \(u_y^2\) と \(u_z^2\) についても同様にして変形すると， \begin{eqnarray*} \int s^2\sin^2\alpha dm & = & u_x^2\int(y^2+z^2)dm + u_y^2\int(z^2+x^2)dm + u_z^2\int(x^2+y^2)dm \\ & & \qquad\qquad - 2u_xu_y\int xydm - 2u_yu_z\int yzdm - 2u_zu_x\int zxdm, \end{eqnarray*} となりますが，前半の３つの積分は \(x,y,z\) 軸の回りの慣性モーメント \(A,B,C\) であり，後半の３つの積分は原点の回りの対称性からゼロです．よって， OP 軸の回りの慣性モーメントは次式となります． \[ \int s^2\sin^2\alpha dm = Au_x^2 + Bu_y^2 + Cu_z^2, \] さらに \(A=B\) とし， \(u_z\) を点 P の緯度 \(\phi\) で \(u_z=\sin\phi\) と表わすと，第４項は次式となります． \begin{equation} \frac{3}{2}\frac{G}{r^3}\int s^2\sin^2\alpha dm = \frac{3}{2}\frac{G}{r^3}\left(A + (C-A)\sin^2\phi\right). \label{eq06} \end{equation}

↑ ページ冒頭

式 (3)〜(6) の結果を式 (2) に代入し整理すると，点 P(\(r\),\(\phi\)) での次の重力ポテンシャルとなります． \begin{eqnarray} V_m & = & -\frac{GM}{r} - \frac{G}{2r^3}(2A + C) + \frac{3}{2}\frac{G}{r^3}\left(A + (C-A)\sin^2\phi\right), \nonumber \\ & = & -\frac{GM}{r} + \frac{G}{r^3}(C-A)\left(\frac{3}{2}\sin^2\phi - \frac{1}{2}\right). \label{eq07} \end{eqnarray} さらに，自転の遠心力も考慮した重力ポテンシャル \(V\) は自転の角速度を \(\omega\) として次式となります． \begin{equation} V = -\frac{GM}{r} + \frac{G}{r^3}(C-A)\left(\frac{3}{2}\sin^2\phi - \frac{1}{2}\right) - \frac{1}{2}\omega^2r^2\cos^2\phi. \label{eq08} \end{equation}

式 (8) の重力ポテンシャルが赤道（\(r=a\)）と極（\(r=b\)）で等しいと置き変形すると， \begin{eqnarray*} -\frac{GM}{a} - \frac{G}{2a^3}(C-A) - \frac{1}{2}\omega^2a^2 & = & -\frac{GM}{b} + \frac{G}{b^3}(C-A), \\ -\frac{1}{a} - \frac{C-A}{2Ma^3} - \frac{\omega^2a^2}{2GM} & = & -\frac{1}{b} + \frac{C-A}{Mb^3}, \end{eqnarray*} これより地球の扁平率 \(f\) は， \[ f = 1 - \frac{b}{a} = \frac{C-A}{Ma^2}\left(\frac{a^2}{b^2} + \frac{b}{2a}\right) + \frac{\omega^2a^2b}{2GM}, \] となりますが， \(a\) と \(b\) の差は僅かですので右辺で次の近似を行います． \[ \frac{a^2}{b^2} \approx 1, \quad \frac{b}{a} \approx 1, \quad a^2b = a^3\frac{b}{a} \approx a^3. \] 結局，扁平率の近似式は次のようになります． \begin{equation} f \approx \frac{3}{2}\frac{C-A}{Ma^2} + \frac{1}{2}\frac{\omega^2a^3}{GM}. \label{eq09} \end{equation} この式の \((C-A)/Ma^2\) は慣性モーメントの差と \(Ma^2\) の比で，重力から見た地球の扁平度を表わし，慣習として \(J_2\) と表わします． \(J_2\) は人工衛星の軌道変化から決定され，その値は次の通りです． \begin{equation} J_2 = \frac{C-A}{Ma^2} = 1.082626\times 10^{-3} \label{eq10} \end{equation} 式 (9) の \(\omega^2a^3/GM\) は次のように変形すると， \[ \frac{\omega^2a^3}{GM} = \frac{\omega^2a}{\frac{GM}{a^2}}, \] 自転の遠心力と地球自身の重力（自己重力）の比であることが分かります．この比が１を超えると天体は破壊することになりますが，地球では 0.3% 程度で次の値を用いることが多いようです． \begin{equation} \frac{\omega^2a^3}{GM} = 3.46139\times 10^{-3} \label{eq11} \end{equation} 最後に， (10) と (11) の値を式 (9) に代入して次のように地球の扁平率が求まります． \begin{equation} f = 3.35463\times 10^{-3} = \frac{1}{298.095} \label{eq12} \end{equation}

↑ ページ冒頭

なお，専門レベルでは重力ポテンシャルをマッカラーの公式ではなく，球関数を用いてより高次の項まで展開し，精密な重力場を記述します．地球の扁平率もより精密に決定されることになります．

参考文献：

Stacey, F. D., Physics of the Earth (Third Edition), 513 pp., Brookfield Press, Brisbane, 1992.

→ ホーム