古地磁気学と岩石磁気学の基礎

恐竜の画像統計学的検定：共通の平均方向の検定； tmeandir

プログラム "tmeandir" はフィッシャー分布に従う単位ベクトルの２つ以上のグループが共通の平均方向を有するかを検定します．このプログラムは主に古地磁気方向の２つの分布の逆転テストに使用されますが，リバース方向は 180° 反転する必要があります．プログラムはまた，３つ以上のサイト平均古地磁気方向が共通の平均方向を有するかも検定します．

母集団の精密度パラメーターが等しい２つのグループ（\(\kappa_1=\kappa_2\)）

単位ベクトルの２つの分布を考えます．グループ１とグループ２のデータ数と合成ベクトルをそれぞれ， \(N_1\)， \(N_2\) と \({\bf R_1}\)， \({\bf R_2}\) で表し，全ての個々のベクトルの和については， \(N=N_1+N_2\) と \({\bf R=R_1+R_2}\) で表すことにします．ここで設定する帰無仮説は次の通りです．

H: ２つのグループの母集団は共通の平均方向を有する．

この帰無仮説のもとで， Watson (1956) は次の統計量， \[ F = (N-2)\frac{R_1 + R_2 - R}{N - R_1 - R_2}, \] が，母集団の精密度パラメーターが等しい場合，自由度 \(\nu_1\)=2 と \(\nu_2\)=2(\(N\)-2) の \(F\) 分布に従うことを示しました．有意水準を \(\alpha\) として，もし観測された \(F\) が上方 \(\alpha\) 点を超えたときは帰無仮説は棄却されます．この定理は大変難解な理論に基づいていますが，直感的な解釈は次の通りです．２つの平均方向があり，それぞれの誤差は小さいが角度差は大きいとすると，これらは共通の平均方向を有するとは考えられません．このような場合には， \(R_1+R_2\) は \(R\) よりずっと大きいが， \(N\) は \(R_1+R_2\) にかなり近いと考えられます．よって，統計量 \(F\) は大きくなり，有意水準に対応する値を超えることとなります．

上の理論は McFadden & Lowes (1981) により改良され，プログラム "tmeandir" は改良版を採用しています．即ち，２つの母集団の精密度パラメーターが等しい場合（\(\kappa_1=\kappa_2\)），次の統計量 \begin{equation} F = (N-2)\frac{R_1 + R_2 - R^2/(R_1 + R_2)}{2(N - R_1 - R_2)}, \label{eq01} \end{equation} は \(F\) 分布に従い，自由度は次式で与えられます． \begin{equation} \nu_1 = 2, \quad \nu_2 = 2(N - 2). \label{eq02} \end{equation} 観測された \(F\) が上方 \(\alpha\) 点 \(F_{\alpha,2,2(N-2)}\) を超えれば，共通の平均方向の帰無仮説は棄却されます． \({\bf R_1}\) と \({\bf R_2}\) の角度差 \(\gamma\) と \({\bf R}\) との関係式， \[ R^2 = R_1^2 + R_2^2 + 2 R_1 R_2 \cos\gamma, \] を利用して， \(F_{\alpha,2,2(N-2)}\) に対応する基準の角度差 \(\gamma_c\) は \eqref{eq01} から次のように求まります． \begin{equation} \cos\gamma_c = 1 - \frac{(N-R_1-R_2)(R_1+R_2)}{(N-2)R_1R_2}F_{\alpha,2,2(N-2)}. \label{eq03} \end{equation}

共通の平均方向の検定の前に，２つの母集団が共通の精密度パラメーターを有するかを検定する必要があります．帰無仮説 \(\kappa_1=\kappa_2\) のもとでは， \(\kappa_1\) と \(\kappa_2\) の最良推定値 \(k_1\) と \(k_2\) を用いて，次の統計量 \begin{equation} F = \frac{k_1}{k_2}, \label{eq04} \end{equation} は \(F\) 分布に従い，自由度は次式で与えられます． \begin{equation} \nu_1 = 2(N_2-1), \quad \nu_2 = 2(N_1-1). \label{eq05} \end{equation} 自由度 \(\nu_1\)， \(\nu_2\) とデータ数 \(N_1\)， \(N_2\) との関係が，前ページで示した分散の場合の逆で２倍となることに注意が必要です．実際の計算では， \(k_1\) と \(k_2\) の大きい方を \eqref{eq04} の分子に取り， \(F\) が常に１より大きくなるようにします（前ページの分散の検定と同様です）．もし観測から得られた統計量 \(F\) が上方 \(\alpha/2\) 点より小さければ， \(\kappa_1\) と \(\kappa_2\) は共通の \(\kappa\) と矛盾しないと考えて，上記の共通の平均方向の検定へ進みます．そうでないときは， \(\kappa\) が異なる場合の別の検定方法を採用します．

↑ ページ冒頭

共通の \(\kappa\) を要しない２つ以上のグループ

McFadden & Lowes (1981) は， \(\kappa\) が共通の３つのグループについて，平均方向が同一かどうかを検定する理論も導いています．このような場合には，プログラム "tmeandir" はこの方法を３つのグループに対して使用します．しかしここでは，その理論の説明は省略します．

２つ以上のグループの母集団 \(\kappa\) が同一でない場合には，プログラム "tmeandir" は G.S. Watson が 1983 年に提唱した別の方法を採用します．これは同一の \(\kappa\) を共有するかどうかとは関係なく，２つ以上のグループの検定に適用できます．この方法は， McFadden & McElhinny (1990) と Fisher et al. (1987) の p.211 に記述されています．

単位ベクトルの \(m\) 個のグループを考え， \(i\) 番目の \(N\)， \(k\)， \({\bf R}\) を \(N_i\)， \(k_i\)， \({\bf R_i}\) と記します（\(i=1,\cdots,m\)）．この方法で使用する統計量は，各合成ベクトルの絶対値の重み付き和 \(S_r\)， \[ S_r = k_1 R_1 + k_2 R_2 + \cdots + k_m R_m, \] と，次の各合成ベクトルの重み付きベクトル和 \({\bf R_w}\) です． \[ {\bf R_w} = k_1{\bf R_1} + k_2{\bf R_2} + \cdots + k_m{\bf R_m}. \] Watson は次の統計量， \begin{equation} V = 2(S_r - R_w), \label{eq06} \end{equation} が，全ての標本のサイズが大きい場合のみ（\(N_i ≥ 25\)），自由度が \(2(m-1)\) の \(\chi^2\) 分布で近似されることを示しました．しかし， McFadden & McElhinny (1990) で指摘されているように，この方法は計算機シミュレーションを使用すれば，小さな標本サイズにも適用可能です．そのため，プログラム "tmeandir" は式 \eqref{eq06} に基づいた計算機シミュレーションを，異なる \(\kappa\) の２または３グループ，および \(\kappa\) の同等性とは関係なく４以上のグループに対して使用しています．計算機シミュレーションは以下のように実行されます．

  1. 観測値 \(V_0\) を計算する．
  2. フィッシャー分布のランダム発生関数を使用して， \(N_i\) と \(k_i\) に対応する \(m\) 個の標本を作成し， \eqref{eq06} から \(V\) を計算する．
  3. \(V\) のシミュレーションを \(n\) 回繰り返し， \(V_j\) (\(j=1,\cdots,n\)) を得る．
  4. \(V_j\) を昇順にソートして， \(j\) が (\(n(1-\alpha)+1\)) を超えない最大の整数となる \(V_j\) を \(V\) の基準値 \(V_c\) とする．
  5. もし \(V_0\) が \(V_c\) を越えれば．共通の平均方向の帰無仮説を棄却する．

２グループの場合は，帰無仮説を棄却する基準となる平均方向の角度差 \(\gamma_c\) は次式で与えられます． \begin{equation} \cos\gamma_c = \frac{R_{wc}^2-(k_1R_{1c})^2-(k_2R_{2c})^2}{2k_1R_{1c}k_2R_{2c}}, \label{eq07} \end{equation} ここに， \begin{equation} R_{wc} = S_{rc} - V_c/2, \label{08} \end{equation} で， \(S_{rc}\)， \(R_{1c}\)， \(R_{2c}\) は \(V_c\) に対応する \(S_r\)， \(R_1\)， \(R_2\) のシミュレーションによる値です．もし観測による角度差 \(\gamma_0\) が \(\gamma_c\) を越えれば，共通の平均方向の帰無仮説は棄却されます．

↑ ページ冒頭

プログラムのダウンロードとインストール

→ このページにあります．

フィッシャー分布に従うランダムな単位ベクトルの発生方法

フィッシャー分布では，ベクトルを \(\theta\) と \(\theta + d\theta\) の間に見出す確率 \(f(\theta)d\theta\) は次式で表されます． \[ f(\theta)d\theta = \frac{\kappa}{2\sinh\kappa}e^{\kappa\cos\theta}\sin\theta d\theta. \] ０から１の値を取る一様乱数 \(x\) を用いて，フィッシャー分布に従う乱数 \(\theta\) を発生させるには，次の関係が成り立つ必要があります． \[ f(\theta)d\theta = dx, \] すなわち， \[ \frac{dx}{d\theta} = f(\theta). \] これを解くと， \[ x = \int_0^\theta f(\theta)d\theta = F(\theta) = \frac{1}{2\sinh(\kappa)}(e^\kappa - e^{\kappa\cos\theta}), \] ここに， \(F(\theta)\) は確率密度関数 \(f(\theta)\) の累積分布関数です．よって，乱数 \(\theta\) は下図のように \(F(\theta)\) の逆関数 \(F^{-1}(x)\) で与えられます．

フィッシャー分布に従う乱数 theta は累積分布関数 F(theta) の逆関数 F^-1(x) で与えられます．

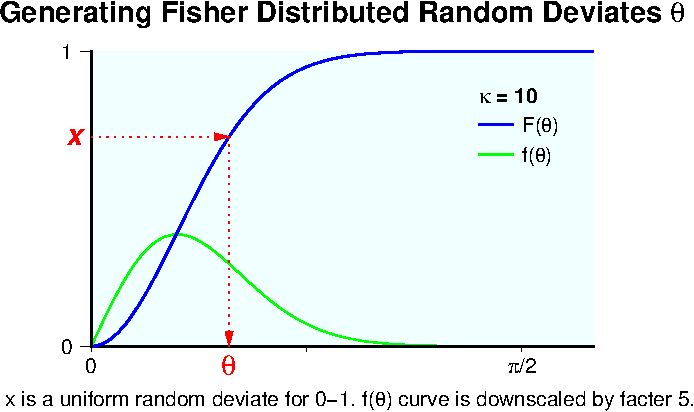
それ故，０から１の一様乱数 \(x_1\) と \(x_2\) を使用して，フィッシャー分布のランダム発生関数は，乱数 \(\varphi\) も含めて次の式で与えられます． \begin{eqnarray} \theta & = & \arccos\left( 1 + {1 \over \kappa}\log\left(1 - (1 - e^{-2\kappa})x_1\right) \right), \label{eq09} \\ \varphi & = & 2\pi x_2. \label{eq10} \end{eqnarray}

しかしながら，プログラム "tmeandir" は N.I. Fisher 他により 1981 年に開発された別の関数を使用しています（Fisher et al. 1987 の p.59 に記載）．このランダム発生関数は， \(\varphi\) については \eqref{eq10} と同じですが， \(\theta\) は次式で与えられます． \begin{equation} \theta = 2\arcsin\sqrt{ \frac{-\log(x_1(1-e^{-2\kappa})+e^{-2\kappa})}{2\kappa} }. \label{eq11} \end{equation} 式 \eqref{eq11} は解析的には，式 \eqref{eq09} で \(x_1\) を \(1-x_1\) で置き換えたものと同一です．しかし数値計算としては， \eqref{eq11} は特に小さな \(\kappa\) に対して \eqref{eq09} より優れているようです． McFadden & McElhinny (1990) によると，この関数が最も性能が良いようです．０から１の一様乱数 \(x\) については，プログラム "tmeandir" は Press et al. (1992) の関数 "ran1" を使用しています．

参考文献：

↑ ページ冒頭   ← 前ページ → 次ページ